Уравнение неразрывности. Графически движение жидкостей изображается с помощью линий тока, которые проводятся так, что касательные к ним совпадают по направлению с вектором скорости

Графически движение жидкостей изображается с помощью линий тока, которые проводятся так, что касательные к ним совпадают по направлению с вектором скорости жидкости в соответствующих точках пространства (рис. 1).

Густота линии тока, характеризуемая отношением числа линий к площади перпендикулярной им площадки, через которую они проходят, больше там, где больше скорость течения жидкости, и меньше там, где скорость меньше.

 

 

Рис.1. Линии тока Рис. 2. Трубка тока

Часть жидкости, ограниченную линиями тока, называют трубкой тока.

Течение жидкости называется установившимся (или стационарным), если форма и расположение линий тока, а также значения скоростей в каждой ее точке со временем не изменяются. Рассмотрим какую-либо трубку тока. Выберем два ее сечения и 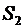, перпендикулярные направлению скорости (рис.2). Если жидкость несжимаема , то произведение скорости течения несжимаемой жидкости на поперечное сечение трубки тока является величиной постоянной для данной трубки тока (уравнение неразрывности для несжимаемой жидкости), т. е.

. Уравнение Бернулли

Для стационарно текущей идеальной жидкости (воображаемая жидкость, в которой отсутствуют силы внутреннего трения) трубка тока, ограниченная сечениями и 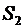, по которой слева направо течет жидкость, представлена на рисунке 3. В месте сечения − скорость течения 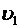, давление и высота, на которой это сечение расположено, .

Рис. 3. Трубка тока Аналогично, в месте сечения 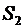скорость течения ,

Рис. 3 давление и высота сечения .

Для любого сечения трубки тока идеальной жидкости выполняется следующее условие: (уравнения Бернулли).

 

Из уравнения Бернулли и уравнения неразрывности следует:

1) при течении жидкости по горизонтальной трубе, имеющей различные сечения, скорость жидкости больше в местах сужения, а в широких местах скорость меньше;

2) выражение для скорости υ истечения жидкости из малого отверстия:

 

(формула Торричелли), где

- высота уровня воды над отверстием, - ускорение свободного падения.

 

Примеры решения задач по теме «Механика жидкости»

(Номера задач в скобках соответствуют сборнику задач по курсу физики Трофимовой Т.И.)

Задача №1 (1.214). В бочку заливается вода со скоростью 200 см³/с. На дне бочки образовалось отверстие площадью поперечного сечения 0,8 см. Пренебрегая вязкостью воды, определите уровень воды в бочке.

 

Дано: =200 см³=2*10^{-4 м3}, =1 с, = 0,8 см²=8*10^{-5 м2}.

Найти:

Решение:

Скорость истечения жидкости из малого отверстия по формуле Торричелли:

, где

- ускорение свободного падения,

- высота уровня воды в бочке над отверстием, которую можно выразить в

 

виде:

.

Для определения величины , учтем, что . Отсюда

 

тогда,

 

Подставим исходные данные в полученное выражение:

 

 

Ответ:.

Задача №2 (1.225). По горизонтальной трубе в направлении, указанном на рисунке 8 стрелкой, течет жидкость. Размер уровней жидкости в манометрических трубках 1 и 2 одинакового диаметра составляет 8 см. Определите скорость течения жидкости по трубе.

Дано: = 8 см = 8*10^-2м, .

Найти: -?

 

 

Решение:

Гидростатическое давление столба жидкости в манометрических трубках уравновешивается давлением в соответствующем месте трубы, чем и определяется высота столба жидкости в этих трубках. В трубке 1 с горизонтальным срезом высота столба жидкости определяется только статическим давлением, т.е. . Трубка Пито 2 имеет срез, позволяющий воде затекать в нее, поэтому высота столба жидкости в ней определяется суммой не только статического, но и динамического давления:

.

Следовательно, с одной стороны .

С другой стороны .

Таким образом, ,

,

В этих формулах - плотность жидкости, - ускорение свободного падения. Подставим исходные данные в полученное выражение:

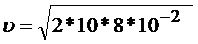= 1,25 м/с.

Ответ: = 1,25 м/с.

 

Задача №3 (1.229). Вдоль оси горизонтальной трубки диаметром 3 см, по которой течет углекислый газ, ( =7,5 кг/м³) установлена трубка Пито. Пренебрегая вязкостью, определите объем газа, проходящего за 1 секунду через сечение трубы, если разность уровней в жидкостном манометре составляет =0,5 см. Плотность жидкости принять равной =1000 кг/м³ .

Дано: =7.5 кг/м³, =1000 кг/м³, d =3 см =3*10^{-2 м, =0,5 см = 5*10-2}м,

t =1 c.

Найти:

 

 

Решение: Рис.

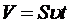Объем углекислого газа, протекающего за 1 секунду через сечение трубы:

Площадь поперечного сечения трубы равна . Разность уровней воды в трубке Пито обусловлена тем, что трубка 1 измеряет только статическое давление, а трубка 2 - сумму статического и динамического давления, следовательно (рис.).

С другой стороны , поэтому .

Скорость течения углекислого газа по трубе: .

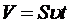Подставим выражения для величин и в выражение и получим

,

Подставим исходные данные в полученное выражение:

=2,25*10^{-3 м3}.

Ответ: = 2,25*10^{-3 м3}.

Задача №4 (1.231). Пренебрегая вязкостью жидкости, определите скорость истечения жидкости из малого отверстия в стенке сосуда, если высотауровня жидкости над отверстием составляет 1,5м.

Дано: h =1,5м.

Найти: -?

Рис.

 

Решение:

Запишем уравнение Бернулли и уравнение неразрывности для трубки тока с сечениями S₁ и S₂ в виде:

,

Так как (отверстие малое), то из уравнения неразрывности следует, что и скоростью по сравнению со скоростью истечения жидкости из отверстия можно пренебречь.

Следовательно, и уравнение Бернулли приобретает вид:

.

Отсюда скорость истечения жидкости из малого отверстия выражается в виде:

.

Подставим исходные данные в полученное выражение:

=5,42 м/с.

Ответ: =5,42 м/с.