Повышение температуры ускоряет все химические реакции. Первоначально Вант-Гофф экспериментально установил, что при увеличении температуры на каждые 10 градусов скорость возрастает в 2 ¸ 4 раза ( правило Вант-Гоффа ). Это соответствует степенной зависимости скорости от температуры:
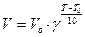 ,
,
где Т > Т0, g - температурный коэффициент Вант-Гоффа.
Однако это уравнение теоретически не обосновано;экспериментальные данные лучше описываются экспоненциальной функцией (уравнение Аррениуса):
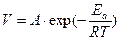 ,
,
где А - предэкспоненциальный множитель, не зависящий от Т, Еа - энергия активации химической реакции (кДж/моль), R - универсальная газовая постоянная.
Уравнение Аррениуса обычно записывают для константы скорости:
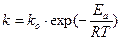 .
.
Это уравнение теоретически обосновывается методами статистической физики. Качественно это обоснование состоит в следующем: так как реакции идут в результате беспорядочных столкновений молекул, то эти столкновения характеризуются практически непрерывным набором энергий от самых маленьких до очень больших. Очевидно, что реакция произойдет только тогда, когда молекулы соударяются с энергией, достаточной для разрыва (или существенного растяжения) некоторых химических связей. Для каждой системы существует порог энергии Еа, начиная с которого энергия достаточна для протекания реакции, – этому механизму как раз и соответствует кривая 1 на рисунке 5.1. Так как соударения происходят с частотой, зависящей от температуры по экспоненциальному закону, то и получаются формулы 5.9 и 5.10. Тогда предэкспоненциальные множители А и k0 представляют некоторую характеристику полного числа столкновений, а член 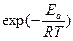 - долю результативных столкновений.
- долю результативных столкновений.
Анализ экспериментальных данных проводят, пользуясь логарифмической формой уравнения Аррениуса:
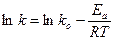 .
.
График строят в так называемых аррениусовских координатах
(ln k - 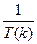 ),рис. 7.2; из графика находят ko и Еа.
),рис. 7.2; из графика находят ko и Еа.
При наличии экспериментальных данных для двух температур ko и Еа легко теоретически найти:
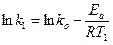 ;
; 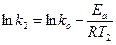 ;
;
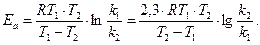
Скорость химической реакции в значительной мере зависит от энергии активации. Для подавляющего большинства реакций она лежит в пределах от 50 до 250 кДж/моль. Реакции, для которых
Еа > 150 кДж/моль, при комнатной температуре практически не протекают.
Пример 1. Сложная необратимая реакция 2N2O5 = 4NO2 + O2 является реакцией первого порядка. Как изменится ее скорость при увеличении давления в 5 раз?
Решение. Кинетическое уравнение этой реакции в общем виде: V = k·[N2O5]a. Так как реакция сложная, то возможно, что a ¹ 2. По условию порядок реакции
a = 1. Для газовых реакций роль концентрации выполняет давление. Поэтому
V = kP, и если Р1 = 5Р, то V1/V = 5, т.е. скорость возрастает в пять раз.
 ln k
ln k





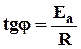

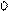
 ln ko
ln ko
 | |||
 | |||
 j
j


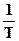
Рис. 5.2.Аррениусовская зависимость для константы скорости.
Точки – экспериментальные данные
Пример 2. Для реакции 2NO + H2 = N2O + H2O при 660 К измерена скорость при различных концентрациях NO и H2:
| NO, моль/л-1 | 0,01 | 0,01 | 0,03 |
| H2 моль/л-1 | 0,01 | 0,02 | 0,02 |
| V моль л-1 с-1 | 2,5.10-3 | 5.10-3 | 45.10-3 |
Найти константу скорости, порядки по реагентам и записать кинетическое уравнение.
Решение. Кинетическое уравнение для скорости этой реакции в общем виде:
V = k[NO]a[H2]b.
Данные таблицы позволяют найти порядки реакции по NO (a) и H2 (b) методом понижения порядка реакции, т.е. анализируя опыты, в которых один из реагентов имеет неизменную концентрацию. Так, [NO] = 0,01 в первом и втором столбцах, при этом [H2] изменяется.
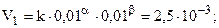

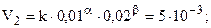
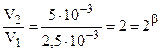 .
. 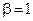 (частный порядок по H2).
(частный порядок по H2).
Для второго и третьего столбцов, наоборот, [H2] одинакова, а [NO] - различны, поэтому:
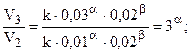
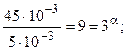
 (частный порядок по NO).
(частный порядок по NO).
Так как a и b совпадают со стехиометрическими коэффициентами, то реакция может быть простой. Константа скорости может быть найдена по данным каждого столбца:
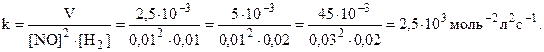
Таким образом, кинетическое уравнение: V = 2,5.103[NO]2[H2].
Суммарный (общий) порядок этой реакции (a + b) равен 3.
Пример 3. Скорость реакции А + 3В = АВ3 определяется кинетическим уравнением V = k[А]·[B]. Определите общий порядок реакции. Какая это реакция – простая или сложная? Во сколько раз увеличится скорость реакции при увеличении концентраций в 3 раза?
Решение. Порядок реакции определяется суммой показателей степеней реагентов в кинетическом уравнении. Для данной реакции общий порядок равен двум (1 +1).
Если бы данная реакция была простой, то по закону действующих масс
V = k[А]1.[B]3 и общий порядок был бы равен (1+ 3) = 4, т.е. показатели степеней в кинетическом уравнении не совпадают со стехиометрическими коэффициентами, следовательно, реакция сложная и проходит в несколько стадий.
При увеличении концентраций реагентов в 3 раза: V1 = k·3[A]·3[B] = 32V, то есть скорость увеличится в 32 = 9 раз.
Пример 4. Определить энергию активации реакции и ее температурный коэффициент, если при 398 и 600 0C константы скорости равны, соответственно, 2,1×10-4 и 6,25×10-1.
Решение. Еа по двум значениям может быть рассчитана по формуле 5.12:
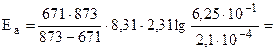 192б33 Дж/моль.
192б33 Дж/моль.
Температурный коэффициент находим из выражения (5.8), т.к. V µ k:
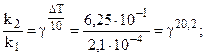
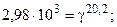
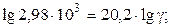
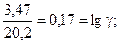
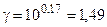 .
.
 2014-02-02
2014-02-02 3462
3462
