Тензор напряжений (или напряжённое состояние точки среды) зависит от скорости течения среды. Кинематическое соотношение, характеризующее движение жидкости, - это градиент скорости 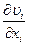 .
.
В общем случае течение, возможно, более чем одно ненулевое направление градиента скорости. Каждый из трёх компонентов скорости может изменяться в трёх координатных направлениях, что даёт девять возможных компонент градиента. Таким образом, можно ввести тензор градиентов скорости Ñu, который в декартовых координатах запишется:
 | Напряжённое состояние среды связано и определяется дифференциальными изменениями. Так, например, под воздействием одной и той же растягивающей силы различные материалы получают различные удлинения. Связь напряжений и деформаций для твёрдых тел осуществляется с помощью закона Гука: |
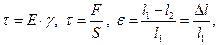 где
где
E – модуль упругости, физический смысл – напряжение.
Напряжения, их величина, в вязкой, жидкой среде связаны со скоростями течения среды.
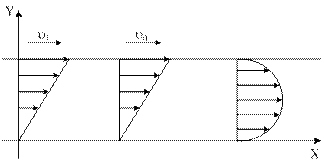 | Причём чем сильнее изменяется величина скорости по сечению канала, тем больше усилие действует на среду, тем большее напряжение в среде возникает: |
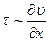 ; величина
; величина 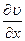 называется градиентом скорости.
называется градиентом скорости.
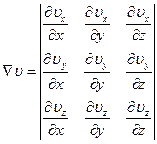
Движение жидкости представляет собой одновременное перемещение и вращение. Такие движения можно разделить, представить тензор градиентов деформацией в виде двух частей:
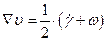
Где 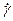 и
и 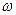 - тензор скоростей деформации и вращательный тензор.
- тензор скоростей деформации и вращательный тензор.
Тензор скоростей деформаций 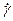 вводится следующим образом:
вводится следующим образом:
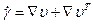 , где
, где
тензор 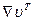 - транспонированный тензор, имеющий те же компоненты, что и Ñu, но с переставленными индексами (столбцы и строки переставлены).
- транспонированный тензор, имеющий те же компоненты, что и Ñu, но с переставленными индексами (столбцы и строки переставлены).
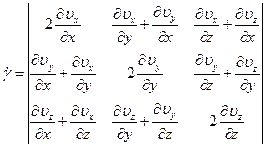
Уравнениями состояния или реологическими уравнениями называют уравнения связывающие тензор напряжений и тензор скоростей деформаций, т.е. 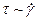
В том случае, если связь между этими тензорами линейна, то говорят, что жидкость является ньютоновской.
Если ньютоновская жидкость помещена между двумя параллельными, бесконечными пластинами и одна из пластин движется с постоянной скоростью, то после достижения установившегося течения, сила на единице площади, приводящая в движение пластину, пропорциональна скорости движения пластины и обратно пропорциональна расстоянию между пластинами.
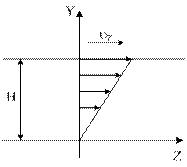 | 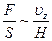 Выражение слева представляет собой напряжение, которое определяется как сила, действующая на единицу площади в плоскости с нормалью y и в направлении z, т.е. tyz. Далее так как профиль скорости линеен, то выражение справа представляет собой градиент скорости, т.е. Выражение слева представляет собой напряжение, которое определяется как сила, действующая на единицу площади в плоскости с нормалью y и в направлении z, т.е. tyz. Далее так как профиль скорости линеен, то выражение справа представляет собой градиент скорости, т.е. 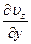 |
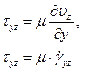 , где (2.1)
, где (2.1)
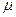 – коэффициент пропорциональности, вязкость*5 материала. Выражение (2.1) есть ньютоновский закон вязкости для несжимаемых жидкостей в простом сдвиговом течении.
– коэффициент пропорциональности, вязкость*5 материала. Выражение (2.1) есть ньютоновский закон вязкости для несжимаемых жидкостей в простом сдвиговом течении.
В общем случае ньютоновский закон течения:
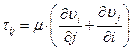 , или
, или
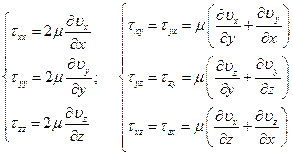 (2.2)
(2.2)
Неньютоновскими жидкостями называются все те жидкости, которые на различных основаниях не следуют ньютоновскому закону. В последние три десятилетия было применено много усилий для описания (создания) реологических законов, достаточно хорошо описывающих сложное поведение неньютоновских жидкостей.
Неньютоновский характер материала в теории экструзии и течении полимерных материалов в длинных трубах проявляются в нелинейной взаимосвязи напряжением сдвига и скорости сдвига.
Характер неньютоновской жидкости может быть проиллюстрирован следующим экспериментом. Представим длинную горизонтальную трубу длиной L и радиусом R, в которой скорость течения определяется как функция градиента давления. Тогда расход жидкости через поперечное сечение определяется:
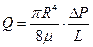
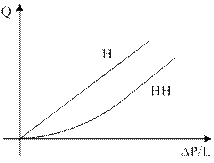 | Для неньютоновских жидкостей связь Q и 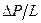 нелинейна. нелинейна. |
Все среды подразделяются на:
- ньютоновские;
- неньютоновские или аномально-вязкие;
А также подразделяются на:
- Вязкие;
- Вязко-упругие.
Аномально-вязкие среды подразделяются на:
1) псевдопластические;
2) дилатантные
К псевдопластическим средам относятся суспензии, содержащие асимметричные частицы, растворы и расплавы полимеров.
К дилатантным средам относятся суспензии с большим содержанием твёрдой фазы.
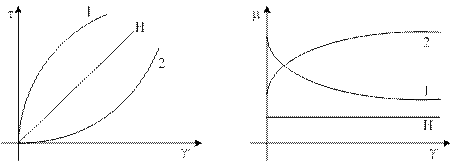
Математическое выражение связи напряжений и скоростей деформаций для ньютоновских жидкостей различны, многообразны и получены эмпирическим путём.
В кабельной промышленности, где для наложения полимеров, которые ведут себя как псевдопластические жидкости, наиболее распространённым реологическим законом является степенной закон. В общем случае закон течения для нелинейных сред:
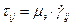 , где
, где
mэ – эффективная вязкость, вся нелинейность – в ней.
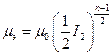 – реологический степенной закон, где
– реологический степенной закон, где
m0 – коэффициент консистенции или начальная вязкость;
I2 – второй инвариант тензора скоростей деформаций;
n – показатель аномалии.
Инвариант тензора – величина, не зависящая от выбора координат.
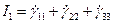 – первый инвариант тензора деформации;
– первый инвариант тензора деформации;
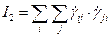 – второй инвариант тензора деформации.
– второй инвариант тензора деформации.
В декартовой системе координат I2 равен:
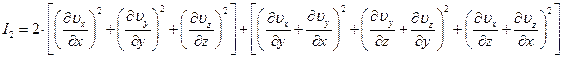
Кроме того, что вязкость может быть функцией скорости сдвига, для всех материалов характерна её температурная зависимость, всегда ниспадающая.
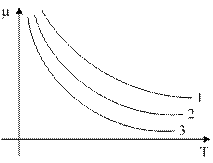 | 1, 2, 3 – материалы с разной молекулярной массой. Математически эта зависимость может быть представлена двумя различными выражениями: Уравнение Аррениуса: 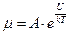 Уравнение Рейнольдса: Уравнение Рейнольдса: 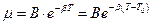 , где , где |
A, B – характеристики материала;
U (иногда пишут E) – энергия активации;
k – постоянная Больцмана;
T – температура;
b – температурный коэффициент.
С учётом зависимости 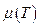 имеем реологическое уравнение:
имеем реологическое уравнение:
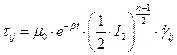
 2014-02-12
2014-02-12 3203
3203








