Задание 1
Решить приближенно методом итерации и методом Зейделя. Сравнить ответы.
Варианты задания:
1. 
| 14. 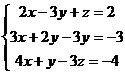
|
2. 
| 15. 
|
3. 
| 16. 
|
4. 
| 17. 
|
5. 
| 18. 
|
6. 
| 19. 
|
7. 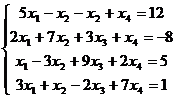
| 20. 
|
8. 
| 21. 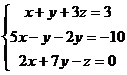
|
9. 
| 22. 
|
10. 
| 23. 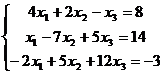
|
11. 
| 24. 
|
12. 
| 25. 
|
13. 
|
Примечание. Для лучшей сходимости итерационного процесса необходимо преобразовать уравнения, выделив наибольшие диагональные элементы при неизвестных. Для этого необходимо или переобозначить неизвестные (циклическая перестановка) или переставить уравнения.
Задание 2
Решить систему линейных уравнений  , заданную в матричной форме, методом итерации, предварительно найдя значения неизвестных одним из прямых методов.
, заданную в матричной форме, методом итерации, предварительно найдя значения неизвестных одним из прямых методов.
Варианты задания:
| Вариант | A | B |

| 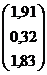
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 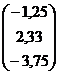
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 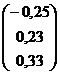
| |

| 
| |
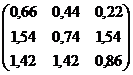
| 
| |

| 
| |
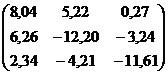
| 
| |

| 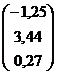
|
Задание 3
Найти все действительные корни уравнения 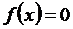 с точностью
с точностью  комбинированным методом и методом итерации. Сравнить число шагов, необходимое для достижения одинаковой точности этими методами. Вычисления вести с одним запасным знаком.
комбинированным методом и методом итерации. Сравнить число шагов, необходимое для достижения одинаковой точности этими методами. Вычисления вести с одним запасным знаком.
Варианты задания:
1. 
| 11. 
| 21. 
|
2. 
| 12. 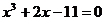
| 22. 
|
3. 
| 13. 
| 23. 
|
4. 
| 14. 
| 24. 
|
5. 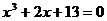
| 15. 
| 25. 
|
6. 
| 16. 
| 26. 
|
7. 
| 17. 
| 27. 
|
8. 
| 18. 
| 28. 
|
9. 
| 19. 
| 29. 
|
10. 
| 20. 
| 30. 
|
Задание 4
Построить кубическую сплайн-функцию для функции  , заданной таблично на отрезке
, заданной таблично на отрезке  .
.
Варианты задания:
| Вари-ант | Значения переменных | Перемен-ные | Значения переменных | Вари-ант | ||||||
| -1 | 
| |||||||||
| -3 | -1 | 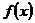
| -1 | -6 | ||||||

| -9 | -7 | -4 | -1 | ||||||
| -1 | 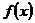
| -3 | -1 | |||||||

| ||||||||||
| -1 | -4 | 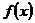
| -1 | -2 | ||||||

| -8 | -5 | ||||||||
| -2 | 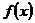
| -2 | -6 | |||||||
| -3 | -1 | 
| -7 | -5 | -4 | -1 | ||||
| -1 | 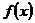
| -4 | ||||||||

| ||||||||||
| -3 | -7 | 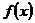
| -2 | |||||||
| -2 | -1 | 
| ||||||||
| -6 | 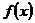
| -2 | ||||||||

| -4 | |||||||||
| -3 | -1 | 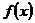
| -2 | -6 | ||||||
| -4 | -2 | 
| -3 | -1 | ||||||
| -1 | 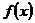
| -1 | -2 | |||||||
| -1 | 1,5 | 4,5 | 
| |||||||
| -7 | 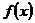
| -4 | -8 |
Задание 5
Вычислить приближенно  с точностью ε = 10- 3, воспользовавшись той из формул приближенного интегрирования, которая потребует меньшего объема вычислений. Вычислить определенный интеграл точно и сравнить с приближенным его значением.
с точностью ε = 10- 3, воспользовавшись той из формул приближенного интегрирования, которая потребует меньшего объема вычислений. Вычислить определенный интеграл точно и сравнить с приближенным его значением.
Варианты задания
| 1. | 
| 11. | 
| 21. | 
|
| 2. | 
| 12. | 
| 22. | 
|
| 3. | 
| 13. | 
| 23. | 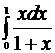
|
| 4. |  
| 14. | 
| 24. | 
|
| 5. | 
| 15. | 
| 25. | 
|
| 6. | 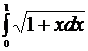
| 16. | 
| 26. | 
|
| 7. | 
| 17. | 
| 27. | 
|
| 8. | 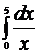
| 18. | 
| 28. | 
|
| 9. | 
| 19. | 
| 29. | 
|
| 10. | 
| 20. | 
| 30. | 
|
Задание 6
Численно решить дифференциальное уравнение у' = f (x,y) с начальным условием у 0 = у (х 0) на отрезке [ x 0, b ] с шагом h = 0,2 методом Эйлера, модифицированным методом Эйлера и методом Рунге-Кутта. Найти аналитическое решение у = у (х) заданного уравнения и сравнить значения точного и приближенных решений в точке x = b. Вычислить абсолютную и относительную погрешности в этой точке для каждого метода. Вычисления вести с четырьмя десятичными знаками.
Варианты задания
| 1. | 
| у (1)=1 | x  [1,2] [1,2]
|
| 2. | 
| у (0)=-1 | x  [0,1] [0,1]
|
| 3. | 
| у (1)=0 | x  [1,2] [1,2]
|
| 4. | 
| у (0)=-1 | x  [0,1] [0,1]
|
| 5. | 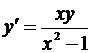
| у (2)=3 | x  [2,3] [2,3]
|
| 6. | 
| у (1)=0,5 | x  [1,2] [1,2]
|
| 7. | 
| у (1)=0 | x  [1,2] [1,2]
|
| 8. | 
| у (0)=1 | x  [0,1] [0,1]
|
| 9. | 
| у (1)=1 | x  [1,2] [1,2]
|
| 10. | 
| у (0)=1 | x  [0,1] [0,1]
|
| 11. | 
| у (1)=3 | x  [1,2] [1,2]
|
| 12. | 
| у (1)=0 | x  [1,2] [1,2]
|
| 13. | 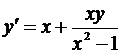
| у (2)=3 | x  [2,3] [2,3]
|
| 14. | 
| у (0)=1 | x  [0,1] [0,1]
|
| 15. | 
| у (1)=2 | x  [1,2] [1,2]
|
| 16. | 
| у (1)=2 | x  [1,2] [1,2]
|
| 17. | 
| у (0)=3 | x  [0,1] [0,1]
|
| 18. | 
| у (0)=0,5 | x  [0,1] [0,1]
|
| 19. | 
| у (1)=1 | x  [1,2] [1,2]
|
| 20. | 
| у (1)=1 | x  [1,2] [1,2]
|
| 21. | 
| у (1)=4 | x  [1,2] [1,2]
|
| 22. | 
| у (1)=3 | x  [1,2] [1,2]
|
| 23. | 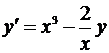
| у (1)=-5/6 | x  [1,2] [1,2]
|
| 24. | 
| у (2)=4 | x  [2,3] [2,3]
|
| 25. | 
| у (1)=1 | x  [1,2] [1,2]
|
| 26. | 
| у (1)=0 | x  [1,2] [1,2]
|
| 27. | 
| у (1)=1 | x  [1,2] [1,2]
|
| 28. | 
| у (1)=1 | x  [1,2] [1,2]
|
| 29. | 
| у (1)=1 | x  [1,2] [1,2]
|
| 30. | 
| у (1)=0,5 | x  [1,2] [1,2]
|
Задание 7
Методом Рунге-Кутта найти с точностью до ε = 10-3 решение дифференциального уравнения у = f (x,y) с начальным условием у (0) = 0 на отрезке [0;0,2].
Варианты задания
| 1. | 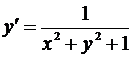
| 16. | 
|
| 2. | 
| 17. | 
|
| 3. | 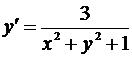
| 18. | 
|
| 4. | 
| 19. | 
|
| 5. | 
| 20. | 
|
| 6. | 
| 21. | 
|
| 7. | 
| 22. | 
|
| 8. | 
| 23. | 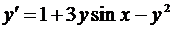
|
| 9. | 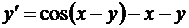
| 24. | 
|
| 10. | 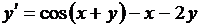
| 25. | 
|
| 11. | 
| 26. | 
|
| 12. | 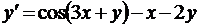
| 27. | 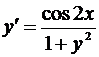
|
| 13. | 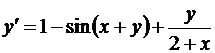
| 28. | 
|
| 14. | 
| 29. | 
|
| 15. | 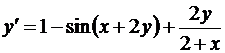
| 30. | 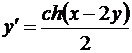
|
Задание 8
Методом Рунге-Кутта найти решение дифференциального уравнения y'' = f (x, y, z) c начальными условиями у (х 0) = у 0,  на отрезке [0;0,3] и с шагом h = 0,1. Найти аналитическое решение у (х) = у заданного уравнения и составить таблицу точного и приближенного решений заданного уравнения во всех точках х 1, х 2, х 3. Все вычисления вести с шестью десятичными знаками.
на отрезке [0;0,3] и с шагом h = 0,1. Найти аналитическое решение у (х) = у заданного уравнения и составить таблицу точного и приближенного решений заданного уравнения во всех точках х 1, х 2, х 3. Все вычисления вести с шестью десятичными знаками.
Варианты задания
| 1. | 
| у (0)=1 |  (0)=1 (0)=1
|
| 2. | 
| у (0)=1 |  (0)=2 (0)=2
|
| 3. | 
| у (0)=1 |  (0)=2 (0)=2
|
| 4. | 
| у (0)=1 |  (0)=-2 (0)=-2
|
| 5. | 
| у (0)=1 |  (0)=-1 (0)=-1
|
| 6. | 
| у (0)=1 |  (0)=3 (0)=3
|
| 7. | 
| у (0)=5 |  (0)=0,5 (0)=0,5
|
| 8. | 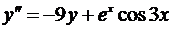
| у (0)=1 |  (0)=2 (0)=2
|
| 9. | 
| у (0)=-1 |  (0)=1 (0)=1
|
| 10. | 
| у (0)=1 |  (0)=2 (0)=2
|
| 11. | 
| у (0)=1 |  (0)=1 (0)=1
|
| 12. | 
| у (0)=1 |  (0)=-1 (0)=-1
|
| 13. | 
| у (0)=1 |  (0)=-1 (0)=-1
|
| 14. | 
| у (0)=1 |  (0)=1 (0)=1
|
| 15. | 
| у (0)=1 |  (0)=-1 (0)=-1
|
| 16. | 
| у (0)=2 |  (0)=1 (0)=1
|
| 17. | 
| у (0)=1 |  (0)=2 (0)=2
|
| 18. | 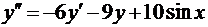
| у (0)=1 |  (0)=-1 (0)=-1
|
| 19. | 
| у (0)=1 |  (0)=2 (0)=2
|
| 20. | 
| у (0)=1 |  (0)=-2 (0)=-2
|
| 21. | 
| у (0)=1 |  (0)=-1 (0)=-1
|
| 22. | 
| у (0)=0 |  (0)=0,5 (0)=0,5
|
| 23. | 
| у (0)=1 |  (0)=-1,5 (0)=-1,5
|
| 24. | 
| у (0)=2 |  (0)=1 (0)=1
|
| 25. | 
| у (0)=-7 |  (0)=0 (0)=0
|
| 26. | 
| у (0)=4 |  (0)=-1 (0)=-1
|
| 27. | 
| у (0)=3 |  (0)=1 (0)=1
|
| 28. | 
| у (0)=-2 |  (0)=1 (0)=1
|
| 29. | 
| у (0)=3 |  (0)=2 (0)=2
|
| 30. | 
| у (0)=1 |  (0)=3 (0)=3
|
 2017-12-14
2017-12-14 553
553








