Электростатическое поле - поле потенциальное

Составим выражение для разности потенциалов в поле точечного заряда. С этой целью положим, что в точке m(рис. 11.2.) находится положительный точечный заряд q₁, создающий поле, а из точки 1 в точку 2 через промежуточную точку 3 перемещается единичный положительный заряд q=1.

Обозначим: R₁ — расстояние от точки m до исходной точки 1, R₂ — расстояние от точки m до конечной точки 2, R —расстояние от точки m до произвольной точки 3 на пути 132. Направление напряженности поля Е и направление элемента пути dl в промежуточной точке 3 показано на рис. 11.2. Скалярное произведение Edl=EdR, где dR есть проекция элемента пути dl на направление радиуса, соединяющего точку m с точкой 3. В соответствии с определением, напряженность поля

.

По закону Кулона

.

Так как \R₀\= 1 и q = 1, то модуль напряженности поля в поле точечного заряда q₁ равен

Подставим в формулу (11.2) вместо Edl величину dR. Получим

. (11.3)

Таким образом, разность потенциалов между исходной и конечной точками пути (точками 1 и 2) зависит только от положения этих точек и не зависит от пути, по которому происходило перемещение из исходной точки в конечную точку.

Другими словами, если перемещение из точки 1 в точку 2 будет происходить по какому-то другому пути, например, по пути 142, то разность потенциалов j₁ - j₂, полученная в этом случае, будет в точности равна разности потенциалов j₁ - j₂ при перемещении из точки 1 в точку 2 по пути 132. Если поле создано совокупностью точечных зарядов, то проделанный выше вывод справедлив для поля, созданного каждым из точечных зарядов в отдельности. А так как для электрического поля в однородном и изотропном диэлектрике справедлив принцип наложения, то вывод о независимости величины разности потенциалов j₁ - j₂ от пути, по которому происходило перемещение из точки 1 в точку 2, справедлив и для электрического поля, созданного совокупностью точечных зарядов. Если пройти по замкнутому пути 13241 (рис. 11.2), то исходная точка пути (1) и конечная точка пути (1) совпадут, и тогда и левая и правая части формулы (11.2) будут равны нулю

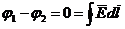. (11.4) Кружок на знаке интеграла свидетельствует о том, что интеграл берется по замкнутому контуру.

Соотношение (11.4) означает, что в электростатическом поле линейный интеграл от напряженности электрического поля, взятый вдоль любого замкнутого пути, равен нулю.

Физически это объясняется тем, что при движении вдоль замкнутого пути совершена определенная работа силами поля и такая же работа совершена внешними силами против сил поля.

Если условиться работу, совершенную силами поля, считать положительной, а работу, совершенную против сил поля, отрицательной, то сумма «положительных» и «отрицательных» работ равна нулю.

Выражение (11.4) можно трактовать и так: циркуляция вектора Е вдоль любого замкнутого контура равна нулю. Это соотношение выражает собой основное свойство электростатического поля. Поля, для которых выполняются подобного рода соотношения, называются потенциальными. Потенциальными являются не только электростатические поля, но и все гравитационные поля (поля сил тяготения между материальными телами), установившиеся температурные поля около нагретых тел и т. д.