Выражение напряженности в виде градиента от потенциала

Как уже говорилось, электростатическое поле является полем потенциальным. Между двумя близко расположенными точками поля имеется в общем случае некоторая разность потенциалов.

Если эту разность поделить на кратчайшее расстояние между взятыми точками, то полученная величина будет характеризовать скорость изменения потенциала в направлении кратчайшего расстояния между точками. Эта скорость будет зависеть от направления, вдоль которого взяты точки. В курсе математики пользуются понятием градиента скалярной функции. Под градиентом скалярной функции понимают скорость изменения скалярной функции, взятую в направлении ее наибольшего возрастания. В этом определении градиента существенны два положения. Первое то, что направление, в котором берутся две близлежащие точки, должно быть таким, что скорость изменения потенциала максимальна. Второе то, что направление это таково, что скалярная функция в этом направлении возрастает (не убывает). На рис. 11.3, б изображены отрезки двух весьма близкорасположенных эквипотенциалей. Одна из них имеет потенциал j₁, другая—j₂. Пусть j₁ > j₂. Тогда, в соответствии с приведенным определением градиента потенциала, последний изобразится на рис. 11.3. б вектором, перпендикулярным к эквипотенциальным линиям и направленным от j₂ к j₁ (в сторону увеличения потенциала). Напряженность электрического поля направлена от более высокого потенциала (j₁) к более низкому (j₂). Если расстояние по перпендикуляру (по нормали) между эквипотенциальными поверхностями обозначить dn и через dn обозначить вектор, совпадающий с направлением Е,

.

(здесь `n ° — единичный вектор по направлению dn), то тогда можно на основании соотношения (11.2) записать выражение:

,

где через d j = j₂ — j₁ обозначено приращение потенциала при переходе от точки 1 к точке 2.

Так как векторы Ē и dn совпадают по направлению, то скалярное произведение Ē dn равно произведению модуля Е на модуль

dn(`Edn= Edn).

Таким образом, Edn = - d j. Отсюда модуль напряженности поля Е= 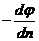. Вектор напряженности поля Е = Е `n °. Следовательно,

(11.5)

В свою очередь из определения градиента следует, что

. (11.6)

Сопоставляя (11.5) и (11.6), замечаем, что

. (11.7)

Соотношение (11.7) может быть истолковано следующим образом: напряженность в какой-либо точке поля равна скорости изменения потенциала в этой точке поля, взятой с обратным знаком. Знак минус имеет вполне определенный смысл: направление Е и направление gradj противоположны (рис. 11.3б).

Нормаль dn в общем случае может быть расположена таким образом, что не совпадет с направлением какой-либо координатной оси. И потому градиент потенциала в общем случае может быть представлен в виде суммы трех проекций по координатным осям. Например, в декартовой системе координат

, (11.8)

где - представляет собой скорость изменения j в направлении оси х, —есть числовое значение (модуль) скорости (скорость-величина векторная), i, j, k — единичные орты, соответственно, по осям х, у, z декартовой системы.

В свою очередь, вектор напряженности Ē = Е + Е_y + Е_z.

Таким образом,

.

Два вектора равны друг другу только тогда, когда равны друг другу соответствующие проекции их. Следовательно,

; ; . (11.9)

Соотношения (11.9) следует понимать так: проекция напряженности поля на ось х равна проекции скорости изменения потенциала вдоль оси х, взятой с обратным знаком, и т. д.

Для сокращения записи различных операций над скалярными и векторными величинами употребляется дифференциальный оператор Гамильтона (оператор набла).