Та у стані рівноваги (б)

Із встановленням стану рівноваги рівень Фермі в обох областях встановлюється на однаковому енергетичному рівні, і це супроводжується викривленням енергетичних зон (рис.2б). Між областями виникає контактна різниця потенціалів 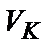, яка утворює в – переході потенціальний бар’єр , який забороняє перехід електронів з – області в – область (для дірок навпаки, з – області в – область).

Як показують розрахунки, висота потенціального бар’єру встановлюється таким чином, що концентрації електронів і дірок на межах шару підпорядковані статистиці Больцмана, тобто

, .

Звідси

. (4)

Із (4) можна бачити, що потенціальний бар’єр тим вищий, чим більше відношення концентрації основних носіїв заряду в даній області напівпровідника до концентрації цих носіїв в іншій області, де вони не є основними. При 10²² м^-3, 10¹⁶ м^-3 і К, його висота становить 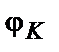=0,45 еВ.

Шар об’ємного заряду, що виникає на межі областей, розповсюджується на глибину в – область і на глибину в –область. Товщина шару об’ємного заряду визначається висотою потенціального бар’єру та концентраціями основних носіїв заряду у відповідних областях

, (5)

де 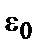=8,85×10^-12 Ф/м – діелектрична стала вакууму, – діелектрична проникність речовини, і може досягати значень 10^-6…10^-4 см.

Із рівності потоків носіїв заряду (3) випливає, що у стані рівноваги струм через – перехід не протікає. Позначимо густину струму, що відповідає потоку через , потоку – через , потоку – через , потоку – через 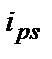. На рис.2б ці потоки вказані стрілками. У відповідності із (3) можна записпти

, . (6)

Додаючи ліві і праві частини цих рівностей, маємо

Ліва частина рівності являє собою повний струм , що протікає у –переході, а отже

. (7)

Рівність (7) виражає умову відсутності струму у –переході у стані рівноваги. Знайдемо та 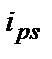. Для цього виділимо на границі –переходу з боку – області одиничну площадку і побудуємо на ній циліндр із твірною (рис.3), де 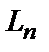– дифузійна довжина електронів в – області, – середній час їх життя у ній.

Рис.3. Ілюстрація для розрахунку густин струмів неосновних носіїв заряду

Зауваження. Вважається, що опір –переходу великий у порівнянні із опорами кожної з областей, тобто за межами –переходу носії заряду рухаються лише внаслідок дифузії. За час свого життя вони в середньому зміщуються на відстань , яка називається дифузійною довжиною. Розрахунок показує, що

де – коефіцієнт дифузії носіїв заряду, пов’язаний з їх рухливістю 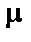співвідношенням Ейнштейна

Таким чином, величина являє собою середню швидкість дифузії електронів з глибини – області, де їхня концентрація становить 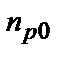, до границі –переходу, де вони підхоплюються контактним полем і перекидаються до – області.

Кількість електронів у виділеному циліндрі визначається як добуток об’єму циліндра на концентрацію електронів у –області , тобто . Всі ці електрони за 1 с пройдуть через одиничну площадку і будуть перекинуті до – області, створивши струм густиною

. (8)

Аналогічно можна знайти 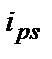, побудувавши циліндр з одиничною основою і твірною на межі –переходу з – областю,

. (9)

Таким чином, у стані рівноваги

(10)

перехід за наявності зовнішньої напруги

Оскільки область –переходу має найбільший опір, прикладена зовнішня напруга падає переважно на ньому, і саме його властивості визначають умови протікання струму через кристал.

Прямий струм. Прикладемо до –переходу, який знаходиться у стані рівноваги (рис.4а), зовнішню різницю потенціалів у прямому напрямку, тобто підключивши до – області позитивний полюс джерела живлення, а до – області – негативний (рис.4б). Ця різниця потенціалів викличе зниження висоти потенціального бар’єра до . Внаслідок цього потоки та збільшаться у разів, що приведе до збільшення у разів густин струмів основних носіїв заряду

(11)

Натомість густини струмів неосновних носіїв заряду та 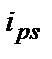, величина яких не залежить від висоти потенціального бар’єру –переходу, залишаться без змін і будуть виражатися формулами (10).

Таким чином, повний струм , що протікає у – переході в прямому напрямку буде відмінний від нуля і становитиме

. (12)

Рис.4. Енергетична схема – переходу у стані рівноваги (а), при прямому (б) та зворотному (в) включенні.

Зворотний струм. Тепер прикладемо до –переходу, зовнішню різницю потенціалів у зворотному напрямку, тобто підключивши до – області негативний полюс джерела живлення, а до – області – позитивний (рис.4в). Ця різниця потенціалів викличе підвищення висоти потенціального бар’єра до , що приведе до зменшення у разів густин струмів основних носіїв заряду

(13)

Тоді густина повного зворотного струму через – перехід

. (14)

Вольт-амперна характеристика переходу

Об’єднавши вирази (12) і (14), отримаємо

, (15)

де , знак “+” відноситься до прямого напрямку включення – переходу, а знак “-“ – до зворотного. Співвідношення (15) являє собою рівняння вольт-амперної характеристики (ВАХ) – переходу, яке виражає кількісний зв’язок між густиною струму, що протікає через перехід, і різницею потенціалів, прикладеною до нього.

Проаналізуємо отриманий вираз. При прикладанні зовнішньої напруги у зворотньому напрямку із її збільшенням експонента у формулі (15) прямує до нуля, а . Абсолютну величину

(16)

називають густиною струму насичення. Практично це досягається при 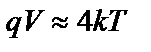, тобто при напругах 0,1 В, оскільки при кімнатних температурах 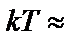0,025 еВ. Із (16) видно, що струм насичення визначається потоком через – перехід неосновних носіїв заряду та . Оскільки їх концентація невисока, то є невеликою величиною. Для германієвих – переходів ~10^-2 А/м², для кремнієвих це значення ще менше.

Згідно (15), при прикладанні зовнішньої напруги 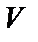в прямому напрямку струм через – перехід зростає експоненціально, набагато перевищуючи зворотній струм. Наприклад, для 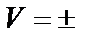0,5 В

Таким чином, – перехід має яскраво виражену однобічну (уніполярну) провідність, демонструючи високі випрямлюючі властивості, що використовується у діодах (рис.5).