
|



|



|



|

|


Короткий довідник з теми «Диференціальні рівняння I порядку»
| Тип рівняння | Стандартна форма запису | Особливості | Метод розв’язування |
| З відокремлюючими змінними | 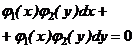
| При диференціалах – похідна функції, яка залежить одна від x, інша – від y | 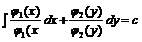
|

| Права частина – добуток функцій, які залежать одна від x, інша – від y | 
| |
| Однорідне | 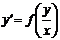
| Права частина – однорідна функція нульового порядку | 
|

|  - однорідні функції однакового порядку - однорідні функції однакового порядку
| 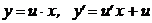
| |
| В повних диференціалах | 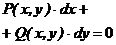
| 
|  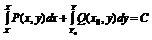
|
| Лінійне | 
| Першої степіні відносно 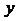 та та 
| 
|

|
Першої степіні відносно  та та 
| 
| |
| Бернуллі | 
| Відрізняється від лінійного правою частиною | Аналогічно лінійним |
Розробка лекцій до змістовного модуля І
Лекція 1
Тема: «Диференціальні рівняння, основні визначення»
Мета:
– вивчення основних положень та визначень з теми «Диференціальні рівняння»;
– ознайомлення із виникненням та застосуванням диференціальних рівнянь;
– поглиблення, розширення знань, отриманих раніше при вивченні розділів диференціального і інтегрального числення з курсу математичного аналізу, алгебри та геометрії.
– розвиток наукового мислення та пам’яті;
– виховання культури математичного запису і мовлення.
При вивченні теми студенти повинні:
знати: означення диференціального рівняння та основні поняття, які його стосуються (види, порядок, степінь, розв'язок);
уміти: визначати диференціальне рівняння з переліку рівнянь, складати рівняння за умовою задачі, що приводить до диференціального рівняння;
здатні: знаходити невизначений інтеграл (з курсу математичного аналізу).
Основні поняття: диференціальне рівняння (ДР), звичайне ДР, ДР у частинних похідних, порядок ДР, степінь, розв'язок.
Обладнання: підручники, дидактичний матеріал (таблиці), креслярські матеріали, мультимедійний проектор, комп’ютер.
Час: 2 год.
План лекції
1. Поняття диференціального рівняння і його розв'язку.
2. Приклади задач, які приводять до диференціального рівняння.
Список літератури
1. Еругин Р.П. и др. Курс обыкновенных дифференциальных уравнений.
2. Пономарев К.К. Составление дифференциальных уравнений.
3. Pudy A.E., Rakov S.A. Mathematical Analysis. Differential Equations.
4. Давидов М.О. Курс математичного аналізу: Підручник: У 3 ч. Ч. 2. Функції багатьох змінних і диференціальні рівняння. – 2-ге вид., перероб. і допов. – К.: Вища школа, 1991 – 336 с.
Текст лекції
1.Поняття диференціального рівняння і його розв'язку.
В диференціальному численні за заданою функцією одного чи більшого числа змінних вивчались властивості цієї функції (монотонність, випуклість і ін.). Однак більшість задач практичного застосування мають характер обернених: треба знайти функцію, яка б мала наперед задані властивості.
При вивченні фізичних явищ часто не вдається безпосередньо знайти закон, який зв’язує розглядувані величини, але в той же час порівняно легко встановлюється залежність між тими ж величинами і їх похідними або диференціалами.
І ті і другі задачі приводять до рівнянь, що містять невідомі функції під знаками похідних і диференціалів.
Означення 1. Рівняння, в яких невідома функція входить під знаком похідної або диференціала, називаються диференціальними рівняннями. Наприклад, диференціальними рівняннями є такі:




Означення 2. Якщо в диференціальному рівнянні невідома функція є функцією однієї незалежної змінної, то таке диференціальне рівняння називається звичайним.
У загальному випадку його можна записати у вигляді
 (1)
(1)
де  - незалежна змінна,
- незалежна змінна, 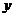 - функція від
- функція від  , яка підлягає визначенню,
, яка підлягає визначенню,  - її похідні.
- її похідні.
Означення 3. Якщо невідома функція, яка входить у диференціальне рівняння, є функцією двох і більшого числа незалежних змінних, то таке диференціальне рівняння називається рівнянням у частинних похідних.
Рівняння 1), 2) і 4) є звичайними диференціальними рівняннями, а 3) – рівняння в частинних похідних.
Означення 4. Порядком диференціального рівняння називається максимальний порядок похідної (або диференціала), що входить у нього.
Рівняння 1) і 4) є рівняннями першого порядку. Рівняння (1) – звичайне диференціальне рівняння  ого порядку.
ого порядку.
Означення 5. Якщо ліва частина рівняння (1) є многочленом відносно похідної максимального порядку від невідомої функції, то степінь цього многочлена називається степенем даного диференціального рівняння. Наприклад, рівняння

- п’ятого степеня другого порядку, а рівняння
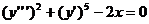
- другого степеня третього порядку.
У диференціальному рівнянню (1)  ого порядку незалежна змінна
ого порядку незалежна змінна  , шукана функція
, шукана функція  і її похідні до
і її похідні до  ого порядку включно в явному вигляді можуть бути, але можуть окремо або всі разом бути відсутніми. Наявність же в явному вигляді похідної
ого порядку включно в явному вигляді можуть бути, але можуть окремо або всі разом бути відсутніми. Наявність же в явному вигляді похідної  ого порядку необхідна, щоб це рівняння було диференціальним. Наприклад,
ого порядку необхідна, щоб це рівняння було диференціальним. Наприклад, 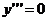 є диференціальним рівнянням третього порядку, хоча в ньому в явному вигляді й відсутні
є диференціальним рівнянням третього порядку, хоча в ньому в явному вигляді й відсутні  і
і  .
.
Означення 6. Розв’язком диференціального рівняння (1) називається  разів диференційована функція
разів диференційована функція 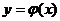 в інтервалі
в інтервалі  , яка, будучи підставленою в це рівняння, перетворює його в інтервалі
, яка, будучи підставленою в це рівняння, перетворює його в інтервалі  в тотожність
в тотожність
 .
.
Наприклад, функція  є розв’язком рівняння
є розв’язком рівняння

оскільки для всіх 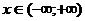 вона перетворює це рівняння в тотожність.
вона перетворює це рівняння в тотожність.
Справді, знайшовши похідні 
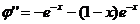 і підставивши функцію
і підставивши функцію  її похідні в рівняння, дістанемо тотожність
її похідні в рівняння, дістанемо тотожність
 ,
,
правильну для  .
.
Розв’язати диференціальне рівняння – означає знайти всі його розв'язки. Ці розв'язки найчастіше приводять до обчислення невизначених інтегралів. Тому операція знаходження розв’язків диференціального рівняння називається інтегруванням цього рівняння. Задача інтегрування диференціального рівняння вважається розв’язаною, якщо цю задачу звести до більш простої і вже вивченої в курсі інтегрального числення задачі обчислення невизначених інтегралів.
2. Приклади задач, які приводять до диференціального рівняння.
Задача 1. Знайти криві, які мають ту властивість, що відрізок дотичної (проведеної в будь-якій її точці), який міститься між осями координат, ділиться точкою дотику навпіл.
Розв’язання. Нехай  - довільна точка шуканої кривої
- довільна точка шуканої кривої 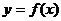 (мал. 1). Тоді
(мал. 1). Тоді  . Оскільки
. Оскільки  ,
,  то маємо співвідношення
то маємо співвідношення
 (2)
(2)


Мал. 1. Мал. 2.
яке зв’язує незалежну змінну  , шукану функцію
, шукану функцію  і її похідну
і її похідну 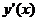 , тобто дістали звичайне диференціальне рівняння першого порядку. Переписавши (2) у вигляді
, тобто дістали звичайне диференціальне рівняння першого порядку. Переписавши (2) у вигляді  , а це останнє – у вигляді
, а це останнє – у вигляді  ,
,
маємо рівність  . Звідси
. Звідси  , і, отже,
, і, отже,
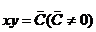 , (3)
, (3)
де  . Шукані криві (3) є сім'єю гіпербол, для яких осі координат виконають роль асимптот.
. Шукані криві (3) є сім'єю гіпербол, для яких осі координат виконають роль асимптот.
Задача 2. Відомо, що швидкість розпаду радію пропорційна наявній його кількості.
Знайти закон, який виражає зміну кількості радію протягом часу, якщо відомо, що через 1600 років залишиться половина кількості радію.
Розв’язання. Нехай  - кількість радію в момент часу
- кількість радію в момент часу  (час у роках). Оскільки швидкість зміни є похідною від
(час у роках). Оскільки швидкість зміни є похідною від  за часом
за часом  , то, згідно з умовою задачі,
, то, згідно з умовою задачі,
 . (4)
. (4)
Тут задача привела до звичайного диференціального рівняння першого порядку.
Переписавши (4) у вигляді 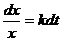 . А останнє у вигляді
. А останнє у вигляді 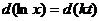 , маємо рівність
, маємо рівність
 , (5)
, (5)
де  - стала.
- стала.
Нехай у початковий момент 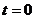 кількість радію дорівнює
кількість радію дорівнює  . Підставляючи замість
. Підставляючи замість  і
і  в (5) відповідно
в (5) відповідно  і
і  , дістанемо
, дістанемо  . Таким чином,
. Таким чином,  або
або  .
.
Коефіцієнт  знаходимо з умови, що
знаходимо з умови, що  при
при 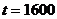 :
:

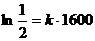 .
.
Звідси  .
.
Отже, кількість радію в момент часу  визначається за формулою
визначається за формулою
 .
.
Задача 3. З циліндричної посудини висотою  і радіусом
і радіусом 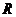 , повністю заповненою водою, через отвір площі
, повністю заповненою водою, через отвір площі  , що міститься в його дні, витікає вода. За яким законом буде знижуватися рівень води в посудині протягом часу, якщо відомо, що швидкість
, що міститься в його дні, витікає вода. За яким законом буде знижуватися рівень води в посудині протягом часу, якщо відомо, що швидкість  витікання рідини з отвору залежить від висоти
витікання рідини з отвору залежить від висоти  (Мал.3) стовпа рідини за формулою
(Мал.3) стовпа рідини за формулою
 ,
,
де  - прискорення вільного падіння.
- прискорення вільного падіння.
Розв’язання. За проміжок часу від  до
до  висота рівня води в посудині знизиться з висоти
висота рівня води в посудині знизиться з висоти  до
до  . За цей час
. За цей час  з посудини витікає об’єм води, що дорівнює –
з посудини витікає об’єм води, що дорівнює –  . Такий же об’єм води витікає з отвору. Він дорівнює
. Такий же об’єм води витікає з отвору. Він дорівнює 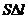 , де
, де  - довжина шляху, пройденого частинкою рідини з моменту
- довжина шляху, пройденого частинкою рідини з моменту  до
до  :
:  , де
, де  - середня швидкість руху рідини за час
- середня швидкість руху рідини за час  .
.
Таким чином,
 ,
,
звідси  ; де
; де  .
.
Переходячи до границі при  , дістанемо диференціальне рівняння
, дістанемо диференціальне рівняння
 ,
,
яке зв’язує  і
і  .
.
З (6) маємо
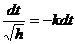 або
або 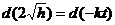 .
.
Звідси  , де
, де  - довільна стала. Оскільки в момент
- довільна стала. Оскільки в момент 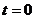 рівень
рівень  , то
, то  . Отже,
. Отже, 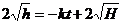 або
або  . Такий закон витікання рідини з отвору в дна посудини. Взявши
. Такий закон витікання рідини з отвору в дна посудини. Взявши  , дістанемо
, дістанемо

- час, протягом якого з посудини витікає вся рідина.
Лекція 2
Тема: «Диференціальні рівняння першого порядку»
Мета:
– вивчення основних положень та визначень з теми «Диференціальні рівняння першого порядку»;
– ознайомлення із видами диференціальних рівнянь першого порядку та методами їх розв'язування;
– розвиток візуального мислення та пам’яті;
– виховання математичної культури.
При вивченні теми студенти повинні:
знати: означення та види диференціальних рівнянь першого порядку;
уміти: визначати диференціальне рівняння першого порядку з переліку рівнянь, знаходити загальний та частинний інтеграл рівняння з відокремлюючими змінними за допомогою теореми Коші;
здатні: використовувати алгоритм розв'язування рівняння з відокремлюючими змінними.
Основні поняття: диференціальне рівняння першого порядку, загальний та частинний інтеграл, особливий розв'язок, рівняння з відокремлюючими змінними.
Обладнання: підручники, дидактичний матеріал (таблиці), креслярські матеріали, мультимедійний проектор, комп’ютер.
Час: 2 год.
План лекції
1. Загальні відомості про диференціальні рівняння першого порядку.
2. Диференціальні рівняння із відокремлюючими змінними.
3. Диференціальні рівняння із змінними, які відокремлюються.
Список літератури
1. Pudy A.E., Rakov S.A. Mathematical Analysis. Differential Equations.
2. Давидов М.О. Курс математичного аналізу: Підручник: У 3 ч. Ч. 2. Функції багатьох змінних і диференціальні рівняння. – 2-ге вид., перероб. і допов. – К.: Вища школа, 1991 – 336 с.
3. Еругин Р.П. и др. Курс обыкновенных дифференциальных уравнений.
4. Матвеев Н.М. Методы интегрирования обыкновенных дифференциальных уравнений.
Текст лекції
1. Загальні відомості про диференціальні рівняння першого порядку.
Означення 1. Диференціальне рівняння першого порядку має вигляд
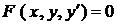 .
.
Якщо це рівняння можна розв'язати відносно  , то його можна записати у вигляді
, то його можна записати у вигляді
 .
.
Для такого рівняння справедлива наступна теорема, яка називається теоремою існування і одиничності розв'язку диференціального рівняння.
Теорема 1. Якщо в рівнянні  функція
функція  і її частинна похідна
і її частинна похідна  по у неперервні в деякій області D на площині 0 ху, яка містить деяку точку
по у неперервні в деякій області D на площині 0 ху, яка містить деяку точку  , то існує єдиний розв'язок цього рівняння
, то існує єдиний розв'язок цього рівняння  ,
,
який задовольняє умові 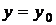 при
при  .
.
Геометричний зміст теореми полягає в тому, що існує і притім єдина функція  , графік якої проходить через точку
, графік якої проходить через точку  .
.
Означення 2. Умова, що при  функція у повинна дорівнюватися заданому числу
функція у повинна дорівнюватися заданому числу  , називається початковою умовою, або умовою Коші. Вона записується у вигляді
, називається початковою умовою, або умовою Коші. Вона записується у вигляді
 або
або 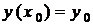 .
.
Означення 3. Задача, у якій потрібно знайти частинний розв'язок рівняння  , який задовольняє початковій умові
, який задовольняє початковій умові 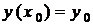 , називається задачею Коші.
, називається задачею Коші.
Означення 4. Загальним розв'язком диференціального рівняння першого порядку називається функція
 ,
,
яка залежить від однієї довільної сталої С і задовольняє наступним умовам:
а) вона задовольняє диференціальному рівнянню при будь-якому конкретному значенні сталої С;
б) яка б не була початкова умова 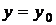 при
при  , тобто
, тобто 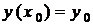 , можна знайти таке значення
, можна знайти таке значення 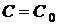 , що функція
, що функція  задовольняє даній початковій умові. При цьому передбачається, що значення
задовольняє даній початковій умові. При цьому передбачається, що значення  і
і  належать до тієї області зміни змінних х і у, у якій виконуються умови теореми існування й одиничності розв'язку.
належать до тієї області зміни змінних х і у, у якій виконуються умови теореми існування й одиничності розв'язку.
У процесі знаходження загального розв'язку диференціального рівняння ми приходимо до співвідношення вигляду
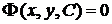 ,
,
не розв'язаному відносно у. Розв'язавши це співвідношення відносно у, одержуємо загальний розв'язок. Однак не завжди удається виразити у в елементарних функціях; у таких випадках загальний розв'язок залишається в неявному вигляді.
Означення 5. Рівність вигляду 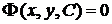 , яка неявно задає загальний розв'язок, називається загальним інтегралом диференціального рівняння.
, яка неявно задає загальний розв'язок, називається загальним інтегралом диференціального рівняння.
Означення 6. Частинним розв'язком називається будь-яка функція  , яка утворюється з загального розв'язку
, яка утворюється з загального розв'язку  , якщо в останньому довільної сталої С придати визначене значення
, якщо в останньому довільної сталої С придати визначене значення 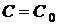 . Співвідношення
. Співвідношення  називається в цьому випадку частинним інтегралом рівняння.
називається в цьому випадку частинним інтегралом рівняння.
З геометричної точки зору загальний інтеграл являє собою сімейство кривих на координатній площині, яке залежить від однієї довільної сталої С. Ці криві називаються інтегральними кривими даного диференціального рівняння. Частинному інтегралу відповідає одна крива цього сімейства, яка проходить через деяку задану точку площини.
Вирішити або проінтегрувати диференціальне рівняння - значить:
а) знайти його загальний розв'язок або загальний інтеграл (якщо початкові умови не задані) або
б) знайти той частинний розв'язок рівняння, який задовольняє заданим початковим умовам (якщо такі є).
Означення 7. Особливим розв'язком називається такий розв'язок, у всіх точках якого умова одиничності не виконується, тобто в будь-якому околі кожної точки  особливого розв'язку існують принаймні дві інтегральні криві, які проходять через цю точку.
особливого розв'язку існують принаймні дві інтегральні криві, які проходять через цю точку.
Особливі розв'язки не утворюються з загального розв'язку диференціального рівняння ні при яких значеннях довільної сталої С (у тому числі і при  ).
).
2. Диференціальні рівняння із відокремлюючими змінними
Означення 8. Диференціальне рівняння типу

називають рівнянням із відокремлюючими змінними, тому що в цьому рівнянні змінні відокремлені, тобто при  знаходиться тільки функція від х, а при
знаходиться тільки функція від х, а при  - тільки функція від у.
- тільки функція від у.
Інтегруючи обидві частини цього рівняння, одержимо співвідношення, яке зв'язує розв'язок у, незалежну змінну х і довільну сталу С, тобто одержимо загальний інтеграл рівняння
 .
.
Приклад. Знайти загальний розв'язок рівняння
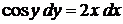 .
.
Розв'язок.  ,
,  ,
,
 .
.
3. Диференціальні рівняння із змінними, які відокремлюються.
Означення 9. Диференціальні рівняння, у яких змінні можна відокремити за допомогою множення або ділення обох частин рівняння на той самий вираз, називаються диференціальними рівняннями із змінними, які відокремлюються.
Це рівняння виду
 .
.
Воно може бути приведене до рівняння із відокремленими змінними шляхом ділення обох його частин на вираз  :
:
 , або
, або
 .
.
Приклад. Знайти загальний розв'язок рівняння
 .
.
Розв'язок. Відокремлюючи змінні, знаходимо:
 ,
, 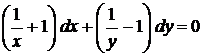 .
.
Інтегруючи, отримаємо: 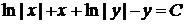 або
або  .
.
Останнє співвідношення є загальний інтеграл даного рівняння.
Приклад. Розв'язати задачу Коші
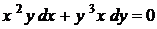 ,
,  .
.
Розв'язок. Відокремлюючи змінні, знаходимо:
 .
.
Інтегруючи, отримаємо:  ,
,
 .
.
Одержали загальний інтеграл вихідного рівняння.
Розв'язавши останнє рівняння відносно у, знайдемо загальний розв'язок вихідного рівняння
 ,
, 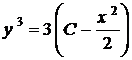 ,
,  .
.
Знайдемо частинний розв'язок, який задовольняє початковій умові  .
.
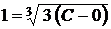 ,
,  ,
,  ,
,  .
.
 - розв'язок задачі Коші.
- розв'язок задачі Коші.
Лекція 3
 2017-12-14
2017-12-14 634
634








