Тема: «Лінійні диференціальні рівняння першого порядку»

Мета:

– вивчення основних положень та визначень з теми «Лінійні диференціальні рівняння першого порядку»;

– ознайомлення із видами лінійних рівнянь першого порядку та методами їх розв'язування;

– поглиблення, розширення знань, отриманих раніше при вивченні диференціальних рівнянь, для розв'язування лінійних рівнянь;

– розвиток візуального мислення та пам’яті;

– виховання математичної культури.

При вивченні теми студенти повинні:

знати: означення та види лінійних рівнянь першого порядку, методи їх розв'язування;

уміти: визначати лінійне рівняння першого порядку з переліку рівнянь, знаходити загальний та частинний розв'язок лінійного рівняння як однорідного, так і неоднорідного;

здатні: використовувати алгоритм розв'язування лінійних рівнянь першого порядку.

Основні поняття: лінійне рівняння першого порядку (лінійне однорідне, лінійне неоднорідне), підстановка та рівняння Бернуллі, метод Лагранжа.

Обладнання: підручники, дидактичний матеріал (таблиці), креслярські матеріали, мультимедійний проектор, комп’ютер.

Час: 2 год.

План лекції

1. Загальні відомості про лінійні рівняння першого порядку.

2. Рівняння Бернуллі.

3. Метод Лагранжа (метод варіації довільної змінної) для розв'язку лінійних рівнянь першого порядку.

Список літератури

1. Pudy A.E., Rakov S.A. Mathematical Analysis. Differential Equations.

2. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного.

3. Давидов М.О. Курс математичного аналізу: Підручник: У 3 ч. Ч. 2. Функції багатьох змінних і диференціальні рівняння. – 2-ге вид., перероб. і допов. – К.: Вища школа, 1991 – 336 с.

4. Матвеев Н.М. Методы интегрирования обыкновенных дифференциальных уравнений.

Текст лекції

1. Загальні відомості про лінійні рівняння першого порядку.

Означення 1. Лінійним рівнянням першого порядку називається рівняння, що має вигляд

, (1)

де і - задані неперервні функції від х (або сталі).

Якщо , то рівняння називається лінійним однорідним.

Якщо , то рівняння називається лінійним неоднорідним.

Шукаємо розв'язок рівняння (1) у вигляді добутку двох функцій від х:

, (2)

. (3)

Підставивши у і в (1), маємо:

,

. (4)

Виберемо функцію такою, щоб

, (5)

, , ,

, ,

, .

Так як нам досить якого-небудь відмінного від нуля розв'язку рівняння (5), то за функцію візьмемо .

Підставляючи знайдене значення в (4), одержимо:

, , , .

Підставляючи й у (2), одержуємо розв'язок неоднорідного рівняння:

,

. (6)

Розв'язок однорідного рівняння можна записати у вигляді:

, , ,

, .

Приклад. Розв'язати рівняння

.

Розв'язок. Скориставшись (2), (3) , , маємо:

, .

Згідно методу виберемо функцію такою, щоб , тоді

, ,

.

, , , ,

.

Підставляючи й , одержуємо загальний розв'язок рівняння:

.

Рівняння Бернуллі

Означення 2. РівняннямБернуллі називається рівняня виду 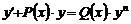або .

Рівняння Бернуллі відрізняється від лінійного правою частиною і зводиться до послідовності рівнянь з відокремлюючими змінними за тією ж схемою, що і лінійне, з підстановкою

або

Приклад 1. Знайти загальний розв'язок диференціального рівняння .

1⁰. Визначаємо тип диференціального рівняння (таблиця 1):

- рівняння Бернуллі, де .

2⁰. Запишемо підстановку:

.

3⁰. Здійснимо підстановку в дане рівняння:

4⁰. Запишемо послідовність рівнянь відносно функцій та . Згрупуємо перший і третій члени рівняння:

Виберемо функцію так, щоб вона перетворювалася в нуль дужку, отримаємо послідовність функцій:

5⁰. Знайдемо функції та . Кожне з рівнянь послідовності є рівнянням з відокремлюючими змінними:

6⁰. Запишемо загальний розв'язок диференціального рівняння:

3. Метод Лагранжа (метод варіації довільної змінної) для розв'язку лінійних рівнянь першого порядку

Суть методу полягає в тому, що спочатку знаходимо загальний розв'язок відповідного лінійного однорідного рівняння

.
Потім, вважаючи в цьому розв'язку сталу С функцією від х, шукаємо розв'язок лінійного неоднорідного рівняння у вигляді:

. (7)
Розв'язок (7) повинен задовольняти рівняння (1). Диференціюючи і підставляючи (7) в (1), маємо:

,

,

, ,

,

. (8)

Він співпадає з розв'язком (6).

Приклад. Розв'язати рівняння методом Лагранжа

.

Розв'язок. Розв'яжемо відповідне однорідне рівняння

, ,

, .

Вважаючи в цьому розв'язку сталу С функцією від х, шукаємо розв'язок лінійного неоднорідного рівняння у вигляді:

, .

Підставимо у вихідне рівняння у, і з отриманого диференціального рівняння знайдемо функцію :

,

, .

- загальний розв'язок.

Тому що , то - теж розв'язок вихідного рівняння.

Лекція 5