Мета:
– вивчення основних положень та визначень з теми «Диференціальні рівняння в повних диференціалах»;
– ознайомлення із видами рівнянь в повних диференціалах та методами їх розв'язування;
– поглиблення, розширення знань, отриманих раніше при вивченні диференціальних рівнянь, для розв'язування рівнянь в повних диференціалах;
– розвиток наукового мислення та пам’яті;
– виховання математичної культури.
При вивченні теми студенти повинні:
знати: означення інтегруючого множника, означення та види рівнянь в повних диференціалах, методи їх розв'язування;
уміти: визначати рівняння в повних диференціалах з переліку рівнянь, знаходити інтегруючий множник для рівняння, яке зводиться до рівняння в повних диференціалах;
здатні: використовувати алгоритм розв'язування рівнянь в повних диференціалах.
Основні поняття: рівняння в повних диференціалах, інтегруючий множник.
Обладнання: підручники, дидактичний матеріал (таблиці), креслярські матеріали, мультимедійний проектор, комп’ютер.
Час: 2 год.
План лекції
1. Загальні відомості про рівняння в повних диференціалах.
2. Інтегруючий множник
Список літератури
1. Pudy A.E., Rakov S.A. Mathematical Analysis. Differential Equations.
2. Арнольд В.И. Обыкновенные дифференциальные уравнения.
3. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного.
4. Давидов М.О. Курс математичного аналізу: Підручник: У 3 ч. Ч. 2. Функції багатьох змінних і диференціальні рівняння. – 2-ге вид., перероб. і допов. – К.: Вища школа, 1991 – 336 с.
5. Еругин Р.П. и др. Курс обыкновенных дифференциальных уравнений.
6. Матвеев Н.М. Методы интегрирования обыкновенных дифференциальных уравнений.
Текст лекції
1. Загальні відомості про рівняння в повних диференціалах.
Означення 1. Рівняння  називається рівнянням в повних диференціалах, якщо його ліва частина – повний диференціал деякої функції
називається рівнянням в повних диференціалах, якщо його ліва частина – повний диференціал деякої функції  , тобто
, тобто
 .
.
Необхідною і достатньою умовою повного диференціала є рівність частинних похідних  .
.
Загальний інтеграл рівняння в повних диференціалах має вигляд  ,
,
Де функція  може бути знайдена за однією із формул:
може бути знайдена за однією із формул:

Приклад 1. Вказати рівняння в повних диференціалах:
а) 
10. Диференціальне рівняння записано в симетричній формі, де
 ,
, 
20. Знайдемо частинні похідні:
 ,
,  .
.
30. Порівняємо частинні похідні. Так як  , то рівняння є рівнянням в повних диференціалах.
, то рівняння є рівнянням в повних диференціалах.
б) 
10. Диференціальне рівняння записано в симетричній формі, де
 ,
, 
20. Знайдемо частинні похідні:
 ,
,  .
.
30. Порівняємо частинні похідні. Так як  , то рівняння є рівнянням в повних диференціалах.
, то рівняння є рівнянням в повних диференціалах.
Приклад 2. Знайти загальний інтеграл диференціального рівняння
 .
.
10. Визначаємо тип рівняння (таблиця 1):
Запишемо рівняння в симетричній формі
 ,
,  ,
,  ,
,
тоді
 ,
, 
1.2. Знайдемо частинні похідні:
 ,
,
 .
.
1.3. Порівняємо частинні похідні. Так як  , то рівняння є рівнянням в повних диференціалах.
, то рівняння є рівнянням в повних диференціалах.
20. Запишемо формулу загального інтеграла:

30. Виберемо формулу для відшукання функції  :
:

40. Знайдемо функцію  :
:

50. Запишемо загальний інтеграл рівняння:

Приклад 3. Знайти загальний інтеграл диференціального рівняння 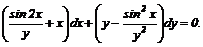
Відповідь: 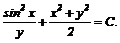
Приклад 4. Серед рівнянь вказати те, яке є одночасно однорідним і в повних диференціалах:
а) 
б) 
в) 
2. Інтегруючий множник
Нехай функції  неперервні в області
неперервні в області  вигляду
вигляду  . Якщо для рівняння
. Якщо для рівняння
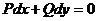 (1)
(1)
умова 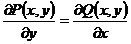 не виконується в області
не виконується в області  , то це рівняння не буде рівнянням у повних диференціалах у цій області.
, то це рівняння не буде рівнянням у повних диференціалах у цій області.
В цьому разі виникає питання, чи не можна підібрати функцію  так, щоб після множення на неї рівняння (1) дістали рівняння
так, щоб після множення на неї рівняння (1) дістали рівняння
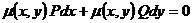 (1’)
(1’)
в повних диференціалах. Така функція називається інтегруючим множником диференціального рівняння (1).
Щоб функція  , неперервна в однов’язній області
, неперервна в однов’язній області  разом зі своїми частинними похідними
разом зі своїми частинними похідними  і
і  , була інтегруючим множником рівняння (1), необхідно і достатньо, щоб для всіх точок
, була інтегруючим множником рівняння (1), необхідно і достатньо, щоб для всіх точок  виконувалась рівність
виконувалась рівність
 ,
,
тобто
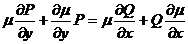 . (2)
. (2)
Рівність (2) містить невідому функцію  під знаком частинних похідних, тобто (2) є диференціальне рівняння в частинних похідних. Його розв’язання є задачею складнішою, ніж розв’язання рівняння (1). Однак задача по знаходженню інтегруючого множника значно спрощується, коли відомо, що він залежить від однієї незамкненої змінної
під знаком частинних похідних, тобто (2) є диференціальне рівняння в частинних похідних. Його розв’язання є задачею складнішою, ніж розв’язання рівняння (1). Однак задача по знаходженню інтегруючого множника значно спрощується, коли відомо, що він залежить від однієї незамкненої змінної  або
або 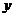 .
.
Припустимо, що рівняння (1) має інтегруючий множник, залежний тільки від  . В цьому разі рівняння (2) набере вигляду
. В цьому разі рівняння (2) набере вигляду
 ,
,
або 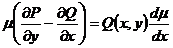 ,
,
звідки  . (3)
. (3)
Оскільки  є функцією однієї незалежної змінної
є функцією однієї незалежної змінної  , то вираз
, то вираз
 (4)
(4)
не повинен залежати від 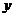 . Позначивши його через
. Позначивши його через  і припускаючи, що
і припускаючи, що  - неперервна функція в інтервалі
- неперервна функція в інтервалі  , з (3) дістанемо
, з (3) дістанемо
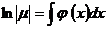
і, таким чином,
 , де
, де  . (5)
. (5)
Покажемо, що коли вираз (4) справді не залежить від 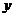 і є неперервною функцією від
і є неперервною функцією від  на інтервалі
на інтервалі  , то функція
, то функція  , задана рівністю (5), є інтегруючим множником рівняння (1).
, задана рівністю (5), є інтегруючим множником рівняння (1).
Справді, для цього достатньо переконатись у справедливості рівності
 (6)
(6)
для всіх точок  . Маємо
. Маємо
 ,
,
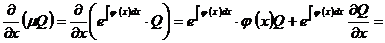
 ,
,
тобто рівність (6) дійсно виконується в області  .
.
В аналогічній спосіб можна показати, що коли вираз

не залежить від  і є неперервною в інтервалі
і є неперервною в інтервалі  , то рівняння (1) має інтегруючий множник, незалежний від
, то рівняння (1) має інтегруючий множник, незалежний від  , який знаходиться за формулою
, який знаходиться за формулою
 .
.
Розглянемо питання про еквівалентність рівнянь (1) і (1’). Якщо  є інтегруючий множник рівняння (1), то рівняння
є інтегруючий множник рівняння (1), то рівняння
 (7)
(7)
є рівнянням в повних диференціалах, тобто існує функція  , повний диференціал якої дорівнює лівій частині цього рівняння:
, повний диференціал якої дорівнює лівій частині цього рівняння:
 . (8)
. (8)
Загальний інтеграл рівняння (7) має вигляд
 .
.
З (8) дістанемо
 (9)
(9)
і, отже, ліва частина (9) може перетворитись у нуль не тільки при  , але й при
, але й при  . (10)
. (10)
Якщо рівняння (10) задає 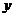 як деяку функцію від
як деяку функцію від  або
або  як деяку функцію від
як деяку функцію від 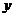 , то вона є розв’язком рівняння
, то вона є розв’язком рівняння
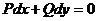 (11)
(11)
що не міститься в загальному інтегралі  рівняння (7).
рівняння (7).
Крім того, якщо рівняння
 (12)
(12)
задає деяку функцію 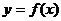 або
або  , то з (7), видно, що ця функція ввійде в загальний інтеграл рівняння (5), однак може виявитись побічним розв’язком рівняння (11).
, то з (7), видно, що ця функція ввійде в загальний інтеграл рівняння (5), однак може виявитись побічним розв’язком рівняння (11).
Таким чином, щоб дістати загальний інтеграл рівняння (11), треба взяти загальний інтеграл рівняння (7) і з нього вилучити ті розв'язки рівняння (12), які не є розв'язками рівняння (11), і додати ті розв'язки рівняння (10), які не є розв'язками рівняння (7).
Приклад 1. Розв’язати рівняння
 (13)
(13)
Розв’язання. Тут 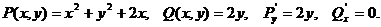 Функції
Функції 
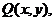
 і
і  неперервні в усій площині
неперервні в усій площині  , однак умова
, однак умова  не виконана і, отже, рівняння (13) не є рівнянням у повних диференціалах. Вираз (4)
не виконана і, отже, рівняння (13) не є рівнянням у повних диференціалах. Вираз (4)  не залежить від
не залежить від 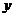 і являє собою неперервну функцію від
і являє собою неперервну функцію від 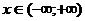 . Тому інтегруючий множник визначається за формулою (5)
. Тому інтегруючий множник визначається за формулою (5)
 .
.
Помноживши на цей множник праву і ліву частини рівняння (13), дістанемо рівняння в повних диференціалах 
Функцію  , повний диференціал якої дорівнює лівій частині останнього рівняння, знаходимо з рівнянь
, повний диференціал якої дорівнює лівій частині останнього рівняння, знаходимо з рівнянь



З першого рівняння маємо

Звідси і з другого рівняння знаходимо



Таким чином, загальний інтеграл рівняння (13) має вигляд

Опорні конспекти лекцій змістовного модуля I
Лекція 1. Диференціальні рівняння, основні визначення.













|

|

|
|

|
|

Лекція 2. Диференціальні рівняння першого порядку.







|



|



|
|

 |
Лекція 3. Однорідні рівняння першого порядку.


|

|
|

Лекція 4. Лінійні диференціальні рівняння першого порядку.


 |  | |||||||||||
 |  | |||||||||||
 |  | |||||||||||
 |
Лекція 5. Диференціальні рівняння в повних диференціалах.
|

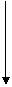



 | |||
 |
 Розробка практичних занять для змістовного модуля І
Розробка практичних занять для змістовного модуля І
Практичне заняття 1
 2017-12-14
2017-12-14 1520
1520

 , яка задовольняє диференціальне рівняння в області визначення всіх незалежних змінних
, яка задовольняє диференціальне рівняння в області визначення всіх незалежних змінних  .
.  особливого розв'язку існують принаймні дві інтегральні криві, які проходять через цю точку.
особливого розв'язку існують принаймні дві інтегральні криві, які проходять через цю точку.  ;
;  ;
;  .
.  ;
;  ;
; 
 є
є 






