Окружности, расположенные в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрическую плоскость проекций в виде эллипсов (рис. 7). Если диметрическую проекцию выполняют без искажения по осям x` и z`, то большая ось эллипсов 1, 2, 3 равна 1,06 диаметра окружности, а малая ось эллипса 1 – 0,95 и эллипсов 2 и 3 – 0,35 диаметра окружности. Если диметрическую проекцию выполняют с искажением по осям x` и z`, то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а малая ось эллипса 1 – 0,9 и эллипсов 2 и 3 – 0,33 диаметра окружности. Малые оси эллипсов, как и в изометрической проекции, располагают параллельно отсутствующей в плоскости эллипса аксонометрической оси, а большие оси эллипсов – перпендикулярно малым осям. Так, на рис. 7 малая ось K`L` эллипса 1 расположена параллельно оси y`, а большая ось E`F` – под углом 90o к оси y`; малая ось C`D` эллипса 2 расположена параллельно оси z`, а большая ось А`В` – под углом 90o к оси z`. На практике эллипсы, так же как и в изометрической проекции, разрешается заменять четырехцентровыми овалами. Способы построения овалов в диметрической проекции показаны на рис. 8.

Рис. 7
Для построения диметрической проекции окружности, расположенной параллельно плоскости П2, откладывают на осях x` и z` от точки пересечения аксонометрических осей радиус R данной окружности (рис. 8, а). Из полученной точки 1` проводят горизонтальную линию до пересечения с большой и малой осями эллипса в точках О1 и О2. Зная положение точек О1 и О2, легко найти симметричные им точки О3 и О4. Точки О3 и О4 можно также определить проведением горизонтальной линии из точки 3`. Приняв за центры точки О1 и О3, радиусом R1 проводят дуги 1` 2` и 3` 4`. Приняв за центры точки О2 и О4, проводят радиусом R2 замыкающие овал дуги 1` 4` и 2` 3`.
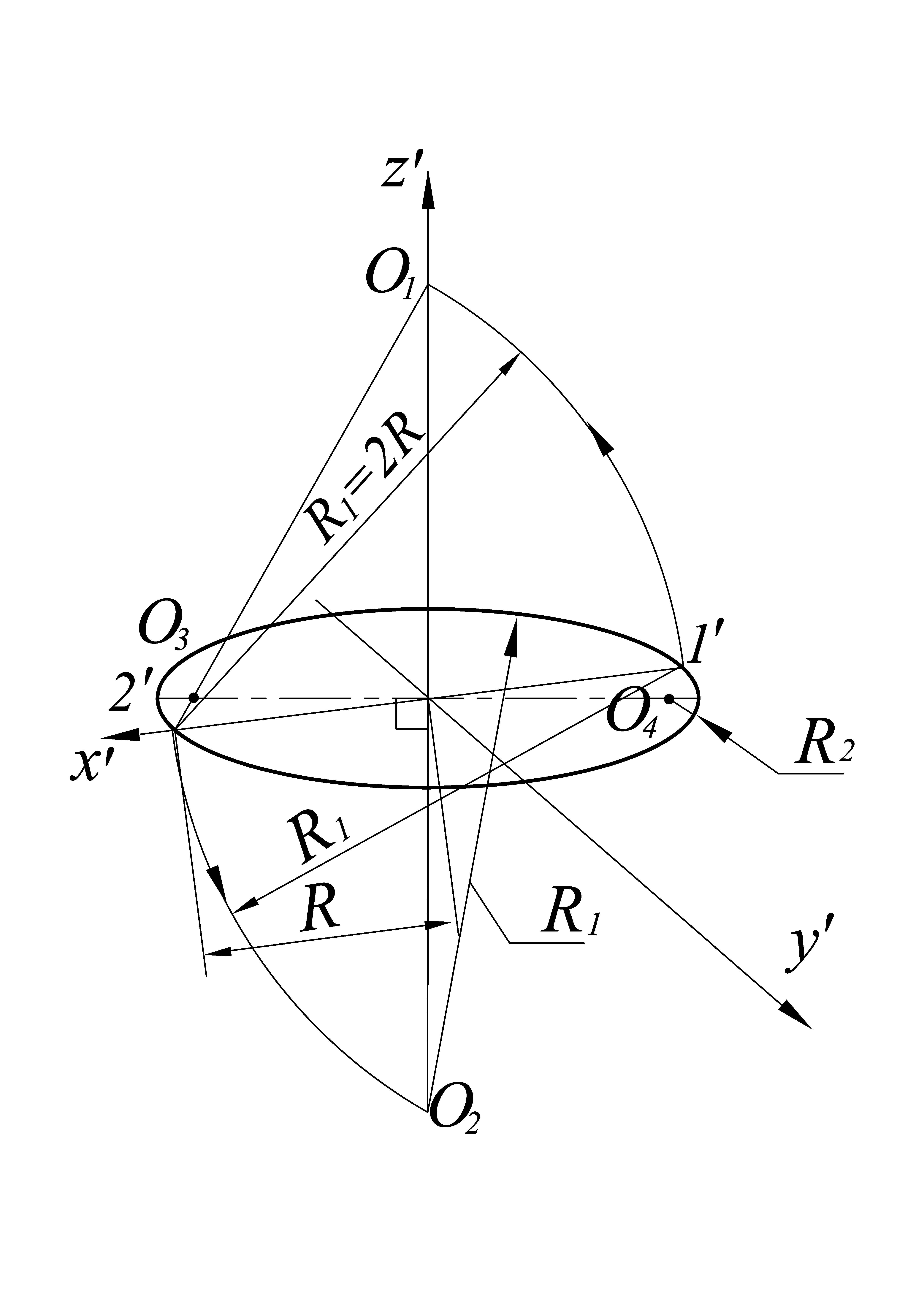
Рассмотрим упрощенное построение диметрической проекции окружности, лежащей в плоскости П1 (рис. 8, б). Через заданную точку О` проводят аксонометрические оси x`, y` и z`. На оси x` от точки О` откладывают радиус заданной окружности, т.е. О`1`= O`2` = R, а на оси y` – отрезки, равные R/2. Из полученных точек 1` и 2` радиусом R1 = 2R описывают дуги окружностей до пересечения с осью z` в точках О1, О2 – центрах дуг овала. Точки О3, О4 – центры замыкающих дуг овала получают на пересечении прямых О12` и О21` с горизонтальной прямой, проходящей через центр О`. Из центров О1 и О2 описывают дуги радиусом R1, а из центров О3 и О4 – дуги радиусом R2 = О32` = О41`. Аналогично строится диметрическая проекция окружности, расположенной в плоскости П3.
 |  |
| а) | б) |
Рис. 8
 2017-12-14
2017-12-14 3491
3491
