Таблица основных интегралов
1. 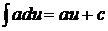 (
(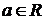 ,
, 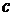 – const,
– const, 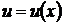 )
)
2. 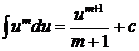 (для любого
(для любого 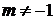 )
)
2.1. 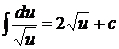 2.2.
2.2. 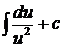
3. 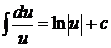
4. 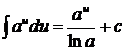 (
(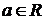 ,
, 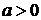 ,
, 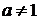 )
)
5. 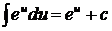
6. 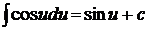
7. 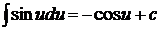
8. 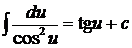
9. 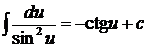 10.
10. 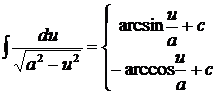 (
(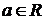 )
)
11. 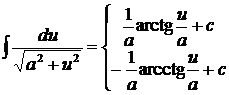 (
(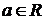 )
)
12. 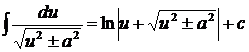
13. 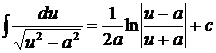
При интегрировании используются свойства интегралов.
Свойства интегралов
1) 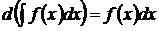
2) 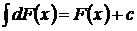 , в частности,
, в частности, 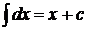
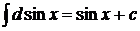 ,
, 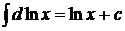
3) 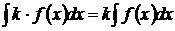 , где
, где 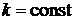
4) 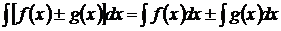
Таблицу интегралов и свойства необходимо выучить наизусть.
МЕТОДЫ ИНТЕГРИРОВАНИЯ
Существуют три способа интегрирования: непосредственное, заменой переменной и по частям.
Непосредственное интегрирование
Непосредственное интегрированиесостоит в том, что подынтегральную функцию путем тождественных преобразований с использованием формул алгебры и тригонометрии, а также, используя свойства (3) и (4), сводят к табличным интегралам.
Рассмотрим несколько примеров.
Пример. 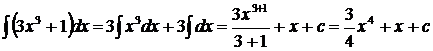 .
.
(Использованы свойства 3, 4; табличный интеграл 2, 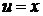 ).
).
Правильность ответа проверяем дифференцированием:
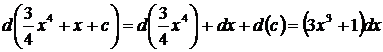 .
.
Пример. 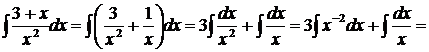
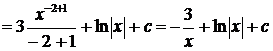 .
.
(Свойства 3, 4; табличные интегралы 2.2 и 3).
Пример. 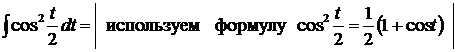
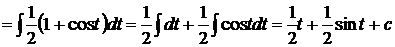 .
.
(Свойства 3,4; табличные интегралы 1 и 7).
Метод замены переменной (подстановки)
Для вычисления интеграла 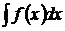 сделаем замену
сделаем замену 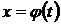 , где
, где 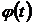 выбирается так, чтобы после преобразований данного интеграла и новой переменной
выбирается так, чтобы после преобразований данного интеграла и новой переменной 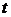 , получился интеграл, который берется непосредственно.
, получился интеграл, который берется непосредственно.
Предварительно находим 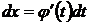 , тогда
, тогда
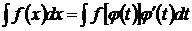 . (4)
. (4)
После нахождения первообразной 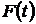 необходимо вернуться к первоначальной переменной «
необходимо вернуться к первоначальной переменной « ».
».
Пример. 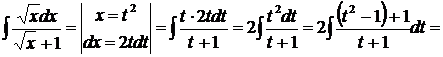
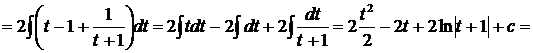
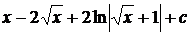 .
.
Пример 18. 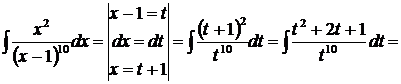
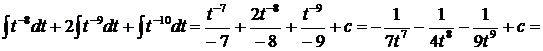
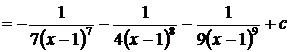 .
.
Замечание. Следующие интегралы удобно решать указанной заменой:
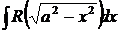 ,
, 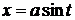 ;
; 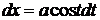 ;
;
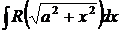 ,
, 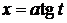 ;
; 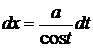 ;
;
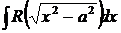 ,
, 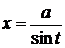 ;
; 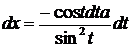 .
.
Пример. 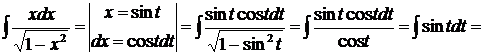
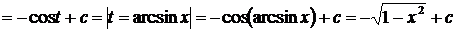 ,
,
т. к. 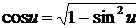 .
.
Формулой (4) часто пользуются справа налево:
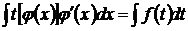 ,
, 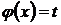 . (5)
. (5)
При этой замене надо помнить, что в составе подынтегрального выражения должен быть дифференциал функции 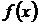 .
.
Такой метод называется подведением под знак дифференциала
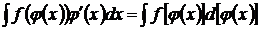 . (5’)
. (5’)
При использовании этого метода можно воспользоваться таблицей дифференциалов.
Таблица дифференциалов
1. 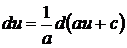 ,
, 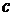 – const,
– const, 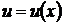 ,
, 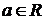
2. 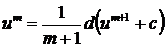
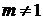
3. 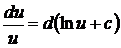
4. 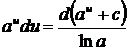 ,
, 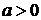 ,
, 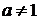 ,
, 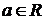
5. 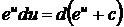
6. 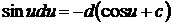
7. 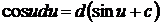
8. 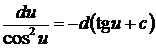
9. 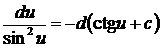
10. 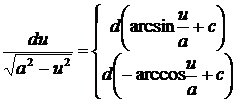 ,
, 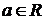
11. 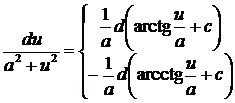 ,
, 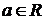
Пример. 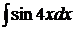 .
.
Решение. Согласно таблице дифференциалов, 1, с. 7 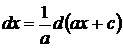 , положим
, положим 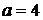 ,
, 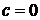 ,
, 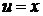 ,
, 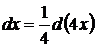 .
.

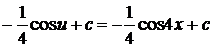 .
.
Пример. 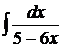 .
.
Решение. По таблице дифференциалов, 1, с. 7 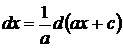 , положим
, положим
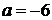 ,
, 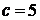 ,
, 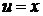 ,
, 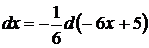 .
.
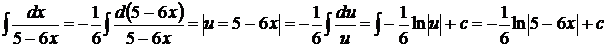 .
.
Пример. 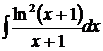 – можно найти двумя способами:
– можно найти двумя способами:
1 способ. 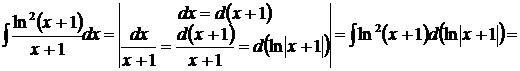
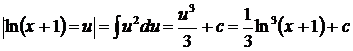 ;
;
2 способ. 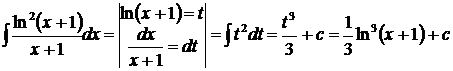 .
.
Пример. 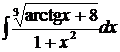 .
.
1 способ. 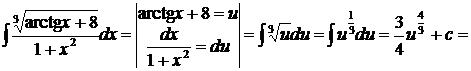
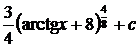 ;
;
2 способ. 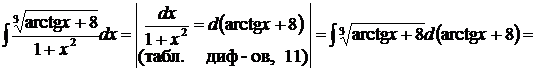
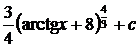 .
.
Пример. 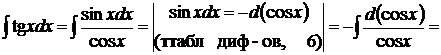
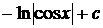 . (табл. интегр., 3,
. (табл. интегр., 3, 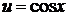 ).
).
 2017-12-14
2017-12-14 326
326







