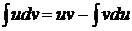Метод интегрирования по частям. Эта формула чаще всего применяется тогда, когда под интегралом имеется произведение алгебраической и трансцендентной функции

(6)

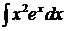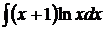Эта формула чаще всего применяется тогда, когда под интегралом имеется произведение алгебраической и трансцендентной функции, например, или , или .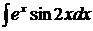

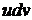– это все подынтегральное выражение, часть которого мы обозначаем за 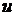, а часть за 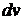. При этом:

1) за 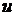принимается функция, которая дифференцированием упрощается.

2) за 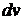– та часть, интеграл от которой известен или легко может быть взят.

3) в состав 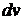обязательно входит .

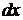В итоге верного выбора 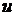и и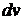нтеграл в (20) должен быть проще исходного.

Пример.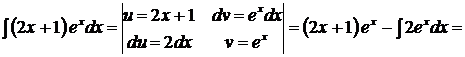

.

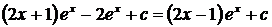Замечание. Метод интегрирования по частям может применяться в одном примере несколько раз.

Замечание. Иногда повторное интегрирование по частям приводит к уравнению искомого интеграла 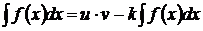, , 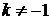если

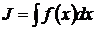, то получаем уравнение: 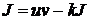, откуда

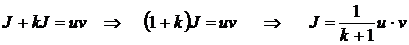или .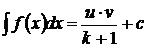

Пример. 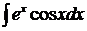– решить методом по частям, используя примечание. При верном решении должен получиться ответ:

.

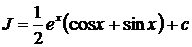Только по частям берутся интегралы:

а) 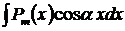, 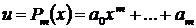многочлен 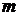-ой степени,

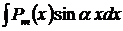, в частности одночлен

, ,

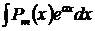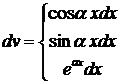б) , ,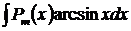

,

, ,

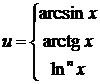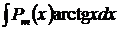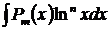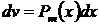в) , , ,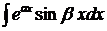

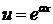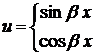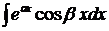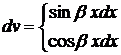, или .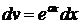

Интегралы типа (в) интегрируются дважды по частям.

Пример.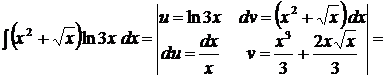

.

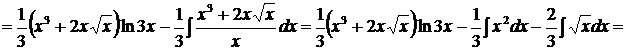
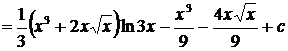Рассмотрим отдельные классы функций и способы их интегрирования.

 

ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ