Простейшие дроби, их интегрирование

К простейшим дробям относятся дроби вида:

1. , 2. , 3. , при ,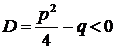

4. , при (, , , , , ).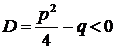

При интегрировании дробей типа 1 – 2 достаточно ввести подстановку , (или ), тогда

1. ;

2. , ().

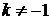Чтобы проинтегрировать дроби типа 3 – 4, необходимо выделить полный квадрат из квадратного трехчлена, затем свести интеграл к табличному.

Пример. .

Решение. Выделим полный квадрат из квадратного трехчлена:

.

=

(табл. интегр., 11).

Замечание. При интегрировании дробей типа 3 – 4 можно воспользоваться справочником.

 

Правильные и неправильные рациональные дроби

Определение Дробь называется рациональной, где , 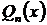– многочлены 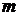-ой и -ой степеней.

Если , дробь неправильная.

Если 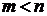, дробь правильная.

Неправильную дробь представляют в виде суммы целой части и правильной дроби. Операция выделения целой части может быть выполнена делением числителя на знаменатель.

Пример. Дробь неправильная (, , ). Выделим целую часть, разделив числитель на знаменатель.

 

.

Пример. Дробь правильная, т. к. , , .

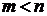Пример1. Дробь неправильная (, , ).

.