Из чертежа видно, что

4 x пределы интегрирования

будут и

(рис. 3).

Рис. 3 .

(кв. ед.).

 

Пример. Вычислить длину одной арки циклоиды

(рис. 4).

Решение. Из соотношения видно, что значение соответствует ,

соответствует ,

. Так как уравнение линии

задано в декартовых координатах,

то используем формулу

: , .

t=0 t= t=2

 

Рис. 4

.

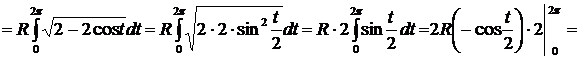
Пример. Вычислить длину кардиоиды ,

соответствующую .

Решение. Уравнение кривой задано в полярных координатах, следовательно, при решении воспользуемся формулой . Изменение задано, следовательно, выполнение чертежа необязательно.

(ед. длины).

Пример. Вычислить объем тела, образованного вращением вокруг оси фигуры, ограниченной параболой и осью (рис. 5).

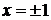Решение. Парабола расположена ветвями вниз, вершина находится в точке , и ось пересекает в точках . Для решения воспользуемся формулой

(куб. ед.).

y

 

1

 

1 x

 

Рис. 5

Пример. Вычислить объем тела, образованного вращением гиперболы , отсеченной прямыми , вокруг оси (рис. 6).

Решение. Для решения задачи воспользуемся формулой

y

; ,

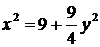находим из уравнения гиперболы:

-3 3 x

Рис. 6 (куб. ед.).

Замечание: Иногда при решении задач полезно использовать рекуррентную формулу:

Знак (двойной факториал) означает произведение целых чисел, начиная с , через одно с убыванием. Например, (только нечетные множители).