1. Правило фаз Гиббса и дисперсность. Влияние кривизны поверхности (дисперсности) на внутреннее давление тел (вывод и анализ уравнения Лапласа). Капиллярные явления (уравнение Жюрена).
Дисперсность является самостоятельным и полноправным термодинамическим параметром системы, а для дисперсных систем правило фаз Гиббса принимает следующий вид:

F – количество степеней свободы, К – количество компонентов, Ф – количество фаз.
 Рассмотрим результат влияния кривизны поверхности раздела между двумя несмешивающимися жидкостями на внутреннее давление в фазах.
Рассмотрим результат влияния кривизны поверхности раздела между двумя несмешивающимися жидкостями на внутреннее давление в фазах.
Кривизна вызывает изменение площади и положения межфазной поверхности, что можно выразить приращением поверхностной энергии σds. Кроме того, изменяются объемы фаз V1 и V2 на dV1 и dV2. При условии постоянства объема всей системы dV1 = - dV2. Изменение объемов вызывает соответствующие изменения энергий фаз 1 и 2 на p1dV1 и p2dV2 (где p1 и р2 — давления внутри фаз). Соотношение между поверхностной энергией и «объемной» можно записать с помощью обобщенного уравнения первого и второго начал термодинамики относительно энергии Гельмгольца F при T=const: 
При равновесии между фазами ΔF = 0, тогда 
Это уравнение называется уравнением Лапласа.
Для сферической поверхности  и уравнение принимает вид
и уравнение принимает вид 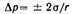 .
.
Капиллярные явления наблюдаются в содержащих жидкость узких сосудах (капилляры, капиллярно-пористые тела), у которых расстояние между стенками соизмеримо с радиусом кривизны поверхности жидкости. Кривизна возникает в результате взаимодействия жидкости со стенками сосуда (адгезия, смачивание). Специфика поведения жидкости в капиллярных сосудах зависит от того, смачивает или не смачивает жидкость стенки сосуда, точнее, от значения краевого угла.
 Рассмотрим положение уровней жидкости в двух капиллярах, один из которых имеет лиофильную поверхность и поэтому стенки его смачиваются, у другого внутренняя поверхность лиофобизирована и не смачивается. В первом капилляре поверхность жидкости имеет отрицательную кривизну, поэтому дополнительное давление Лапласа стремится растянуть жидкость (давление направлено к центру кривизны) и поднимает ее в капилляре. Кривизна поверхности жидкости во втором капилляре положительна, дополнительное давление направлено внутрь жидкости, в результате жидкость в капилляре опускается (отрицательное капиллярное поднятие). При равновесии лапласовское давление равно гидростатическому давлению столба жидкости высотой h:
Рассмотрим положение уровней жидкости в двух капиллярах, один из которых имеет лиофильную поверхность и поэтому стенки его смачиваются, у другого внутренняя поверхность лиофобизирована и не смачивается. В первом капилляре поверхность жидкости имеет отрицательную кривизну, поэтому дополнительное давление Лапласа стремится растянуть жидкость (давление направлено к центру кривизны) и поднимает ее в капилляре. Кривизна поверхности жидкости во втором капилляре положительна, дополнительное давление направлено внутрь жидкости, в результате жидкость в капилляре опускается (отрицательное капиллярное поднятие). При равновесии лапласовское давление равно гидростатическому давлению столба жидкости высотой h:


Чтобы высоту капиллярного поднятия связать с характеристикой смачивания, радиус мениска необходимо выразить через угол смачивания θ и радиус капилляра r0. На рисунке показан мениск жидкости в капилляре. Видно, что r0 = r·соsθ, тогда высоту капиллярного поднятия можно представить в виде формулы Жюрена:

 Нередко приходится наблюдать, как жидкость не может вытечь из капилляра под действием силы тяжести. Это объясняется проявлением действия капиллярного потенциала, направленного против силы тяжести, так как на нижнем конце капилляра жидкость образует мениск с положительной кривизной. Если часть капилляра, находящаяся над жидкостью, меньше высоты поднятия жидкости, жидкость из него не вытекает, так как кривизна мениска жидкости вверху капилляра становится положительной (положительный радиус кривизны), отвечающей гидростатическому давлению столба жидкости, равному размеру (высоте) капилляра, т. е. устанавливается равновесие.
Нередко приходится наблюдать, как жидкость не может вытечь из капилляра под действием силы тяжести. Это объясняется проявлением действия капиллярного потенциала, направленного против силы тяжести, так как на нижнем конце капилляра жидкость образует мениск с положительной кривизной. Если часть капилляра, находящаяся над жидкостью, меньше высоты поднятия жидкости, жидкость из него не вытекает, так как кривизна мениска жидкости вверху капилляра становится положительной (положительный радиус кривизны), отвечающей гидростатическому давлению столба жидкости, равному размеру (высоте) капилляра, т. е. устанавливается равновесие.
2. Природа броуновского движения. Понятие и определение среднеквадратичного сдвига по выбранному направлению. Взаимосвязь между среднеквадратичным сдвигом и коэффициентом диффузии (ввод уравнения Эйнштейна-Смолуховского). Следствия из теории броуновского движения.
Основой доказательства теплового молекулярного движения в телах явилось обнаруженное английским ботаником Робертом Броуном в 1827 г. с помощью микроскопа непрерывное движете очень мелких частичек — спор папоротника (цветочной пыльцы), взвешенных в воде. Более крупные частицы находились в состоянии постоянного колебания около положения равновесия. Колебания и перемещения частиц ускорялись с уменьшением их размера и повышением температуры и не были связаны с какими-либо внешними механическими воздействиями.
Теоретически обоснованная интерпретация броуновского движения — участие частиц дисперсной фазы ультрамикрогетерогенных систем в тепловом движении — была дана независимо друг от друга Эйнштейнии (1905 г.) и Смолуховским (1906 г.).
 Проведенными исследованиями была окончательно доказана природа броуновского движения. Молекулы среды (жидкости или газа) сталкиваются с частицей дисперсной фазы, в результате чего она получает огромное число ударов со всех сторон.
Проведенными исследованиями была окончательно доказана природа броуновского движения. Молекулы среды (жидкости или газа) сталкиваются с частицей дисперсной фазы, в результате чего она получает огромное число ударов со всех сторон.
Эйнштейн и Смолуховский для количественного выражения броуновского движения частиц ввели представление о среднем сдвиге частицы. Если при наблюдении движения частицы золя под микроскопом через определенные равные промежутки времени отмечать ее местонахождение, то можно получить ее траекторию движения. Так как движение происходит в трехмерном пространстве, то квадрат среднего расстояния, проходимого частицей за любой промежуток времени, равен  .
.
Под микроскопам наблюдают проекцию смещения частицы на плоскость за какое-то время, поэтому 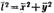 .
.
При равновероятных отклонениях частицы ее направление будет находиться между направлениями x и у, т. е. под углом 45° к каждой координате. Отсюда  или
или 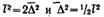 .
.
Из-за равновероятных отклонений среднеарифметическое значение сдвигов равно нулю. Поэтому используются среднеквадратичные расстояния, проходимые частицей:
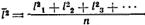
Эйнштейн и Смолуховский, постулируя единство природы броуновского движения и теплового движения, установили количественную связь между средним сдвигом частицы (называемым иногда амплитудой смещения) и коэффициентом диффузии D.
Если броуновское движение является следствием теплового движения молекул среды, то можно говорить о тепловом движении частиц дисперсной фазы. Это означает, что дисперсная фаза, представляющая собой совокупность числа частиц, должна подчиняться тем же статистическим законам молекулярно-кинетической теории, приложимым к газам или растворам.
 Для установления связи между средним сдвигом (смещением) частицы и коэффициентом диффузии представим себе трубку с поперечным сечением S, наполненную золем, концентрация частиц которого уменьшается слева направо. В этом же направлении протекает и диффузия частиц золя (на рисуике отмечено стрелкой). Выделим по обе стороны от линии MN два малых участка 1 и 2, размеры которых в направлении диффузии равны Δ — среднему квадратичному сдвигу за время τ. Обозначим частичную концентрацию золя в объемах этих участков соответственно через ν1 и ν2 (ν1>ν2). Хаотичность теплового движения приводит к равной вероятности переноса дисперсной фазы из обоих объемов вправо и влево от линии MN: половина частиц переместится вправо, а другая половина — влево. Количество дисперсной фазы за время τ переместится из объема 1 вправо:
Для установления связи между средним сдвигом (смещением) частицы и коэффициентом диффузии представим себе трубку с поперечным сечением S, наполненную золем, концентрация частиц которого уменьшается слева направо. В этом же направлении протекает и диффузия частиц золя (на рисуике отмечено стрелкой). Выделим по обе стороны от линии MN два малых участка 1 и 2, размеры которых в направлении диффузии равны Δ — среднему квадратичному сдвигу за время τ. Обозначим частичную концентрацию золя в объемах этих участков соответственно через ν1 и ν2 (ν1>ν2). Хаотичность теплового движения приводит к равной вероятности переноса дисперсной фазы из обоих объемов вправо и влево от линии MN: половина частиц переместится вправо, а другая половина — влево. Количество дисперсной фазы за время τ переместится из объема 1 вправо:  , а из объема 2 влево (в обратном направлении):
, а из объема 2 влево (в обратном направлении): 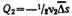 .
.
Так как |Q1| > |Q2| (ν1>ν2), то суммарное количество перенесенного вещества через плоскость MN вправо определится соотношением  .
.
Градиент концентрации по расстоянию в направлении диффузии можно выразить так:

Подставляя, получим: 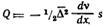
Сравнивая это соотношение с первым законом диффузии Фика:  , окончательно имеем:
, окончательно имеем:

Это уравнение выражает закон Эйнштейна — Смолуховского, в соответствии с которым квадрат среднего сдвига пропорционален коэффициенту диффузии н времени.
3. Используя данные по адсорбции этана на поверхности однородной графитированной сажи при постоянной степени заполнения, рассчитайте изостерическую теплоту адсорбции:
| P, Па | Т, К |
| 25,1 | |
| 15,2 | |
| 9,8 | |
| 5,6 | 153,8 |

 2017-12-16
2017-12-16 1740
1740








