Вычисление определителей на основании их свойств, например:
26. Числа 24026, 40262, 02624, 26240, 62402 делятся на 41. Докажите, что на 41 делится определитель  .
.
27. Методом рекуррентных соотношений вычислите определитель Вандермонда 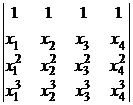 .
.
28. Вычислить следующие определители:
а)  ; б)
; б)  ;
;
в)  ;
;
29. При помощи теоремы Лапласа вычислите определитель
 .
.
Решение систем линейных уравнений, например:
30. Решите матричные уравнения, используя обратную матрицу:
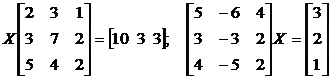 .
.
Исследование на линейную зависимость элементов линейного пространства, например:
31. Исследуйте на линейную зависимость систему матриц:
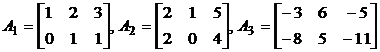 .
.
32. Докажите линейную зависимость функций

33. Докажите линейную независимость функций
а)  ;б)
;б)  ; в)
; в) 
Составление матрицы перехода, например:
34. Запишите матрицу перехода от базиса  к базису
к базису  .
.
35. Запишите матрицу перехода от базиса
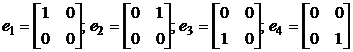
к базису  .
.
Определение линейного оператора и его матрицы, например:
36. Проверьте, будет ли отображение  линейным оператором, если
линейным оператором, если  , где – некоторый фиксированный вектор. Если является, запишите его матрицу в базисе
, где – некоторый фиксированный вектор. Если является, запишите его матрицу в базисе 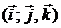 при
при  .
.
|
|
|
37. Покажите, что в трехмерном линейном пространстве следующие операторы являются линейными и запишите матрицу каждого из них в базисе 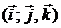 :
:
а) симметрии относительно плоскости  ; б) симметрии относительно оси
; б) симметрии относительно оси  ; в)симметрии относительно начала координат; г) проектирования на плоскость
; в)симметрии относительно начала координат; г) проектирования на плоскость  ; д) проектирования на ось
; д) проектирования на ось  .
.
Вычисление собственных значений и собственных векторов, приведение квадратной матрицы к диагональному виду, например:
38. Найдите собственные векторы линейного оператора комплексного трехмерного линейного пространства в себя, матрица которого в некотором базисе совпадает с матрицей
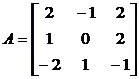
39. Для матрицы А найдите диагональный вид и невырожденную матрицу Т, приводящую А к диагональному виду, если

40. Найдите базис из собственных и присоединенных векторов линейного оператора  , матрица которого в некотором базисе пространства
, матрица которого в некотором базисе пространства  имеет вид:
имеет вид:
а) 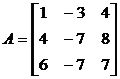 ; б)
; б)  ; в)
; в) 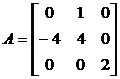
г) 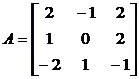 ; д)
; д)  ; е)
; е)  ;
;
ж) 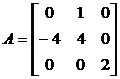 .
.
Приведение квадратичной формы к каноническому виду методом Лагранжа, например:
41. Найдите канонический вид и одно из невырожденных линейных преобразований переменных, приводящих квадратичную форму  к этому каноническому виду.
к этому каноническому виду.
Приведение к каноническому виду уравнений линий и поверхностей второго порядка, например:
42. Определите вид линии второго порядка  , приведя ее уравнение к каноническому виду. Нарисуйте эту кривую.
, приведя ее уравнение к каноническому виду. Нарисуйте эту кривую.
43. Определите вид поверхности второго порядка  , приведя ее уравнение к каноническому виду.
, приведя ее уравнение к каноническому виду.
 2017-12-16
2017-12-16 337
337








