44. Про матрицу  известно, что
известно, что  , а
, а  . Докажите, что
. Докажите, что
 .
.
45. С помощью элементарных преобразований вычислите обратную матрицу для матрицы  .
.
46. Проверьте, является ли действительным линейным пространством множество положительных действительных чисел, если в качестве внутренней операции взять умножение чисел, а в качестве внешней – возведение в степень.
47. Проверьте, являются ли действительными линейными пространствами относительно обычных операций сложения матриц и умножения матриц на действительное число следующие множества матриц:
а)  ; б)
; б) 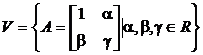
в)  .
.
Если является, найдите какой-либо базис этого пространства и укажите его размерность.
48. Проверьте, являются ли действительными линейными пространствами относительно обычных операций сложения функций и умножения функций на действительное число следующие множества функций:
а)  ; б)
; б)  :
:
в)  .
.
49. Пусть  . Проверьте, является ли
. Проверьте, является ли  линейным пространством относительно следующих операций сложения и умножения на действительное число:
линейным пространством относительно следующих операций сложения и умножения на действительное число:
|
|
|
а)  ;
;
б) 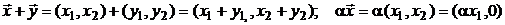 .
.
50. Проверьте, будет ли отображение  линейным оператором, если
линейным оператором, если 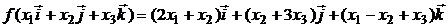 . Если да, запишите его матрицу в базисе
. Если да, запишите его матрицу в базисе 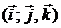 .
.
51. Проверьте, будет ли отображение  линейным оператором, если
линейным оператором, если  . Если да, запишите его матрицу в базисе
. Если да, запишите его матрицу в базисе 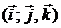 .
.
52. Проверьте, будет ли отображение  линейным оператором, если
линейным оператором, если  . Если да, запишите его матрицу в базисе
. Если да, запишите его матрицу в базисе 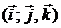 .
.
53. Покажите, что отображение  пространства матриц второго порядка в себя является линейным и запишите его матрицу в базисе
пространства матриц второго порядка в себя является линейным и запишите его матрицу в базисе
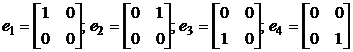 ,
,
если для каждой квадратной матрицы Х второго порядка: а)  , б)
, б)  , где
, где 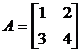 .
.
54. В базисе  пространства многочленов степени не выше двух матрица линейного оператора имеет вид
пространства многочленов степени не выше двух матрица линейного оператора имеет вид  . Запишите его матрицу в базисе
. Запишите его матрицу в базисе  .
.
55. Найдите базис из собственных и присоединенных векторов линейного оператора  , матрица которого в некотором базисе совпадает с матрицей
, матрица которого в некотором базисе совпадает с матрицей  , если
, если  .
.
56. Найдите ортогональное преобразование переменных, приводящее квадратичную форму к каноническому виду, и запишите этот канонический вид для следующих квадратичных форм: а)  ; б)
; б)  .
.
57. Выясните, при каких значениях параметра 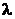 квадратичная форма положительно определена и при каких
квадратичная форма положительно определена и при каких 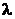 она отрицательно определена для следующих квадратичных форм:
она отрицательно определена для следующих квадратичных форм:
а)  ;
;
б)  .
.
58. Определите вид линии второго порядка 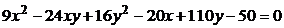 , приведя ее уравнение к каноническому виду. Нарисуйте эту кривую.
, приведя ее уравнение к каноническому виду. Нарисуйте эту кривую.
59. Определите вид поверхности второго порядка  , приведя ее уравнение к каноническому виду.
, приведя ее уравнение к каноническому виду.
60. Определите вид поверхности второго порядка  , приведя ее уравнение к каноническому виду.
, приведя ее уравнение к каноническому виду.
61. В пространстве многочленов степени не выше двух скалярное произведение задано формулой 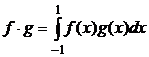 . При помощи процесса ортогонализации постройте в этом пространстве ортонормированный базис, исходя из базиса
. При помощи процесса ортогонализации постройте в этом пространстве ортонормированный базис, исходя из базиса  .
.
|
|
|
62. В базисе 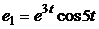 ,
,  линейного пространства
линейного пространства 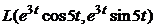 запишите матрицы линейных операторов а) дифференцирования
запишите матрицы линейных операторов а) дифференцирования  (
( ); б) второго дифференцирования
); б) второго дифференцирования 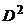 (
( ).
).
Для получения оценки девять могут быть предложены более сложные задачи.
 2017-12-16
2017-12-16 262
262







