2017-12-16
284
Операции над матрицами: сложение, вычитание, умножение на число, умножение, транспонирование, возведение в степень, многочлен от матрицы. Например:
1. Заданы матрицы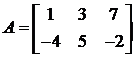 
, 
, 
, 
.
Из перечисленных операций выполнить те, которые определены:
а) 
, б) 
, в) 
, г) 
.
2. Найдите сумму матриц 
, разность матриц 
и произведение матриц 
и 
, если они существуют:
.
3. Заданы матрицы:
, 
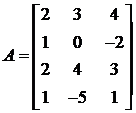и 
.
Выяснить, какие из произведений 
, 
, 
, 
, 
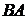или 
существуют, и найти эти произведения.
4. Для матриц 
и 
найдите те из произведений, , , 
, 
, 
, 
, 
и 
, которые существуют:
.
5. Найдите произведение матриц , если:
.
6. Найдите 
и 
, если
, 
, 
.
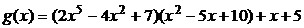Вычисление определителей третьего и четвертого порядков с помощью элементарных преобразований, например:
7. Вычислите определитель 
.
8. Вычислить следующие определители:
а) 
; б) 
.
9. Проверить, является ли невырожденной матрица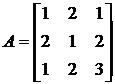 
.
Вычисление обратной матрицы второго и третьего порядка с помощью алгебраических дополнений, например:
10. Найти матрицу, обратную к невырожденной матрице второго порядка 
.
11. Используя алгебраические дополнения, найдите обратную матрицу для матрицы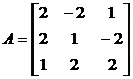 
.
Решение систем линейных уравнений матричным методом, по правилу Крамера и методом исключения неизвестных (методом Гаусса), например:
12. Решите матричные уравнения при помощи обратной матрицы:
.
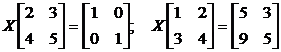13. Пользуясь правилом Крамера, решите систему уравнений (может быть и три неизвестных) 
.
14. Исследуйте на совместность систему линейных уравнений. Если она совместна, найдите ее общее и какое-либо частное решение. Сделайте проверку частного решения.
а) 
б) 
15. Для однородной системы линейных уравнений
найдите общее решение и какую-либо фундаментальную систему решений.
Вычисление ранга матрицы и матричный критерий исследования линейной зависимости, например:
16. Найдите ранг матрицы 
.
17. При помощи матричного критерия исследуйте на линейную зависимость систему векторов
.
Составление матрицы перехода, например:
18. Запишите матрицу перехода от базиса 
к базису 
.
Нахождение собственных векторов. Приведение квадратной матрицы третьего порядка к диагональному виду в случае простых корней, например:
19. В некотором базисе трехмерного пространства 
линейный оператор 
имеет матрицу 
. Проверьте, какие из векторов 
, 
и 
будут собственными векторами этого оператора и укажите их собственные значения.
20. Для матрицы А найдите диагональный вид и невырожденную матрицу Т, приводящую А к диагональному виду, если
.
21. Найдите собственные векторы линейного оператора 
, который в некотором базисе действительного линейного пространства V 3 имеет матрицу
а) 
; б) 
.
Приведение квадратичной формы к каноническому виду методом Лагранжа, например:
22. При помощи метода Лагранжа найдите канонический вид и одно из невырожденных линейных преобразований переменных, приводящих квадратичную форму 
к этому каноническому виду.
Исследование на знакоопределенность квадратичной формы по критерию Сильвестра, например:
23. Исследуйте на знакоопределенность квадратичную форму:
а) ; б) 
;
в) 
.
