Пример выполнения работы. Задача 1. Закрытая транспортная задача

 

Задача 1. Закрытая транспортная задача.

По номеру варианта Nv=30 из табл.1 приложений выпишем матрицу удельных транспортных затрат при перевозке груза от 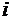-го поставщика к -му потребителю .

 

Матрица удельных транспортных расходов

 

Из табл.2 приложений выпишем запасы товара на складах а₁=60, а₂=200, а₃=50 и потребности магазинов в этом товаре b₁=110, b₂=60, b₃=110, b₄=30. Выписываем математическую модель в форме задачи ЛП о минимизации суммарных затрат на перевозки при условии, что потребности всех потребителей должны быть удовлетворены:

 

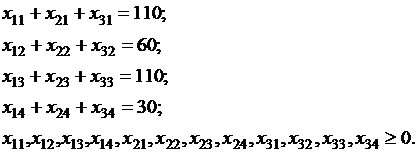(2)

Вызываем на счет файл lr3.xls.лист1, вводим исходные данные, в соответствии с системой (2) и получаем оптимальное решение:

 

Матрица плана перевозок
						А1
						А2
						А3
					Z
B1	B2	B3	B4
Матрица удельных транспортных расходов

Таким образом,

 

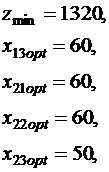
Следовательно, минимальная стоимость перевозок в размере 1320 руб. будет получена, если с 1-го склада будет отправлено в III магазин 60 ед. товара; со 2-го склада – 60 ед. в I магазин, 60 ед. во II магазин, 50 ед. в III магазин и 30 ед. в IV магазин; с 3-го склада – 50 ед. в I магазин.

Задача 2. Транспортная задача с избыточным спросом.

Из табл.3 приложений выпишем запасы товара на складах а₁=50, а₂=150, а₃=40 и потребности магазинов в этом товаре b₁=110, b₂=180, b₃=150, b₄=80. Получаем:

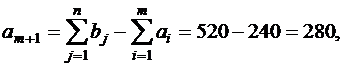выполняется неравенство - транспортная задача называется открытой транспортной задачей с избыточным спросом. Приведём её к закрытой задаче, введя в рассмотрение условного поставщика , величина запасов у которого: а удельные транспортные затраты по перевозке груза от условного поставщика ко всем потребителям принимаются равными 0: (реально перевозки не производятся).

Математическая модель задачи:

 

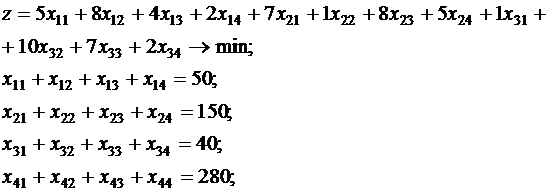
(3)

 

Вызываем на счет файл lr3.xls.лист2, вводим исходные данные, в соответствии с системой (3) и получаем оптимальное решение:

 

Матрица плана перевозок
						А1
						А2
						А3
						A4
B1	B2	B3	B4		Z
Матрица удельных транспортных расходов

 

Получим следующие результаты:

 

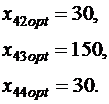
Минимальная стоимость перевозок в размере 290 руб. будет получена, если с 1-го склада будет отправлено в IV магазин 50 ед. товара; со 2-го склада во II магазин- 50 ед.; с 3-го склада – 40 ед. в I магазин. При этом I магазин недополучит 70 ед. товара; II магазин - 30 ед. товара; III магазин - 150 ед. товара; IV магазин - 30 ед. товара.

 

 

Задача 3. Транспортная задача с избыточным предложением.

 

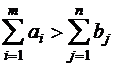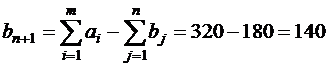Из табл.4 приложений находим, что запасы товара на складах а₁=160, а₂=70, а₃=90, а потребности магазинов в этом товаре b₁=50, b₂=30, b₃=70, b₄=30. Получаем: выполняется неравенство - транспортная задача называется открытой транспортной задачей с избыточным предложением. Приведём её приведена к закрытой задаче, если ввести в рассмотрение условного потребителя , величина запасов у которого: , а удельные транспортные затраты по перевозке груза от условного поставщика ко всем потребителям принимаются равными 0: (реально перевозки не производятся).

Запишем математическую модель задачи:

(4)

 

Вызываем на счет файл lr3.xls.лист2, вводим исходные данные, в соответствии с системой (4) и получаем оптимальное решение:

 

Матрица плана перевозок
							А1
							А2
							А3
						Z
B1	B2	B3	B4	B5
Матрица удельных транспортных расходов

 

Получим следующие результаты:

Минимальная стоимость перевозок в размере 620 руб. будет получена, если с 1-го склада будет отправлено в I магазин 50 ед. товара и в III магазин – 70 ед. товара; со 2-го склада во II магазин- 30 ед.; с 3-го склада – 30 ед. в IV магазин. При этом на складе1 останется 40 ед. товара; на складе 2 - 40 ед. товара; на складе 3 - 60 ед. товара.

 

Контрольные вопросы

1. Как формулируется транспортная задача; записать математическую модель закрытой транспортной задачи?

2. Записать математическую модель открытой транспортной задачи? Как привести открытую транспортную задачу к закрытой?

3. Каков экономический смысл фиктивных поставщика и потребителя?

ПРИЛОЖЕНИЕ

Таблица1.

 

Nv

a11

a12

a13

a14

a21

a22

a23

a24

a31

a32

a33

a34

 

 

Таблица 2.

Nv	a1	a2	а3	b1	b2	b3	b4

 

 

Таблица 3.

 

Nv	a1	a2	а3	b1	b2	b3	b4

 

 

Таблица 4.

 

Nv	a1	a2	а3	b1	b2	b3	b4

Лабораторная работа №4

Решение задач линейного программирования с помощью пакета электронных таблиц EXСEL

 

Цель: научиться решать оптимизационные задачи ЛП с помощью электронных таблиц EXСEL.

 

Задание: предприятие может выпускать 5 видов продукции, для их выпуска используются 4 вида ресурсов, запасы которых соответственно равны b₁, b₂, b₃, b_4. Расходы ресурсов для производства данных видов продуктов заданы с помощью технологической матрицы производства А. Известны цены реализации продукции с₁, с₂, с₃, с₄, с₅. Необходимо составить план производства, приносящий максимальную прибыль.