Целочисленная задача линейного программирования о распиле

 

Цель: научиться строить математические модели целочисленных экономических задач в форме задач линейного программирования и решать их с помощью ЭВМ.

 

Задание: записать задачу об оптимальном распиле A бревен длиной 3 м, обеспечивающем образование максимального числа комплектов, состоящих из брусков m размеров a₁,…, a_m, которые в комплекте находятся в пропорции k₁:k₂:k₃ в виде задачи целочисленного линейного программирования и решить их с помощью ЭВМ.

Краткие теоретические положения

 

Имеется А брёвен длиной по 3м. Их необходимо распилить на бруски m размеров a₁,…, a_m. Из брусков образуют комплекты, количество брусков в которых к₁,…, к_m. Определить, какое количество бревен, и по какому способу необходимо распилить для образования максимального количества комплектов.

Пусть имеется n способов распила бревен на бруски и х₁,…, х_n- количество бревен, распиленных по каждому способу, а х_n+1- количество полученных комплектов.

Математическая модель задачи:

(1),

где - количество бревен, распиленных всеми способами;

- количество брусков размера , выпиливаемых из бревна при 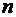-ном способе распила;

- количество брусков размера а_m, выпиливаемых всеми возможными способами;

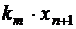- количество брусков размера а_m, входящих во все комплекты

 

Индивидуальное задание

Имеется А брёвен длиной по 3м. Их необходимо распилить четырьмя различными способами на бруски 3-х размеров a₁, а₂, а₃. Из брусков образуют комплекты, количество брусков в которых к₁, к₂, к₃. Определить, какое количество бревен, и по какому способу необходимо распилить для образования максимального количества комплектов.

Числовые параметры индивидуального задания определяются по номеру варианта Nv из таблицы 1 приложений.

 

Пример выполнения работы

 

Nv=30- номер варианта.

 

Для решения задачи строим математическую модель задачи. Из таблицы 1 приложений: A=100, a₁=0.6, a₂=1.5, a₃=2.5, k₁=2, k₂=1, k₃=3.

Определим 4 возможных способа распила бревен длиной 3 м на брусья указанной длины, при каждом способе бревно должно использоваться максимально, т.е. нельзя из остатка выпилить хотя бы один дополнительный брусок. Все эти способы приведены в таблице:

 

Номер способа распила	Количество брусьев 0.6 м	Количество брусьев 1.5 м	Количество брусьев 2.5 м

 

Таким образом, для данного набора трех типов брусков определили 4 возможных способа распила одного бревна длиной 3 м. Поставим в соответствие каждому способу x_i неизвестную величину x_i, 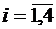, где x_i- количество бревен, распиленных по способу i. Пусть x₅- количество образованных комплектов их брусков, полученных после распиливания бревен. Получаем задачу ЦЛП:

z=x₅® max – количество комплектов;

x₁+x₂+x₃+x₄£ 100 – общее количество распиленных бревен;

5x₁+2x₂ 2x₅ - количество брусков по 0.6 м;

x₂+2x₃ x₅ - количество брусков по 1.5 м;

x₄ 3x₅ - количество брусков по 2.5 м;

x₁, x₂, x₃, x₄³0 – условие неотрицательности;

x₁, x₂, x₃, x₄- целые - условие целочисленности.

или:

z=x₅® max;

x₁+x₂+x₃+x₄£ 100;

5x₁+2x₂-2x₅³0;

x₂+2x₃-x₅³0;

x₄-3x₅³0;

x₁, x₂, x₃, x₄³0;

x₁, x₂, x₃, x₄-целые.

 

Величина x₁+x₂+x₃+x₄ равна количеству распиленных бревен, поэтому первое ограничение возникло в силу ограниченности имеющегося запаса бревен числом A=100. Второе ограничение образовано с использованием таблицы, где приведены все возможные способы распила бревна длиной 3 м на бруски заданных размеров. При этом число 5x₁+2x₂ равно количеству брусков длиной 0.6 м, образовавшихся в результате распила, а число 2x₅=k₁x₅- это количество брусков данного типа, содержащихся во всех комплектах. Ограничение 5x₁+2x₂-2x₅³0 показывает количество брусков длиной 0.6 м не вошедших в состав комплектов, т.е. пошедших в остаток. Аналогичный смысл имеют третье и четвертое ограничения. Пятое ограничение - условие неотрицательности переменных. Наконец, шестое ограничение- условие целочисленности, означающее, что количества распиленных брёвен x₁, x₂, x₃, x₄- должны быть целыми числами.

 

Запускаем файл lr2.xls и после завершения работы программы ‘Поиск решения’, получаем

переменные	x1	x2	x3	x4	x5
значения
нижняя граница						Тип задачи
верхняя граница						z	max
целевая функция
	целое	целое	целое	целое	целое
Ограничения	левая часть	знак	правая часть
бревна							<=
бруски 1					-2		=>
бруски 2					-1		=>
бруски 3					-3		=>

 

 

Таким образом, в оптимальном решении:

1) Получено комплектов- x₅=25;

2) Распилено бревен по

первому способу: x₁=10;

второму: x₂=1;

третьему: x₃=12;

четвертому: x₄=75;

Не распиленных бревен осталось: A- x₁- x₂- x₃- x₄=

=100-10-1-12-75=2, т.е. 2 бревна оказались не распилены;

 

3) Количество остатков (м): 3A-x₅()=

=3·100--25(2×0.6+1× 1.5+3∙2.5)=45м., где величина -общая длина брусков в одном комплекте.

При таком способе расчёта остатками считаем:

а) не распиленные брёвна;

б) бруски, не вошедшие в комплекты;

в) остатки, образующиеся после распила брёвен.

5) а) Брусков первого типа, длиной 0.6 м не вошло в комплекты

5x₁+2x₂-2x₅=5∙10+2∙1-2∙25=2;

б) Брусков второго типа, длиной 1.5 м не вошло в комплекты:

x₂+2x₃-х₅=1+2∙12-25=0;

в) Брусков третьего типа, длиной 2.5 м не вошло в комплекты

x₄-3x₅=75-3∙25=0;.

Контрольные вопросы

 

1. Какая задача линейного программирования называется целочисленной?

2. Каким образом в задаче о разрезании (распиле) определяется число возможных способов такого распила?

3. Какими параметрами определяется состав образуемых комплектов из брусков?

4. Каков критерий оптимизации в задаче о распиле (каково его экономическое содержание).

5. Каков смысл неизвестных задачи

6. Пояснить смысл каждого ограничения.

7. По каким формулам находится суммарное количество остатков м, количество оставшихся брусков каждого типа, количество не распиленных бревен, количество образованных комплектов из брусков?

 

 

ПРИЛОЖЕНИЕ

 

Nv	A	a1	a2	a3	k1	k2	k3
		0.6	2.3	1.5
			1.2
		0.8	0.6	0.4
		0.6	0.8
		1.5		1.2
		0.8	1.5	1.3
			1.5	1.3
		0.8		0.6
		1.5		0.8
		0.8		1.4
			1.3	1.5
		0.6		0.8
		0.8	1.4	0.7
			1.4
			1.4	1.6
		0.6		0.9
		0.8	1.1	0.7
		1.2	1.4
			1.8	1.5
		0.5		0.8
		0.3	1.4	0.7
			1.4
		1.6	1.3	1.5
		0.6		0.8
		0.2	1.4	0.7
		0.3	1.8	2.2
		0.4	1.5	2.6
		0.6	1.2	2.7
		0.4	1.1	2.8
		0.6	1.5	2.5

Таблица1.

Лабораторная работа №3

Классическая транспортная задача

 

Цель: научиться строить математические модели транспортных задач в форме задач линейного программирования и решать их с помощью пакета EXCEL.

Задание: записать транспортные задачи в форме задач линейного программирования и решить их с помощью пакета EXCEL.