2018-01-08
448
Предположим, имеется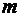 
поставщиков 
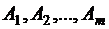, поставляющих однородный товар, причём запасы поставщиков равны 
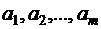. Товар поставляется 
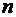потребителям 
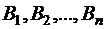, спрос которых равен 
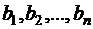. Предположим, что удельные транспортные затраты на перевозку товара от поставщика 
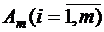к потребителю 
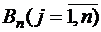составляют 
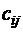денежных единиц.
Требуется определить оптимальный план поставок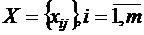 
, 
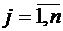при 
котором суммарные транспортные затраты должны быть минимальными.
Условие задачи можно записать в виде таблицы, которую будем называть матрицей планирования:
| C11 Х11 | … | C1n Х1n | a1 |
| … | … | … | … |
| Cm1 Хm1 | … | Cmn Хmn | am |
| b1 | … | b n |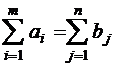 
|
Систему ограничений задачи получаем из следующих условий:
1.Все грузы должны быть вывезены, т.е.
.
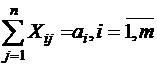2. Все потребности должны быть удовлетворены, т.е.
.
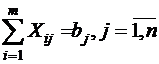3. Объёмы перевозок должны быть неотрицательными, т.е.
, .
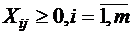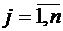Данная экономическая задача описывается математической моделью в виде задачи ЛП:
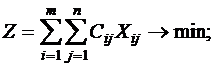
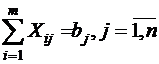; (1)
;
, .
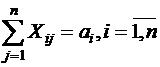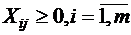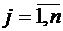Транспортная задача является задачей ЛП, т.к. требуется минимизировать линейную функцию на множестве решений системы линейных уравнений и неравенств. Ограничение 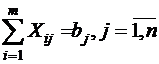, - это условие удовлетворения спроса всех потребителей, а 
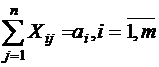, – условие реализации всех запасов поставщиков.
