Коэффициенты линейного уравнения множественной регрессии можно оценить методом наименьших квадратов (МНК). Рассмотрим процедуру их вычисления на следующем примере.
Имеются данные (в д.е.) о рыночной цене (x 1), доходе потребителя (x 2) и величине спроса (y) на некоторый товар:
| Цена (x 1) | |||||
| Доход (x 2) | |||||
| Спрос (y) |
Предположим, что между спросом, ценой товара и доходом потребителя существует линейная взаимосвязь, которая описывается уравнением:

Для расчета коэффициентов и проведения дальнейшего анализа построенного уравнения составим вспомогательную таблицу:
| Цена (x 1) |  =121 =121
| |||||
| Доход (x 2) |  =5800 =5800
| |||||
| Спрос (y) |  =3700 =3700
| |||||

| 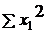 =2985 =2985
| |||||

|  =7620000 =7620000
| |||||

| И т.д. |  =82900 =82900
| ||||

|  =5130000 =5130000
| |||||

|  =135500 =135500
| |||||

| 1503,38 | 799,82 | 663,00 | 537,92 | 195,87 |  =3700 =3700
|

|  =2835,17 =2835,17
| |||||

|  =932000 =932000
| |||||

|  =56,8 =56,8
| |||||

|  =892000 =892000
|
Составим матрицу коэффициентов парной линейной корреляции:
 .
.
Здесь  ≤ 0,7. Значит, переменные х 1 и х 2 неколлинеарны. Если бы, например,
≤ 0,7. Значит, переменные х 1 и х 2 неколлинеарны. Если бы, например,  , то переменные х 1 и х 2 считались бы коллинеарными и из модели потребовалось исключить одну из них. Для этого необходимо рассмотреть коэффициенты корреляции
, то переменные х 1 и х 2 считались бы коллинеарными и из модели потребовалось исключить одну из них. Для этого необходимо рассмотреть коэффициенты корреляции  и
и  , характеризующие тесноту связи независимых переменных х 1 и х 2 с зависимым показателем у. Из уравнения в этом случае пришлось бы исключить переменную х 1, у которой связь с результирующим показателем у менее тесная, чем у фактора х 2.
, характеризующие тесноту связи независимых переменных х 1 и х 2 с зависимым показателем у. Из уравнения в этом случае пришлось бы исключить переменную х 1, у которой связь с результирующим показателем у менее тесная, чем у фактора х 2.
Для вычисления оценок неизвестных коэффициентов уравнения решим методом определителей следующую систему уравнений:
 ;
; 
 ,
,  ,
,  .
.
В результате получим модель прогноза:
 .
.
 2018-01-08
2018-01-08 931
931








