В классическом регрессионном анализе необходимо выполнение следующих предположений:
1. 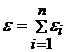 , где n число наблюдений. Величина
, где n число наблюдений. Величина 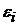 - случайная величина, откуда следует, что
- случайная величина, откуда следует, что 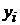 также случайная величина с распределением того же вида, что и
также случайная величина с распределением того же вида, что и 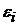 .
.
2. 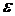 имеет нулевое математическое ожидание.
имеет нулевое математическое ожидание.
3. Значения случайной величины 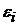 не коррелированы и имеют одинаковые дисперсии. Данное условие говорит о том, что результаты предыдущих опытов не оказывают влияния на последующие опыты. Одинаковая дисперсия говорит о том, что интенсивность случайных возмущений не изменяется ни при изменении регрессоров, но во времени, в течении которого проводятся наблюдения.
не коррелированы и имеют одинаковые дисперсии. Данное условие говорит о том, что результаты предыдущих опытов не оказывают влияния на последующие опыты. Одинаковая дисперсия говорит о том, что интенсивность случайных возмущений не изменяется ни при изменении регрессоров, но во времени, в течении которого проводятся наблюдения.
4. Случайная величина 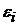 имеет нормальное распределение. Влияние множества случайных величин с примерно одинаковыми дисперсиями эквивалентно влиянию единственной случайной величины с нормальным законом распределения.
имеет нормальное распределение. Влияние множества случайных величин с примерно одинаковыми дисперсиями эквивалентно влиянию единственной случайной величины с нормальным законом распределения.
5. Матрица регрессоров MF (5) не случайна.
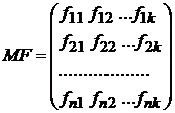 (5)
(5)
где
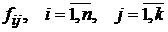 - значения регрессоров, где n – число наблюдений, k – число различных регрессоров.
- значения регрессоров, где n – число наблюдений, k – число различных регрессоров.
Все регрессоры 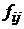 в уравнении (4) для каждого наблюдения из табл. 1 являются известными числами, точно заданные исследователем.
в уравнении (4) для каждого наблюдения из табл. 1 являются известными числами, точно заданные исследователем.
6. На значения параметров модели (4) 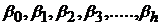 не накладывается никаких ограничений. Предварительно о значениях
не накладывается никаких ограничений. Предварительно о значениях 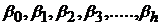 ничего не известно, следовательно, в процессе вычисления они могут получиться любыми.
ничего не известно, следовательно, в процессе вычисления они могут получиться любыми.
7. Ранг матрицы MF должен быть равен числу коэффициентов (регрессоров) модели 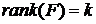 , где k – число различных регрессоров. Нарушение данного условия может быть вызвано в случае, когда число проведенных опытов меньше числа коэффициентов (
, где k – число различных регрессоров. Нарушение данного условия может быть вызвано в случае, когда число проведенных опытов меньше числа коэффициентов (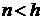 ), либо определено для ситуации (
), либо определено для ситуации (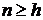 ), что между некоторыми столбцами матрицы MF существовала линейная зависимость.
), что между некоторыми столбцами матрицы MF существовала линейная зависимость.
Виды регрессии
При помощи регрессионного анализа можно получить два типа моделей:
- Линейная модель регрессии 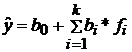 , в том случае, когда функция регрессии линейна относительно параметров модели
, в том случае, когда функция регрессии линейна относительно параметров модели  , то есть коэффициенты
, то есть коэффициенты  должны быть линейными. При этом модель не обязательно линейна относительно
должны быть линейными. При этом модель не обязательно линейна относительно 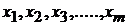 .
.
- Нелинейная модель регрессии (например 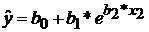 ) в том случае, когда функция регрессии не линейна относительно параметров
) в том случае, когда функция регрессии не линейна относительно параметров  .
.
Различают два типа функциональной зависимости 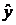 от
от 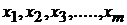 :
:
1. Парная регрессия 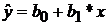 , выраженная как взаимосвязь между
, выраженная как взаимосвязь между 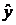 и одной независимой переменной
и одной независимой переменной 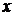 .
.
2. Множественная регрессия 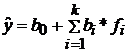 , выражается как взаимосвязь между
, выражается как взаимосвязь между 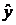 и несколькими независимыми переменными
и несколькими независимыми переменными 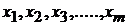 .
.
В зависимости от знака коэффициентов  различают следующие виды связи между
различают следующие виды связи между 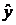 и каждым регрессором
и каждым регрессором 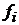 :
:
1. Положительная взаимосвязь. Если для 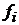 знак коэффициента
знак коэффициента  положительный, то наблюдается положительная взаимосвязь между
положительный, то наблюдается положительная взаимосвязь между 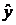 и
и 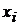 (повышение
(повышение 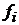 приводит к увеличению
приводит к увеличению 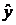 ).
).
2. Отрицательная взаимосвязь. Если для 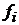 знак коэффициента
знак коэффициента  отрицательный, то наблюдается отрицательная взаимосвязь между
отрицательный, то наблюдается отрицательная взаимосвязь между 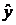 и
и 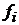 (повышение
(повышение 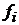 приводит к уменьшению
приводит к уменьшению 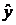 ).
).
3. Сильная взаимосвязь. В том случае, когда  имеет достаточно большое значение, то говорят о сильной взаимосвязи
имеет достаточно большое значение, то говорят о сильной взаимосвязи 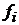 и
и 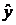 .
.
4. Слабая взаимосвязь. При значении  в пределах близких к 0, говорят о слабой взаимосвязи
в пределах близких к 0, говорят о слабой взаимосвязи 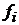 и
и 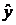 .
.
По характеру отношений между 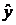 и
и 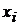 регрессия может быть:
регрессия может быть:
1. Непосредственная регрессия, когда 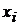 оказывает прямое воздействие на
оказывает прямое воздействие на 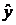 .
.
2. Косвенная регрессия, когда 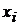 оказывает воздействие на
оказывает воздействие на 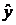 через другие факторы.
через другие факторы.
 2018-01-08
2018-01-08 1146
1146








