Точка А называется точкой разрыва функции F(x), если в этой точке функция не является непрерывной.
Пусть f(x) является непрерывной в точке А, возможны 4 случая:
1) Односторонние пределы существуют, но не равны между собой:

2) Односторонние пределы существуют, равны между собой, но не равны пределу в точке А

3) По крайней мере один предел не существует:

4) Односторонние пределы существуют, но по крайней мере один из них бесконечен
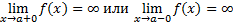
Пункты 1 и 2 - точки разрыва первого рода,
Пункты 3 и 4 - точки разрыва второго рода
Производная функции, её геометрический и механический смысл, касательная и нормаль к плоскости кривой, их уравнения.
Производной f(x) в точке x0 называется предел отношения приращения функции к приращению аргумента (при условии, что этот предел существует и конечен)

Геометрический смысл производной:
Производная функции  численно равна угловому коэффициенту касательной, проведенной в точке
численно равна угловому коэффициенту касательной, проведенной в точке  с абсциссой
с абсциссой 

Механический смысл производной:
Производная от координаты есть скорость: 
Касательная
 Касательной к
Касательной к  точке
точке  называется предельное положение секущей
называется предельное положение секущей  при стремлении точки M к точке
при стремлении точки M к точке  по кривой.
по кривой.
Уравнение касательной:

Нормалью к графику функции  в точке
в точке  прямая, проходящая через эту точку перпендикулярно касательной.
прямая, проходящая через эту точку перпендикулярно касательной.

Нормаль ⏊ касательной =>  , где k-коэффициент касательной.
, где k-коэффициент касательной.

Уравнение нормали в точке 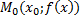 :
:

 2018-01-08
2018-01-08 892
892








