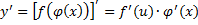Вычисление производных элементарных функций

1)

2)

3)

4)

5)

6)

7) (

8)

9)

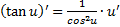
10)

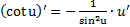
11)

12)

Связь между непрерывностью и дифференцируемостью функции, теорема о непрерывности дифференцируемой функции.

Функция называется дифференцируемой, если она имеет конечный предел в этой точке.

Теорема о связи дифференцируемости и непрерывности:

Определение 1

в

Определение 2

Функция называется дифференцируемой, если её приращение можно представить в виде: ,

Определение 1 и 2 эквивалентны.

 

52. Правила дифференцирования: производная суммы, произведения, частного, производная сложной функции, таблица производных элементарных функций.

Если

Производная суммы:

Производная произведения:

Производная частного:

Производная сложной функции:

 

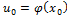
Понятие обратной функции, теорема существования и непрерывности обратной функции, теорема о производной обратной функции, вычисление производной обратных тригонометрических функций.

Определение обратной функции:
Пусть функция строго монотонная (возрастающая или убывающая) и непрерывная на области определения , область значений этой функции 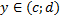, тогда на интервале определена непрерывная строго монотонная функция с областью значений , которая является обратной для .

Другими словами, об обратной функции для функции на конкретном промежутке имеет смысл говорить, если на этом интервале либо возрастает, либо убывает.

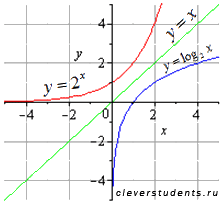
Теорема о существовании и непрерывности обратной функции:

1. Если функция f монотонна на множестве X и принимает значения на множестве Y ( 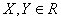), то на множестве Y определена обратная функция, принимающая значения в множестве X и обладающая тем же характером монотонности, что и сама функция f.

2. Если X=[a,b] и f монотонна и непрерывна на этом множестве, то множество значений функции f есть [f(a),f(b)] и обратная функция непрерывна на нем.

Доказательство:

Покажем, что обратная функция будет непрерывна на [f(a),f(b)].

Рассмотрим функцию : D(f)=[f(a),f(b)], E(f)=[a,b].

определена и монотонна на отрезке, множество значений – отрезок, в силу леммы 4 она непрерывна на этом отрезке.

Теорема доказана.

 

 

Производные обратных тригонометрических функций:

1)

2)

3)

4)

 

54. Гиперболические функции и их дифференцирование.

Гиперболические синус и косинус определяются как

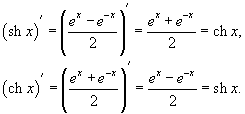Производные этих функций имеют вид:

 

Производные других (прямых и обратных) гиперболических функций: