«Замечательные пределы».
Задание 1. Пользуясь первым замечательным пределом, найти следующие пределы:
1.1. 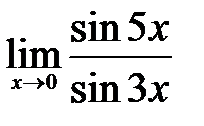 . .
| 1.2. 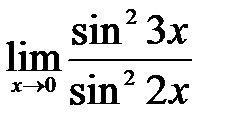 . .
| 1.3. 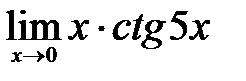 . .
|
1.4. 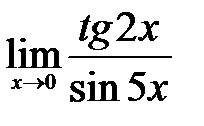 . .
| 1.5. 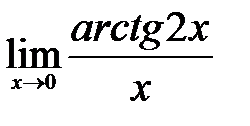 . .
| 1.6. 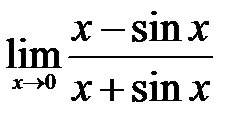 . .
|
1.7. 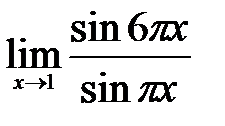 . .
| 1.8. 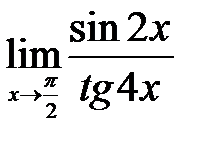 . .
| 1.9. 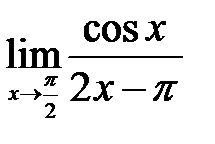 . .
|
1.10. 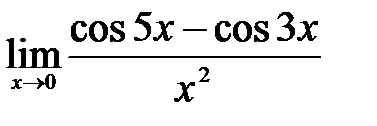 . .
| 1.11. 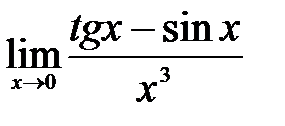 . .
| 1.12. 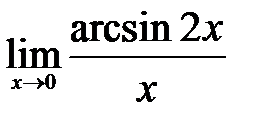 . .
|
1.13. 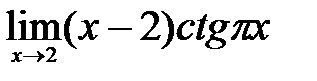 . .
| 1.14. 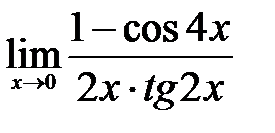 . .
| 1.15. 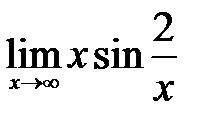 . .
|
1.16. 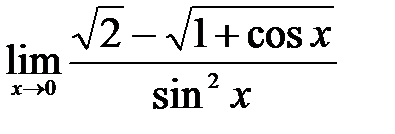 . .
| 1.17. 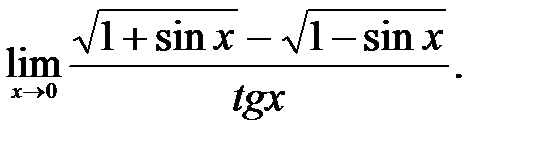
| 1.18. 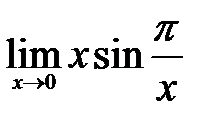 . .
|
1.19. 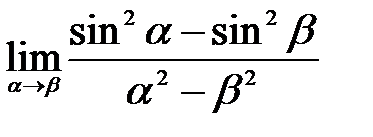 . .
| 1.20. 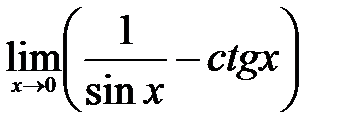 . .
| 1.21. 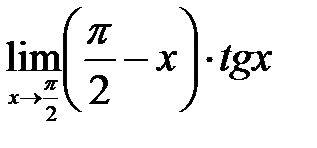 . .
|
Задание 2. Пользуясь вторым замечательным пределом, найти следующие пределы:
2.1. 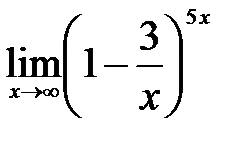 . .
| 2.2. 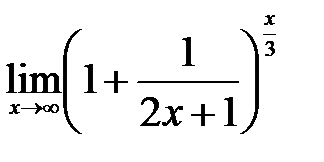 . .
| 2.3. 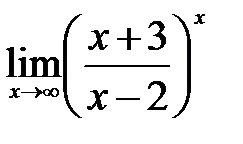 . .
|
2.4. 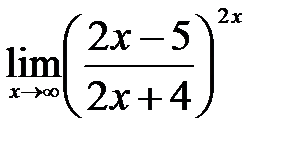 . .
| 2.5. 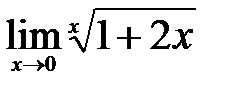 . .
| 2.6. 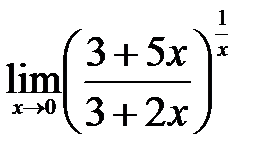 . .
|
2.7. 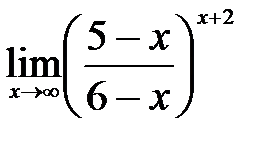 . .
| 2.8. 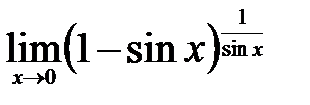 . .
| 2.9. 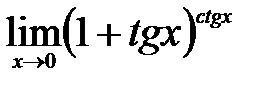 . .
|
2.10. 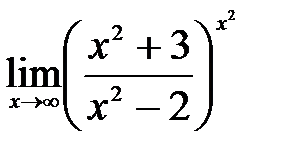 . .
| 2.11. 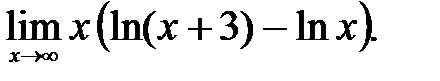
| 2.12. 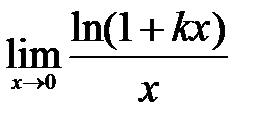 . .
|
2.13. 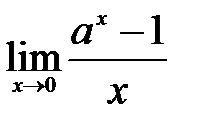 . .
| 2.14. 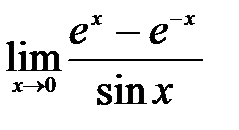 . .
| 2.15. 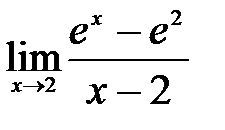 . .
|
2.16. 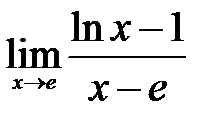 . .
| 2.17. 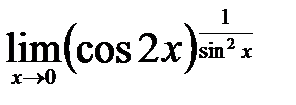 . .
| 2.18. 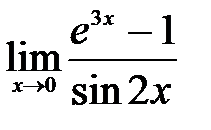 . .
|
Тема6. ЭКВИВАЛЕНТНЫЕ БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ.
Классификация бесконечно малых функций.
Определение 6.1. Пусть 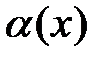 и
и 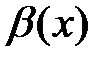 – бесконечно малые функции при
– бесконечно малые функции при 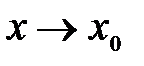 и известно, что
и известно, что 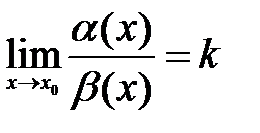 . Тогда
. Тогда
1. Если 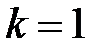 , то бесконечно малые функции
, то бесконечно малые функции 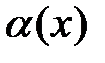 и
и 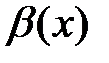 называются эквивалентными при
называются эквивалентными при 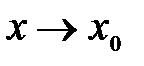 и пишут
и пишут 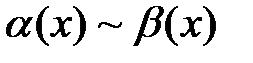 при
при 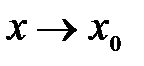 .
.
2. Если 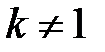 и
и 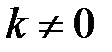 , то бесконечно малые функции
, то бесконечно малые функции 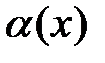 и
и 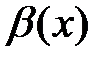 имеют одинаковый порядок малости.
имеют одинаковый порядок малости.
3. Если 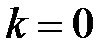 , то бесконечно малая функция
, то бесконечно малая функция 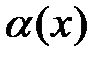 имеет более высокий порядок малости, чем функция
имеет более высокий порядок малости, чем функция 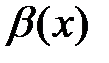 .
.
4. Если 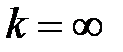 , то бесконечно малая функция
, то бесконечно малая функция 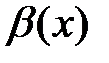 имеет более высокий порядок малости, чем функция
имеет более высокий порядок малости, чем функция 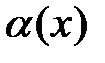 .
.
5. Если данный предел не существует, то бесконечно малые функции 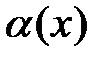 и
и 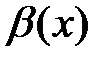 называются несравнимыми друг с другом при
называются несравнимыми друг с другом при 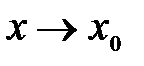 .
.
Замечание 6.1. Аналогичным образом можно сравнивать бесконечно малые функции и при 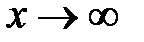 .
.
Некоторые эквивалентные бесконечно малые функциипри 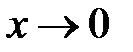 :
:
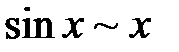
| 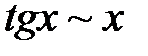
| 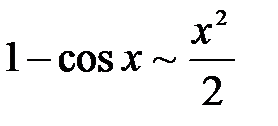
|
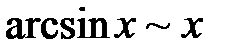
| 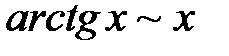
| 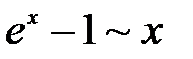
|
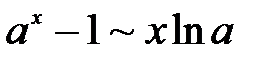
| 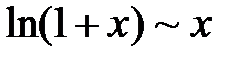
| 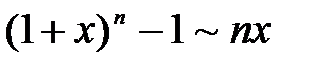
|
 2018-01-08
2018-01-08 870
870








