Для упрощения вычисления некоторых пределов можно использовать следующую теорему, основанную на эквивалентности бесконечно малых функций.
Теорема 6.1. Пусть 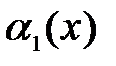 и
и 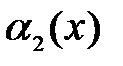 ,
, 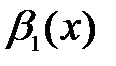 и
и 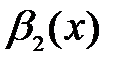 – попарно эквивалентные бесконечно малые функции при
– попарно эквивалентные бесконечно малые функции при 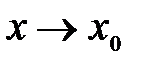 , т.е.
, т.е. 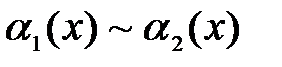 и
и 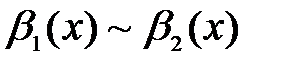 при
при 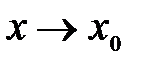 . Тогда если существует
. Тогда если существует 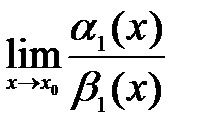 , то существует и
, то существует и 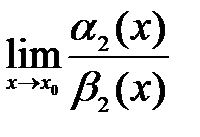 , при этом выполняется равенство
, при этом выполняется равенство 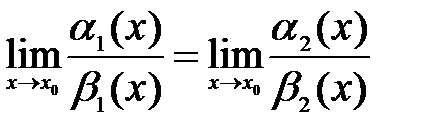 . Другими словами, предел отношения двух бесконечно малых функций не изменится, если их заменить эквивалентными бесконечно малыми функциями. Сказанное справедливо и для эквивалентных бесконечно малых функций при
. Другими словами, предел отношения двух бесконечно малых функций не изменится, если их заменить эквивалентными бесконечно малыми функциями. Сказанное справедливо и для эквивалентных бесконечно малых функций при 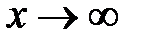 .
.
Примеры 6.1. Найти пределы, используя эквивалентные бесконечно малые:
1) 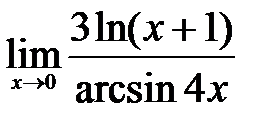 .
.
Решение: В данном примере имеем дело с отношением двух бесконечно малых функций: числитель и знаменательстремятся к нулю при 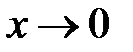 . Поэтому для вычисления предела воспользуемся эквивалентностью бесконечно малых функций:
. Поэтому для вычисления предела воспользуемся эквивалентностью бесконечно малых функций: 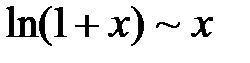 и
и 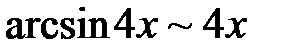 при
при 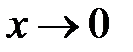 . Тогда
. Тогда
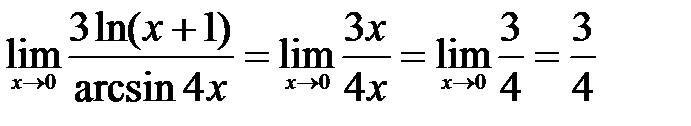 .
.
2) 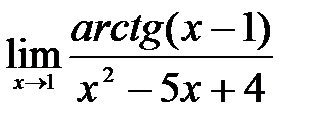 .
.
Решение: В данном примере также имеем дело с отношением двух бесконечно малых функций: числитель и знаменательстремятся к нулюпри 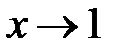 . Поэтомудля раскрытия неопределенности заменим числитель эквивалентной бесконечно малой функцией:
. Поэтомудля раскрытия неопределенности заменим числитель эквивалентной бесконечно малой функцией: 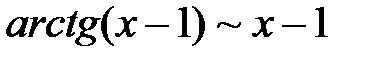 , а знаменатель разложим на множители:
, а знаменатель разложим на множители:
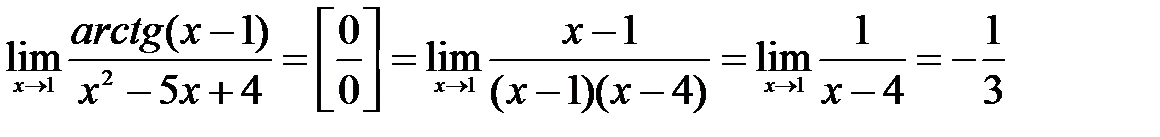 .
.
3) 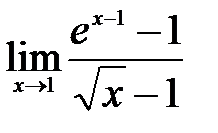 .
.
Решение: В данном примере снова имеем дело с отношением двух бесконечно малых функций: числитель и знаменательстремятся к нулюпри 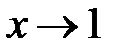 . Тогда для раскрытия неопределенности заменим числитель эквивалентной бесконечно малой функцией:
. Тогда для раскрытия неопределенности заменим числитель эквивалентной бесконечно малой функцией: 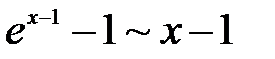 и далее воспользуемся формулой разности квадратов:
и далее воспользуемся формулой разности квадратов:
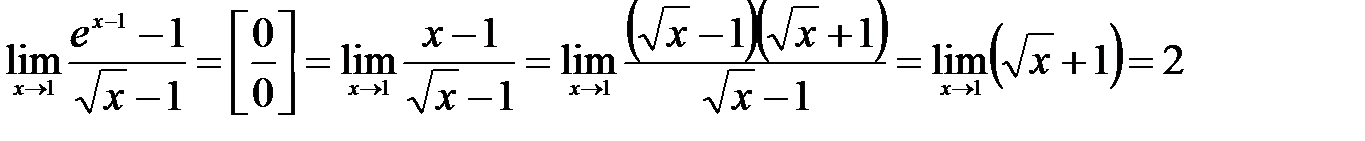 .
.
 2018-01-08
2018-01-08 1451
1451
