Второй замечательный предел. Определение 5.2.Второй замечательный предел– это предел вида

Определение 5.2. Второй замечательный предел – это предел вида

Данный предел часто используют при вычислении пределов выражений, в которых показатель степени стремится к бесконечности, а основание, за счет бесконечно малого второго слагаемого, стремится к единице, т.е. когда имеетместо неопределенность вида .

Примеры 5.2. Вычислить пределы:

1) (второй замечательный предел).

2) .

Решение: Умножим и поделим показатель степени на 2, чтобы образовать второй замечательный предел:

.

3) .

Решение: Умножим и поделим показатель степени на -6, чтобы образовать второй замечательный предел:

.

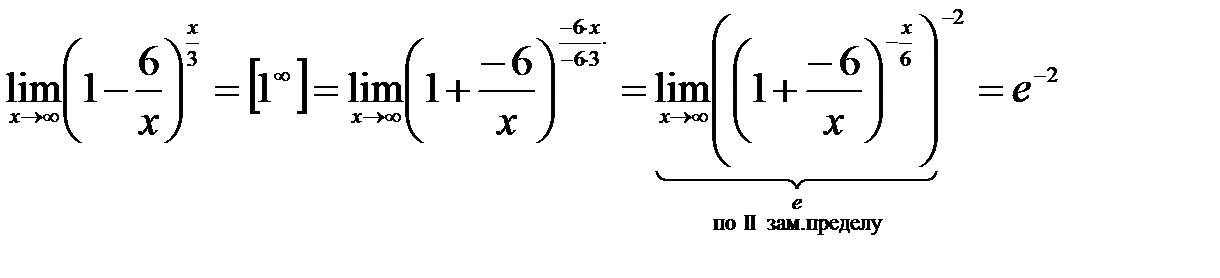4) .

Решение: Умножим и поделим показатель степени на , чтобы образовать второй замечательный предел:

В последних равенствах воспользовались соответствующей теоремой о предельном переходе и тем, что .

5) .

Решение: Так как 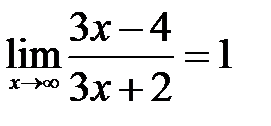и , то имеем неопределенность . Для того чтобы привести ко второму замечательному пределу, преобразуем функцию под знаком предела:

В последних равенствах воспользовались соответствующей теоремой о предельном переходе и тем, что .

6) .

Решение: При показатель степени стремится к бесконечности, а второе слагаемое суммы в скобках стремится к нулю, т.е. имеем неопределенность . Для ее раскрытия сделаем замену переменных:

.

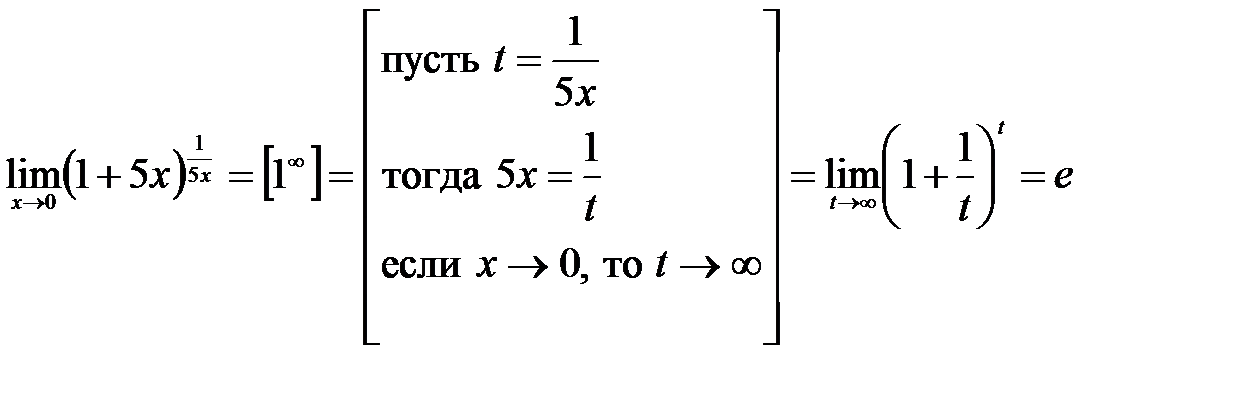7) .

Решение: Так как 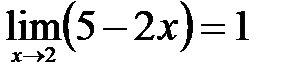, а , то имеем неопределенность . Для того чтобы привести ко второму замечательному пределу, преобразуем функцию под знаком предела к соответствующему виду, после чего сделаем замену переменных:

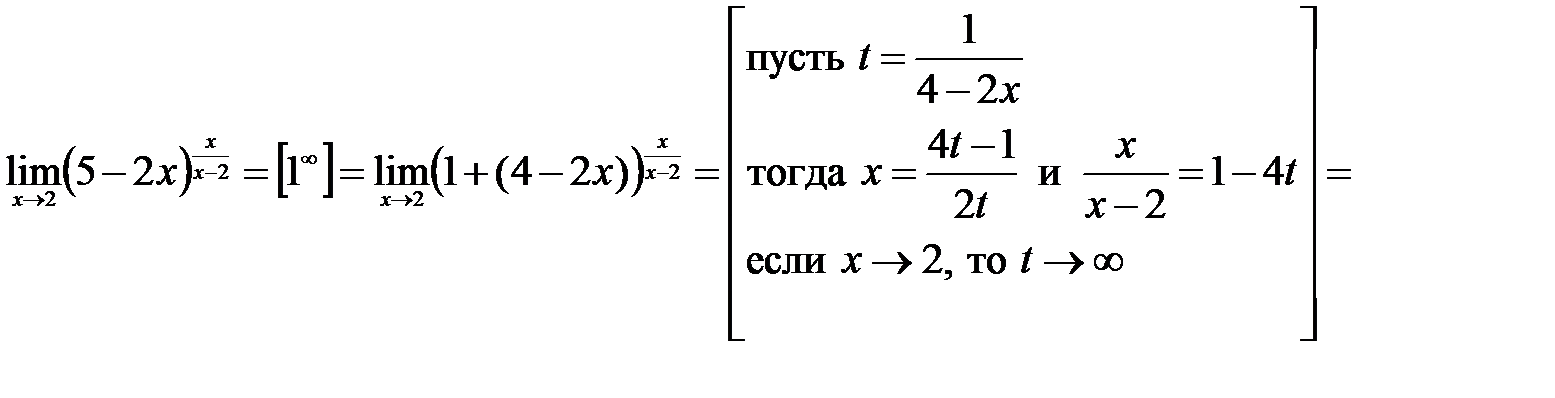
Замечание 5.2. При вычислении пределов также полезно использовать следующие следствияиз второго замечательного предела (здесь – постоянные числа):

1. .	2. .	3. .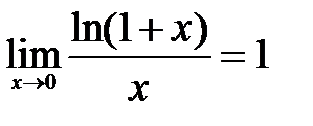
4. .	5. .