Определение 5.1. Первый замечательный предел – это предел вида
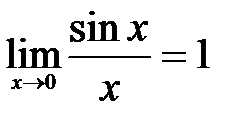 .
.
Данный предел часто используют при вычислении пределов выражений, содержащих тригонометрические функции и имеющих неопределенность 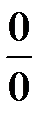 . В этих случаях с помощью преобразований выражения под знаком предела необходимо привести его к виду первого замечательного предела, т.е. к отношению синуса некоторого аргумента к этому аргументу при стремлении последнего к нулю.
. В этих случаях с помощью преобразований выражения под знаком предела необходимо привести его к виду первого замечательного предела, т.е. к отношению синуса некоторого аргумента к этому аргументу при стремлении последнего к нулю.
Примеры 5.1. Вычислить пределы:
1) 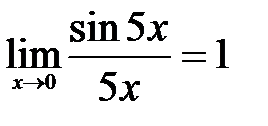 (первый замечательный предел).
(первый замечательный предел).
2) 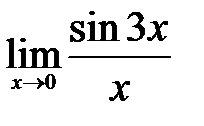 .
.
Решение: Умножим числитель и знаменатель дроби на 3, чтобы образовать первый замечательный предел:
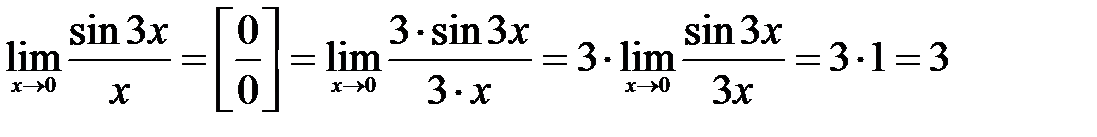 .
.
3) 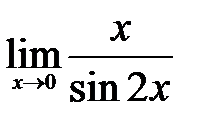 .
.
Решение: Умножим числитель и знаменатель дроби на 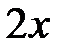 , чтобы образовать первый замечательный предел:
, чтобы образовать первый замечательный предел:
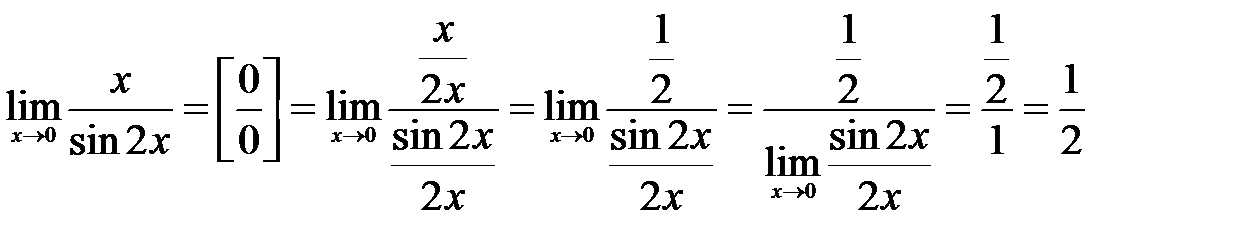 .
.
4) 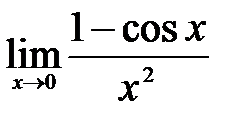 .
.
Решение: Для того чтобы образовать первый замечательный предел, сперва преобразуем числитель дроби с помощью тригонометрических тождеств:
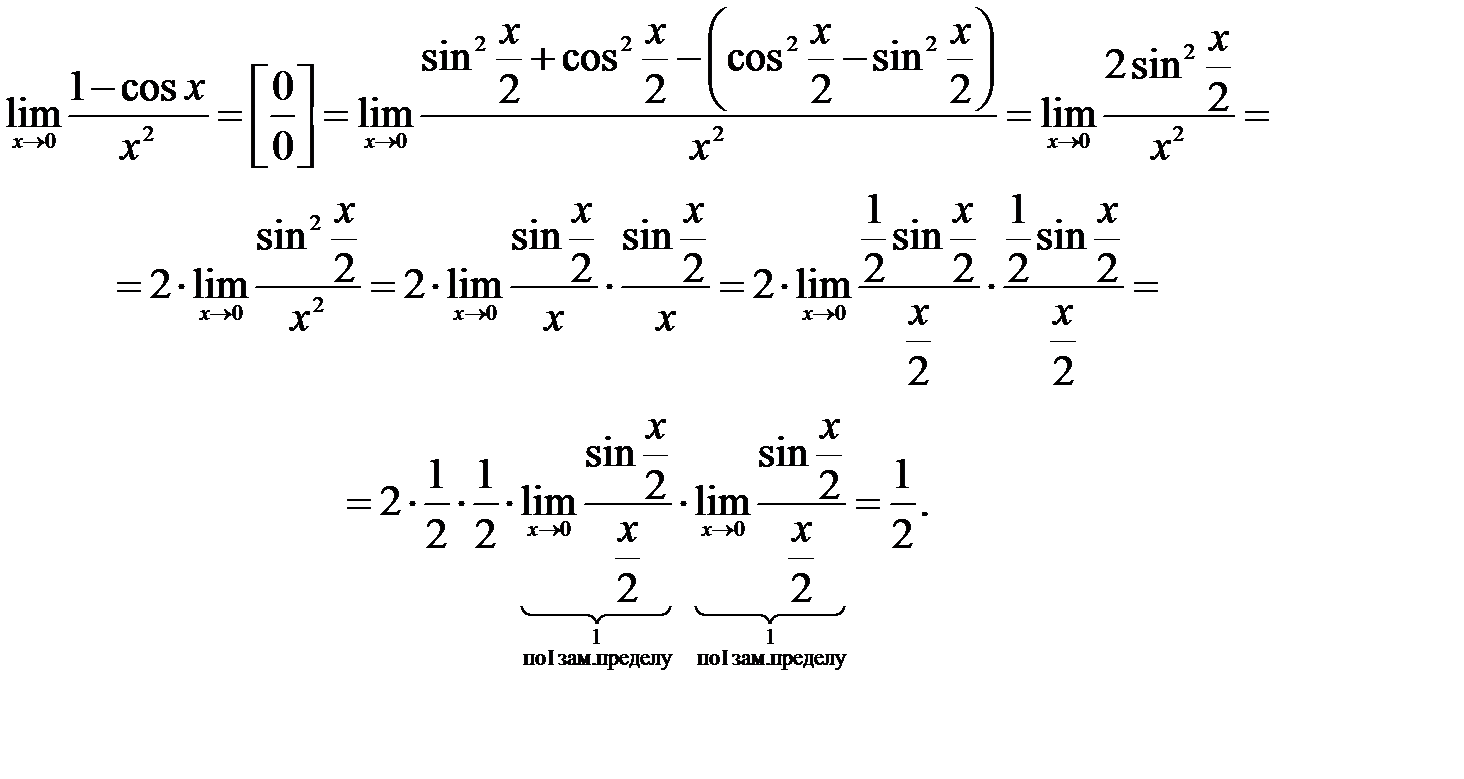
5) 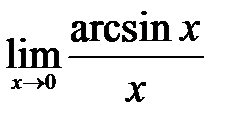 .
.
Решение: Для того чтобы привести к первому замечательному пределу, сперва сделаем замену переменных:
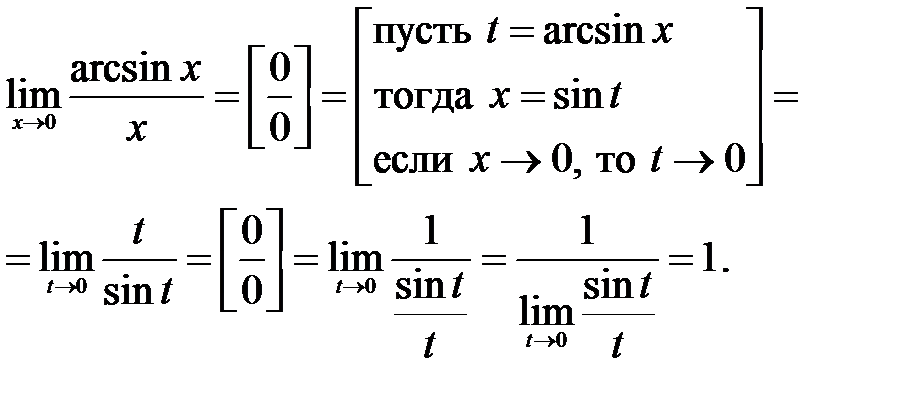
Замечание 5.1. При вычислении пределов также полезно использовать следующие следствияиз первого замечательного предела (здесь 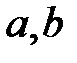 – постоянные числа):
– постоянные числа):
1. 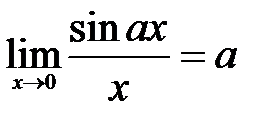 . . | 2. 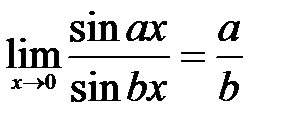 . . | 3. 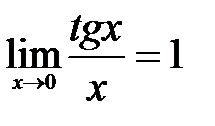 . . |
4. 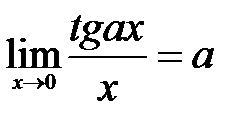 . . | 5. 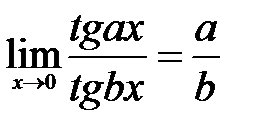 . . | 6. 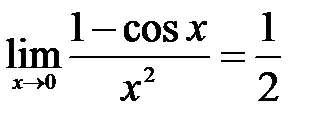 . . |
 2018-01-08
2018-01-08 1811
1811
