1) Если корни в подынтегральном выражении имеют вид 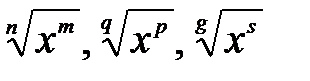 ,
,
то с помощью подстановки  , где
, где 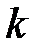 − наименьшее общее кратное показателей корней, т.е. чисел
− наименьшее общее кратное показателей корней, т.е. чисел  , подынтегральное выражение преобразуется в рациональную дробь.
, подынтегральное выражение преобразуется в рациональную дробь.
2) Интегралы вида  преобразуются в интегралы от рациональных дробей с помощью подстановки
преобразуются в интегралы от рациональных дробей с помощью подстановки  .
.
3) Интегралы вида 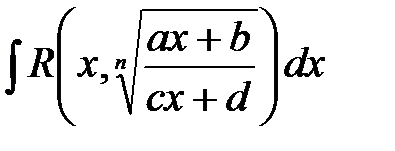 рационализируются с помощью подстановки
рационализируются с помощью подстановки  .
.
4) Интегралы вида
а)  ,б)
,б)  ,в)
,в) 
интегрируются с помощью тригонометрических подстановок:
а)  или
или 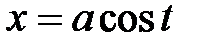 ,
,
б)  или
или  ,
,
в) 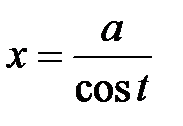 или
или  .
.
Примеры 19. Вычислить интегралы:
1) 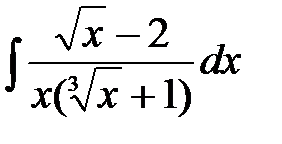 .
.
Решение: Здесь  входит в подынтегральную функцию с показателями корней 2 и 3. Поэтому применяем подстановку
входит в подынтегральную функцию с показателями корней 2 и 3. Поэтому применяем подстановку  , откуда
, откуда
 .
.
Получился интеграл от рациональной дроби. Выделяем целую часть:
 .
.
Для нахождения последнего интеграла разложим подынтегральную функцию на простейшие дроби:
 ,
,
откуда
 .
.
Приравнивая коэффициенты при одинаковых степенях  , находим
, находим  Следовательно,
Следовательно,



2) 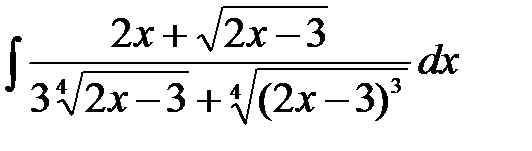 ,
,
Решение: Полагая  , имеем
, имеем


 где
где  .
.
3)  .
.
Решение: Положим 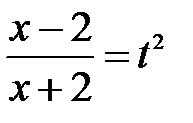 , откуда
, откуда  ,
,  .
.
Следовательно,
 .
.
Для вычисления полученного интеграла представим подынтегральную дробь в виде
 .
.
Таким образом,

 где
где  .
.
4)  .
.
Решение: Положим  . Тогда
. Тогда  ,
, 
 . Имеем
. Имеем

Так как  , то
, то  ,
,  . Поэтому
. Поэтому 
5)  .
.
Решение: Полагаем  . Откуда
. Откуда 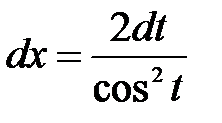 ,
, 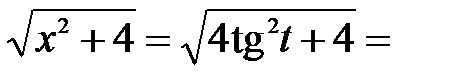
 . Следовательно,
. Следовательно,
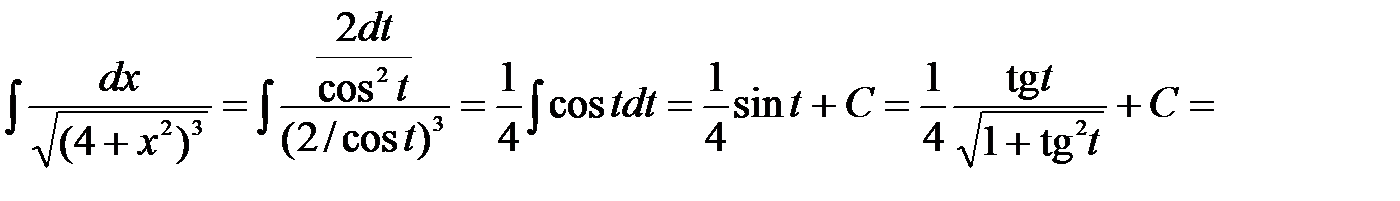

Задания для самостоятельной работы по теме
«Интегрирование иррациональных функций».
Задание. Вычислить следующие интегралы:
19.1.  . .
| 19.2.  . .
| 19.3.  . .
|
19.4.  . .
| 19.5.  . .
| 19.6.  . .
|
19.7.  . .
| 19.8.  . .
| 19.9.  . .
|
19.10.  . .
| 19.11.  . .
| 19.12.  . .
|
 2018-01-08
2018-01-08 718
718








