1) Интегралы вида 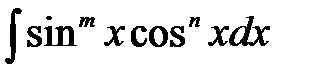 ,где
,где 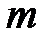 и
и 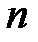 − целые числа.
− целые числа.
Рассмотрим следующие случаи:
а) Если 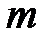 − нечетное число, то применяется подстановка
− нечетное число, то применяется подстановка 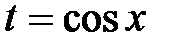 ;
;
если 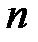 − нечетное число, то применяется подстановка
− нечетное число, то применяется подстановка 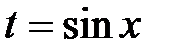 .
.
б) Если 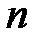 и
и 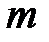 − четные неотрицательные числа, то подынтегральное выражение преобразуют с помощью формул понижения степени:
− четные неотрицательные числа, то подынтегральное выражение преобразуют с помощью формул понижения степени:
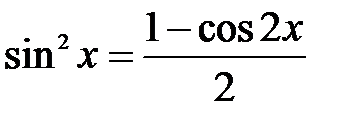 ,
, 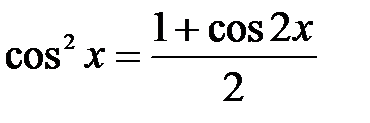 ,
, 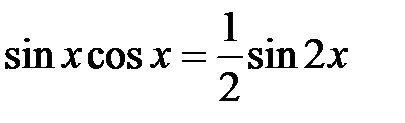 .
.
в) Если 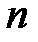 и
и 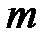 − либо оба четные, либо оба нечетные, причем хотя бы один из них отрицателен, то применяют подстановку
− либо оба четные, либо оба нечетные, причем хотя бы один из них отрицателен, то применяют подстановку 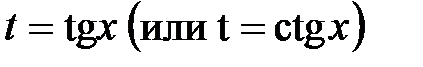 .
.
2) Интегралы вида 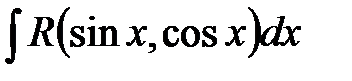 , где
, где 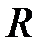 − рациональная функция.
− рациональная функция.
С помощью универсальной тригонометрической подстановки 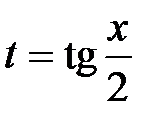 , откуда
, откуда 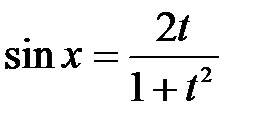 ,
, 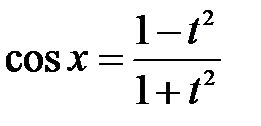 ,
, 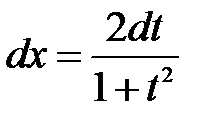 , интегралы рассматриваемого вида приводятся к интегралам от рациональных алгебраических функций.
, интегралы рассматриваемого вида приводятся к интегралам от рациональных алгебраических функций.
3) Интегралы вида 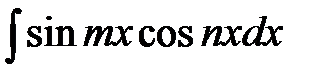 ,
, 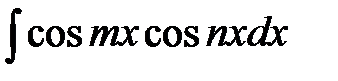 ,
, 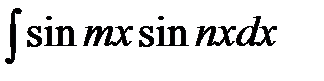 .
.
Такие интегралы легко вычисляются, если применить следующие тригонометрические формулы:
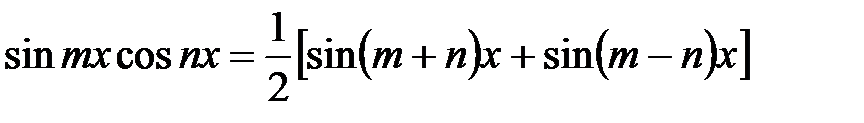 ,
, 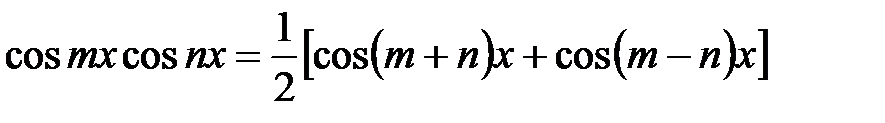 ,
,
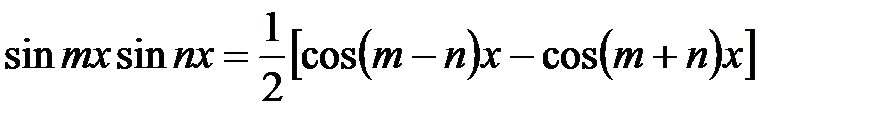 .
.
Примеры 18. Вычислить интегралы:
1) 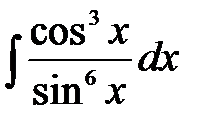 .
.
Решение: Применим подстановку 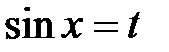 и воспользуемся формулой
и воспользуемся формулой 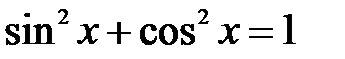 . Тогда
. Тогда
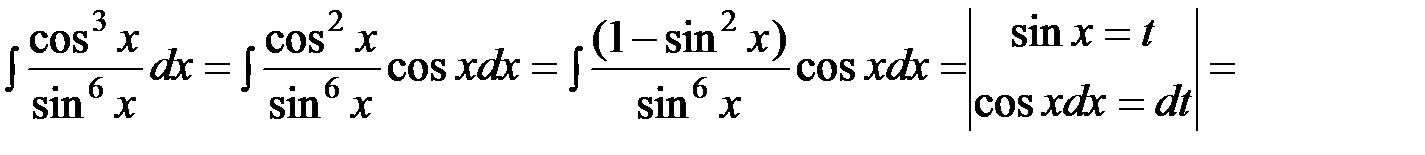
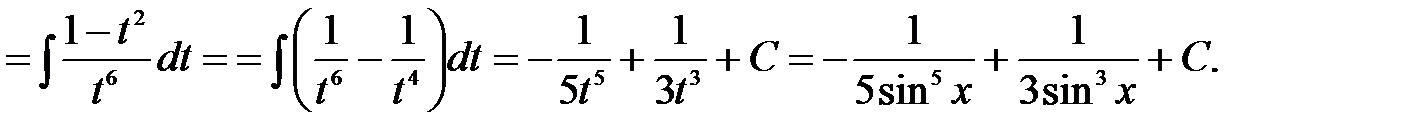
2) 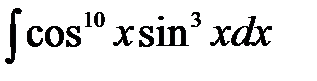 .
.
Решение: Воспользуемся подстановкой 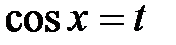 . Имеем
. Имеем
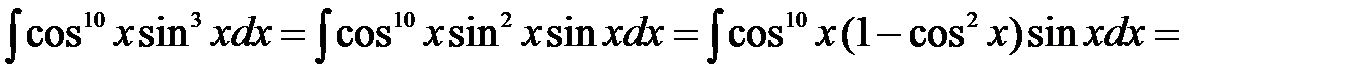
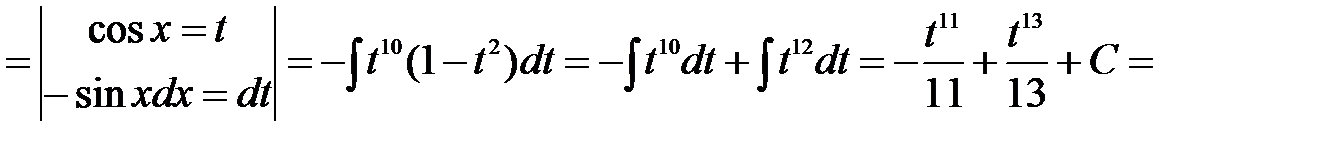
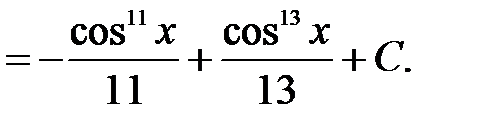
3) 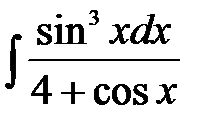 .
.
Решение: Подынтегральная функция нечетна относительно синуса, поэтому сделаем подстановку 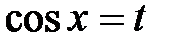 . Тогда
. Тогда
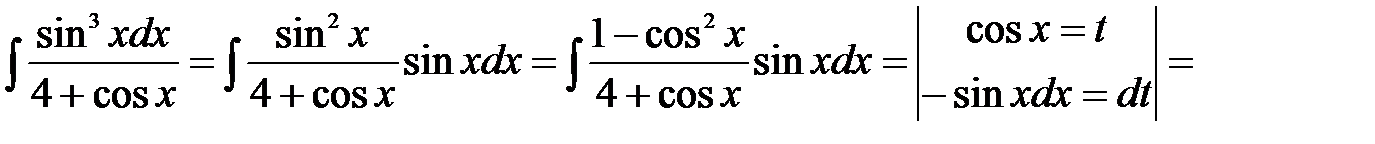
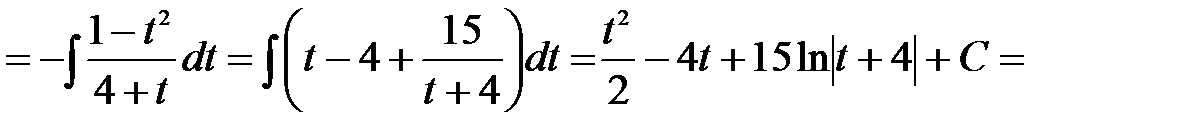
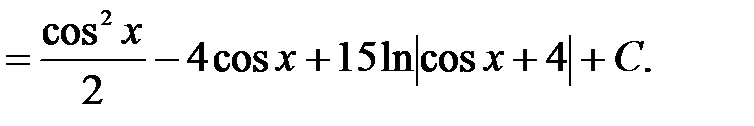
4) 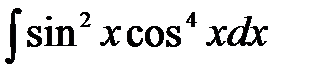 .
.
Решение: Используя формулы понижения степени, получим
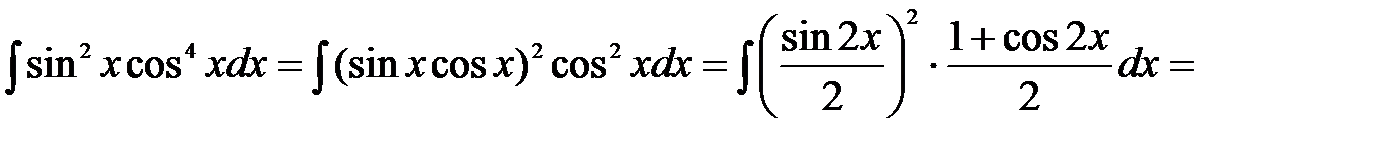
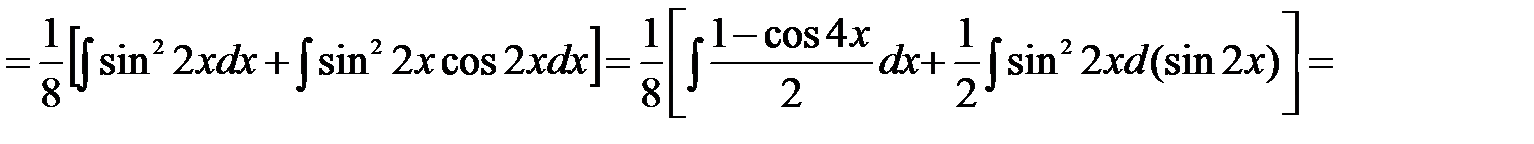
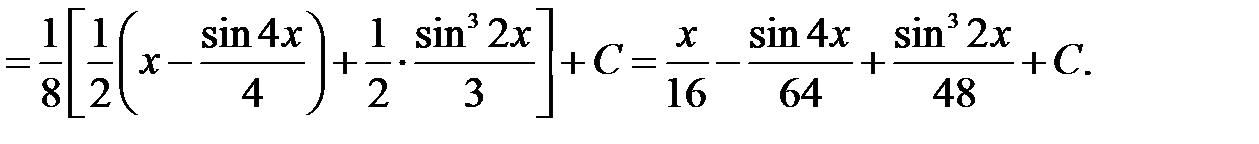
5) 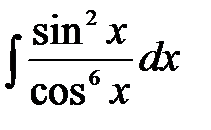 .
.
Решение: В данном случае применим подстановку 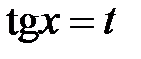 и формулу
и формулу 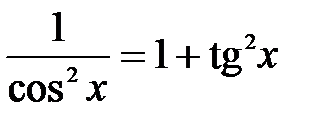 . Тогда
. Тогда
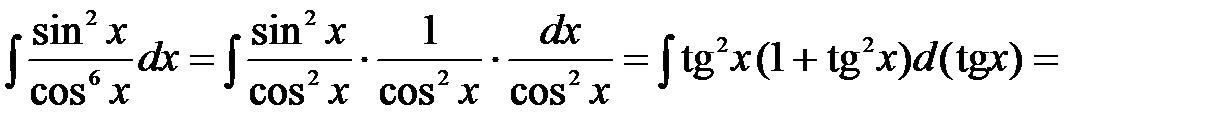
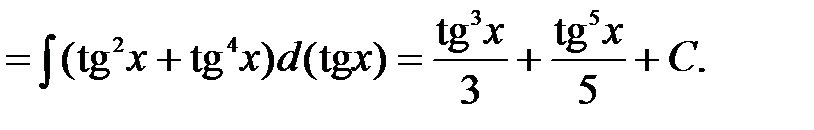
6) 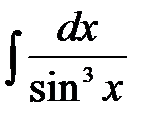 ,
,
Решение: Представим числитель по формуле 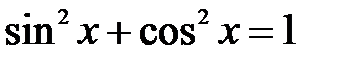 и разделим почленно числитель на знаменатель, получим
и разделим почленно числитель на знаменатель, получим
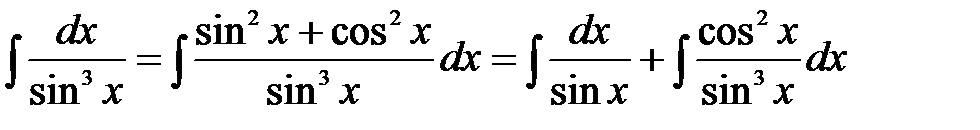 .
.
Для нахождения первого интеграла воспользуемся универсальной тригонометрической подстановкой 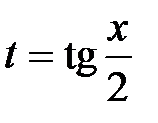 , имеем
, имеем
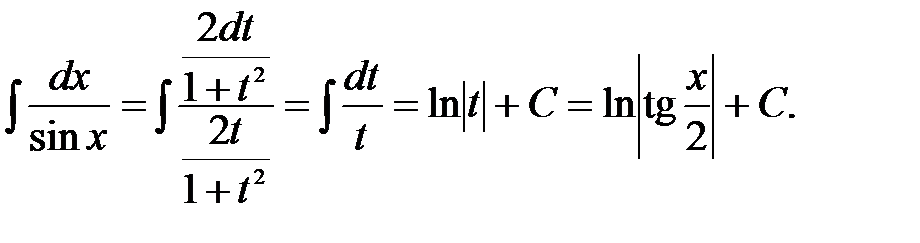
Для нахождения второго интеграла воспользуемся методом интегрирования по частям. Полагая  ,
, 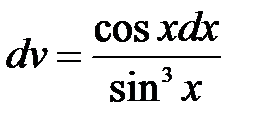 , имеем
, имеем
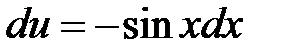 ,
, 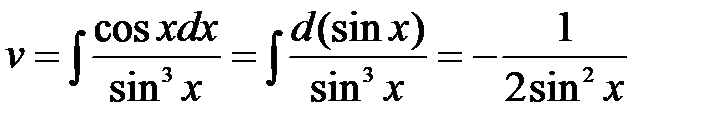 .
.
Следовательно,
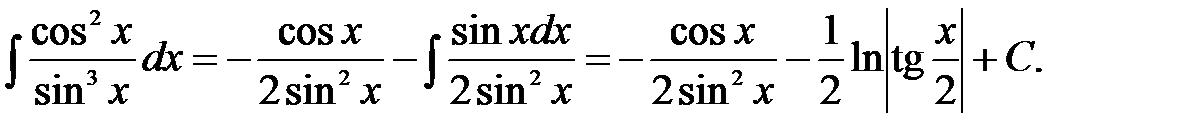
Итак, находим искомый интеграл
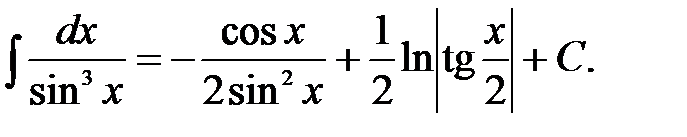
7) 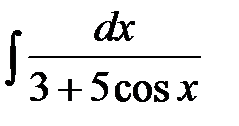 ,
,
Решение: Воспользуемся универсальной тригонометрической подстановкой 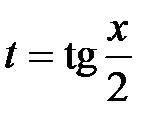 . Имеем
. Имеем
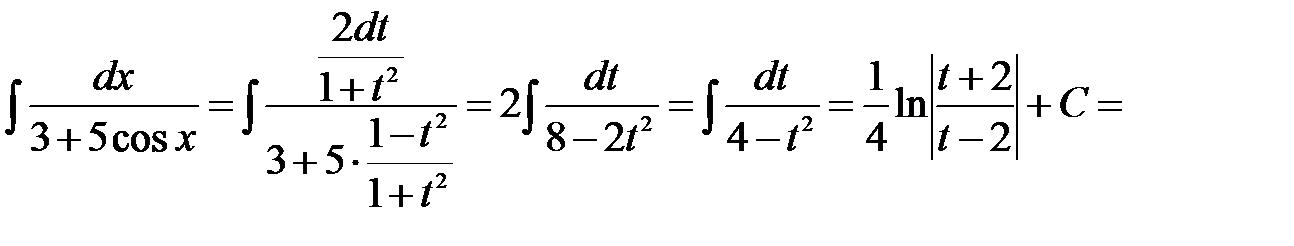
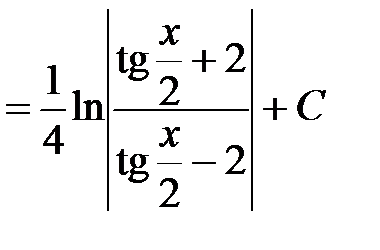 .
.
8) 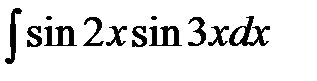 .
.
Решение: Воспользуемся тригонометрической формулой преобразования произведения в сумму, получим
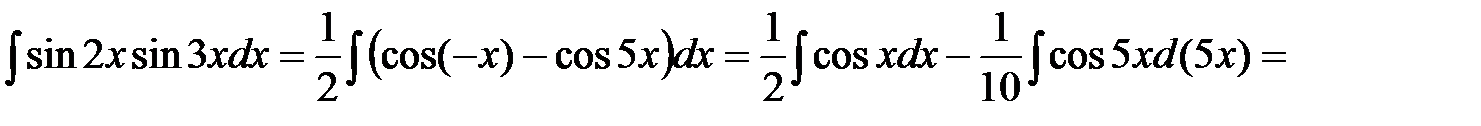
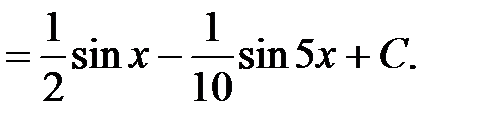
 2018-01-08
2018-01-08 791
791








