Понятие сложной и обратной функций. Примеры

1. Понятие о сложной функции

Пусть даны две функции z = f(y) и у = g(x). Сложной функцией (или композицией функций f и g) называется функция z = h(x), значения которой вычисляются по правилу h(x) = f(g(x)) (т. е. сначала вычисляется g(x), при этом получается некоторое число у, а затем вычисляется значение в точке у).

Пример. Функцию 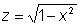можно рассматривать как композицию функци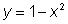й и .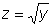

Для записи композиции функций употребляется значок 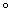. Например, запись 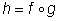означает, что функция h получена как композиция функций f и g (сначала применяется g, а затем f), т. е. .

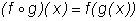Чтобы можно было вычислить сложную функциюh = f(g(x)), надо, чтобы число g(x), т. е. значение функции g, попадало в область определения функции f.

Пример.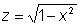

Вычисляя значения функции 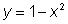, необходимо брать только те числа х, для которых 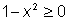, т. е. те, для которых число 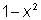попадает в область определения функции .

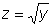2. Взаимно обратные функции

Пусть дана функция у = f(x). Она имеет обратную, если из зависимости у = f(x) можно переменную х однозначно выразить через переменную у. Выразив х через у, мы получим равенство вида х = g(y). В этой записи g обозначает функцию, обратную к f.

Если функция g является обратной для функции f, то и функция является обратной для функции g.

Пару функций f и g называют взаимно обратными функциями.