Свойства функции arcsin
§  (функция является нечётной).
(функция является нечётной).
§ 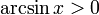 при
при  .
.
§  при x = 0.
при x = 0.
§  при
при 
§ 
§ 
§ 
Арккосинусом числа m называется такое значение угла x, для которого:

Свойства функции arccos
§  (функция центрально-симметрична относительно точки
(функция центрально-симметрична относительно точки 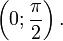
§  при
при 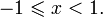
§  при
при 
§ 
§ 
§ 
§ 
§ 
 Арктангенсом числа m называется такое значение угла α, для которого:
Арктангенсом числа m называется такое значение угла α, для которого:
Свойства функции arctg
§ 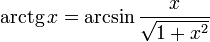
§ 
Арккотангенсом числа m называется такое значение угла x, для которого:

Свойства функции arcctg
§  (график функции центрально-симметричен относительно точки
(график функции центрально-симметричен относительно точки 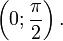
§  при любых x.
при любых x.
§ 
19.

20.

21.

22. числовая функция — это функция, области определения и значений которой являются подмножествами числовых множеств — как правило, множества вещественных чисел  или множества комплексных чисел
или множества комплексных чисел  .
.
Обычно функция задаётся с помощью формулы, в которую входят переменные, операции и элементарные функции. Возможно, кусочное задание, то есть различное для различных значений аргумента.
Примеры:
§  ;
;
§  ;
;
§  ;
;
§ 
Табличный способ
Функцию можно задать, перечислив все её возможные аргументы и значения для них. После этого, если это необходимо, функцию можно доопределить для аргументов, которых нет в таблице, путём интерполяции или экстраполяции. Примерами могут служить программа передач, расписание поездов или таблица значений булевой функции:
 |  |  |
Графический способ
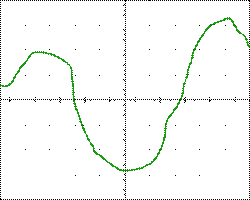

Осциллограмма задаёт значение некоторой функции графически.
Функцию можно задать графически, отобразив множество точек её графика на плоскости. Это может быть приблизительный набросок, как должна выглядеть функция, или показания, снятые с прибора, например, с осциллографа. Этот способ задания может страдать от недостаткаточности, однако в некоторых случаях другие способы задания вообще не могут быть применены. Кроме того, такой способ задания один из самых презентативных, удобных для восприятия и качественного эвристического анализа функции.
Рекурсивный способ
Функция может быть задана рекурсивно, то есть через саму себя. В этом случае одни значения функции определяются через другие её значения.
Примеры:
§ факториал;
§ числа Фибоначчи;
§ функция Аккермана.
Словесный способ
Функцию можно описать словами на естественном языке каким-либо однозначным способом, например, описав её входные и выходные значения, или алгоритм, с помощью которого функция задаёт соответствия между этими значениями. Наряду с графическим способом, иногда это единственный способ описать функцию, хотя естественные языки и не стольдетерминированы, как формальные.
Примеры:
§ функция, возвращающая цифру в записи числа пи по её номеру;
§ функция, возвращающая число атомов во вселенной в определённый момент времени;
§ функция, принимающая в качестве аргумента человека, и возвращающая число людей, которое родится на свет после его рождения.
23. График функции — множество точек, у которых абсциссы являются допустимыми значениями аргумента x, а ординаты — соответствующими значениями функции y.
Обычно рассматриваются графики вещественных скалярных функций одного вещественного переменного  , которые являются множеством точек плоскости
, которые являются множеством точек плоскости  .
.
В общем случае, график функции (оператора)  есть множество
есть множество
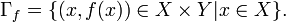
| Общий вид функции | Преобразования |
| y = f (x - b) | Параллельный перенос графика вдоль оси абсцисс на | b | единиц
|
| y = f (x + b) |
|
| y = f (x) + m | Параллельный перенос графика вдоль оси ординат на | m | единиц
|
| Отражение графика | |
| y = f (- x) | Симметричное отражение графика относительно оси ординат. |
| y = - f (x) | Симметричное отражение графика относительно оси абсцисс. |
| Сжатие и растяжение графика | |
| y = f (kx) |
|
| y = kf (x) |
|
| Преобразования графика с модулем | |
| y = | f (x) | |
|
| y = f (| x |) |
|

24.
1) Монотонность функции.
Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
2) Четность (нечетность) функции.
Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.
Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = - f(x). График нечетной функции симметричен относительно начала координат.
3) Ограниченная и неограниченная функции.
Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x. Если такого числа не существует, то функция - неограниченная.
4) Периодическость функции.
Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).
5) Точки, в которых достигается максимум или минимум функции, называются точками экстремума.
В точке экстремума происходит смена характера монотонности функции. Так, слева от точки экстремума функция может возрастать, а справа – убывать. Согласно определению, точка экстремума должна быть внутренней точкой области определения.
Если для любого  (x ≠ a) выполняется неравенство f (x) ≤ f (a)
(x ≠ a) выполняется неравенство f (x) ≤ f (a) 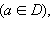 то точка a называется точкой наибольшего значения функции на множестве D:
то точка a называется точкой наибольшего значения функции на множестве D:

Если для любого  (x ≠ b) выполняется неравенство f (x) > f (b)
(x ≠ b) выполняется неравенство f (x) > f (b)  то точка b называется точкой наименьшего значения функции на множестве D.
то точка b называется точкой наименьшего значения функции на множестве D.
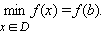
Точка наибольшего или наименьшего значения может быть экстремумом функции, но не обязательно им является.
25.
Схема исследования функции
1. Область определения
2. Исследование функции на четность, нечетность и периодичность
Если область определения функции симметрична относительно нуля и для любого x из области определения выполнено равенство  , то
, то  – четная функция; если область определения функции симметрична относительно нуля и для любого x из области определения выполнено равенство
– четная функция; если область определения функции симметрична относительно нуля и для любого x из области определения выполнено равенство  , то
, то  – нечетная функция; в противном случае,
– нечетная функция; в противном случае, 
 – общего вида. График четной функции симметричен относительно оси ординат, график нечетной функции симметричен относительно начала координат.
– общего вида. График четной функции симметричен относительно оси ординат, график нечетной функции симметричен относительно начала координат.
3. Нахождение точек пересечения графика функции с осями координат
Точки пересечения с осью ОХ:  , где
, где  – решение уравнения
– решение уравнения  .
.
Точки пересечения с осью ОY:  .
.
4. Нахождение промежутков знакопостоянства функции
Промежутки знакопостоянства функции – промежутки из области определения функции, где функция принимает положительные или отрицательные значения, т.е.  или
или  .
.
5. Нахождение производной функции, области определения производной, критических точек
Критические точки функции – внутренние точки области определения функции, в которых производная не существует или равна нулю.
6. Нахождение промежутков возрастания, убывания, точек экстремума и экстремумов
Критические точки функции разбивают область определения функции на промежутки. Для нахождения промежутков возрастания, убывания и точек экстремума нужно определить знак производной на каждом из полученных промежутков. Если производная функции положительна на некотором промежутке I, то функция возрастает на этом промежутке; если производная функции отрицательна на некотором промежутке I, то функция убывает на этом промежутке. Если при переходе через критическую точку производная меняет знак, то данная точка является точкой экстремума.
7. Нахождение промежутков выпуклости функции и точек перегиба
Для нахождения промежутков выпуклости используется вторая производная функции. Точки, в которых вторая производная равна нулю или не существует, разбивают область определения функции на промежутки. Если вторая производная на полученном промежутке положительна, то график функции имеет выпуклость вниз, если – отрицательна, то график функции имеет выпуклость вверх. Если при переходе через точку, в которой вторая производная равна нулю или не существует, вторая производная меняет знак, то данная точка является точкой перегиба.
8. Исследование поведения функции на бесконечности и в окрестности точек разрыва
Для исследования поведения функции в окрестности точки разрыва 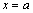 необходимо вычислить односторонние пределы:
необходимо вычислить односторонние пределы:  и
и 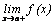 . Если хотя бы один из данных пределов равен бесконечности, то говорят, что прямая
. Если хотя бы один из данных пределов равен бесконечности, то говорят, что прямая 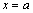 – вертикальная асимптота.
– вертикальная асимптота.
При исследовании поведения функции на бесконечности необходимо проверить, не имеет ли график функции наклонных асимптот при 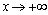 и
и  . Для этого нужно вычислить следующие пределы:
. Для этого нужно вычислить следующие пределы:  и
и 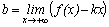 . Если оба предела существуют, то
. Если оба предела существуют, то  – уравнение наклонной асимптоты при
– уравнение наклонной асимптоты при  . Частный случай наклонной асимптоты при
. Частный случай наклонной асимптоты при  – горизонтальная асимптота. Аналогично ищется наклонная асимптота при
– горизонтальная асимптота. Аналогично ищется наклонная асимптота при  .
.
9. Построение графика (при необходимости нужно найти значения функции в дополнительных точках)
Пример 1. Построить график функции  с помощью производной первого порядка.
с помощью производной первого порядка.
Решение. 1. 
2.  и
и  . Следовательно, функция
. Следовательно, функция  общего вида.
общего вида.
3. Точки пересечения с осями координат:
ОХ: 
 ,
,
 . (-1; 0), (3; 0)
. (-1; 0), (3; 0)
OY:  ,
, 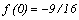 (0; -9/16)
(0; -9/16)
 4. Промежутки знакопостоянства:
4. Промежутки знакопостоянства:
 при
при 
5. 
Критические точки: 
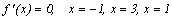

 6.
6.
 возрастает на промежутке
возрастает на промежутке 
 убывает на промежутке
убывает на промежутке 
Точки экстремума: 
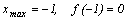 ;
; 
7. Асимптот нет
8. Дополнительные точки:  ,
, 
9.

26.
1)Линейная функция - это функция вида:
y = kx + b
здесь k и b являются действительными числами.
Линейная функция имеет следующие свойства:
1. Множество значений лнейной функции - вся числовая прямая;
2. Область определения функции y = kx + b - вся числовая прямая;
3. y = kx + b - это ни чётная, ни нечётная функция;
4. Если k > 0, то функция возрастает, а если k < 0, то линейная функция убывает.
График линейной функции есть прямая. Вот график линейной функции y = 2x + 1

| 2)Если k=0, то получаем постоянную функциюy=b, ее графиком является прямая, параллельная оси абсцисс и проходящая через точку (0;b) на оси ординат. В частности, графиком функции y=0 является ось абсцисс. | 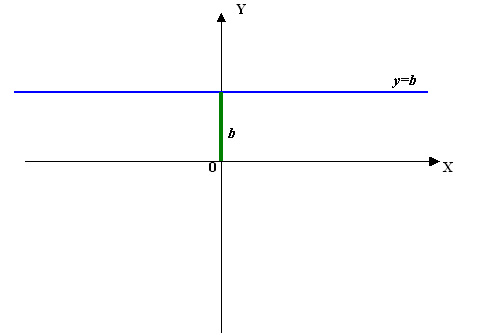 |
 2018-01-08
2018-01-08 1304
1304
 0 — график остаётся без изменений,
0 — график остаётся без изменений,