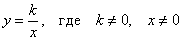
 | 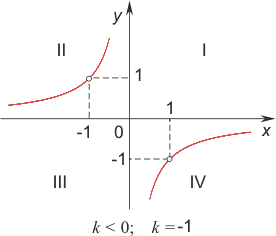 |
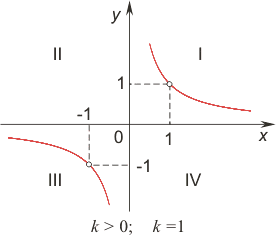
| График обратно пропорциональной зависимости — кривая (гипербола), состоящая из двух ветвей, симметричных относительно начала координат. k — коэффициент обратной пропорциональности, действительное число (k ≠0). k >0, функция убывающая, ветви гиперболы расположены в I и III координатных четвертях. k <0, функция возрастающая, ветви гиперболы расположены во II и IV координатных четвертях. Область определения есть множество всех чисел, отличных от нуля, т.е. (−∞; 0)∪(+∞;). Гипербола не имеет общих точек с осями координат, а лишь сколь угодно близко приближается к ним, т.к. х ≠0. |
27.
При a > 0, a 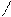 = 1, определена функция y=ax , отличная от постоянной. Эта функция называется показательной функцией с основанием a.
= 1, определена функция y=ax , отличная от постоянной. Эта функция называется показательной функцией с основанием a.
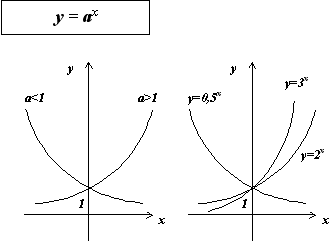
Основные свойства показательной функции y = a x при a > 1:
- Область определения функции - вся числовая прямая.
- Область значений функции - промежуток (0;+
 ).
). - Функция строго монотонно возрастает на всей числовой прямой, то есть, если x 1 < x 2, то ax 1 < ax 2.
- При x = 0 значение функции равно 1.
- Если x > 0, то a x > 1 и если x < 0, то 0 < a < 1.
|
|
|
Графики показательных функций с основанием 0 < a < 1 и a > 1 изображены на рисунке.
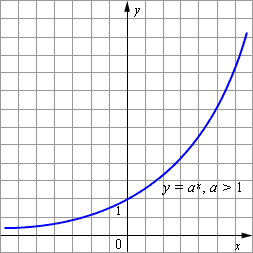 | 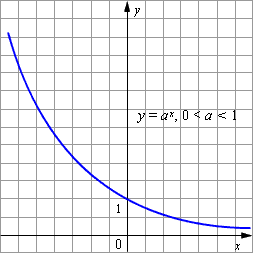 |
Основные свойства показательной функции y = a x при 0 < a < 1:
- Область определения функции - вся числовая прямая.
- Область значений функции - промежуток (0;+
 ).
). - Функция строго монотонно возрастает на всей числовой прямой, то есть, если x 1 < x 2, то ax 1 > ax 2.
- При x = 0 значение функции равно 1.
- Если x > 0, то 0 < a < 1 и если x < 0, то a x > 1.
К общим свойствам показательной функции как при 0 < a < 1, так и при a > 1 относятся:
- ax 1 ax 2 = ax 1+ x 2, для всех x 1и x 2.
- a − x =(ax)−1=1 ax для любого x.
-
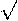 nax = axn для любого x и любого n
nax = axn для любого x и любого n 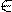 N
N  n
n 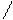 =1.
=1. - (ab) x = ax bx для любых a, b > 0; a,b
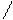 =1.
=1. - (ba) x = bxax для любых a, b > 0; a,b
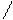 =1.
=1. - ax 1 = ax 2, то x 1= x 2.
28.
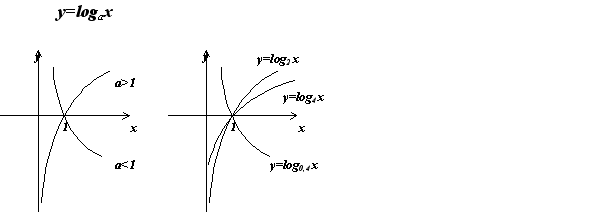
Функция y = loga х (где а > 0, а 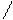 = 1) называется логарифмической.
= 1) называется логарифмической.
Построение графиков. График логарифмической функции log aх можно построить, воспользовавшись тем, что функция log aх обратна показательной функции y = ax. Поэтому достаточно построить график функции y = ax, а затем отобразить его симметртрично относительно прямой у = х.
Свойства функции у = logaх, a > 1:
- D(f) = (0; +
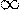 );
); - не является ни четной, ни нечетной;
- возрастает на (0; +
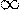 );
); - не ограничена сверху, не ограничена снизу;
- не имеет ни наибольшего, ни наименьшего значений;
- непрерывна;
- E(f) = (-
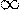 ;+
;+ 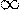 );
); - выпукла вверх;
- дифференцируема.
Свойства функции у = l ogaх, 0 < a < 1:
- D(f) = (0;+
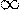 );
); - не является ни четной, ни нечетной;
- убывает на (0; +
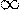 );
); - не ограничена сверху, не ограничена снизу;
- нет ни наибольшего, ни наименьшего значений;
- непрерывна;
- E(f) = (-;
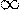 +
+ 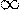 );
); - выпукла вниз;
- дифференцируема.
Свойства функции у = ln х:
- D(f) = (0; +
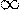 );
); - не является ни четной, ни нечетной;
- возрастает на {0; +
 );
); - не ограничена сверху, не ограничена снизу;
- не имеет ни наибольшего, ни наименьшего значений;
- непрерывна;
- E(f) = (-
 ;+
;+  );
); - выпукла вверх;
- дифференцируема.
|
|
|
29. Степенной функцией с вещественным показателем a называется функция y = x n , x > 0.
Заметим, что для натуральных n степенная функция определена на всей числовой оси.
Для произвольных вещественных n это невозможно, поэтому степенная функция с вещественным показателем определена только для положительных x.
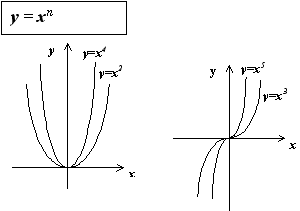
К основным свойствам степенной функции y = x a при a > 0 относятся:
- Область определения функции - промежуток (0; +
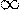 ).
). - Область значений функции - промежуток (0; +
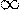 ).
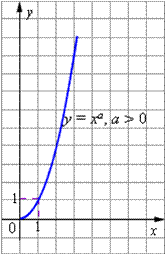
). - Для любых a график функции проходит через точку (1; 1).
- Функция строго монотонно возрастает в области определения функции, то есть, если x1 < x2 то ar1 < ar2.
- График степенной функции при a > 0 изображен на рисунке.
 | 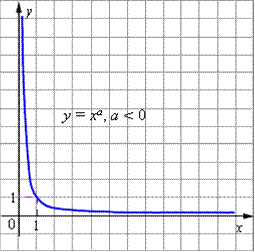 |
К основным свойствам степенной функции y = x a при a < 0 относятся:
- Область определения функции - промежуток (0; +
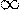 ).
). - Область значений функции - промежуток (0; +
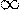 ).
). - Для любых a график функции проходит через точку (1; 1).
- Функция строго монотонно возрастает в области определения функции, то есть, если x1 < x2 то ar1 > ar2.
- График степенной функции при a < 0 изображен на рисунке.
Справедливы следующие свойства степенной функции:
- xa1xa2 = xa1 + a2
- xa1: xa2 = xa1 - a2
- (xa1) a2 = xa1 a2
- xa1 > xa2, x > 1, a1 > a2
- xa1 < xa2, 0 < x < 1, a1 < a2
30.
Y = cos x
а) Область определения: D (cos x) = R.
б) Множество значений: E (cos x) = [ – 1, 1 ].
в) Четность, нечетность: функция четная.
г ) Периодичность: функция периодическая с основным периодом T = 2 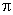 .
.
д) Нули функции: cos x = 0 при x = 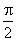 +
+ 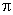 n, n
n, n 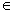 Z.
Z.
е) Промежутки знакопостоянства:
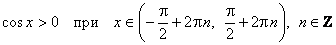 ;
;
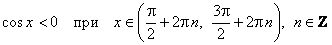 .
.
. ж) Промежутки монотонности:
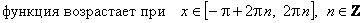 ;
;
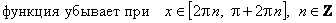 .
.
з) Экстремумы:
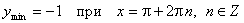 ;
; 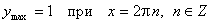 .
.
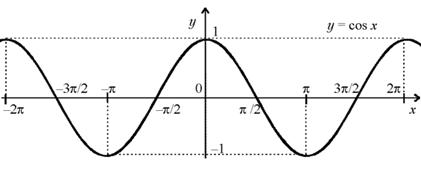
График функции y = cos x изображен на рисунке.
31.
Y=sin x
а) Область определения: D (sin x) = R.
б) Множество значений: E (sin x) = [ – 1, 1 ].
в) Четность, нечетность: функция нечетная.
г ) Периодичность: функция периодическая с основным периодом T = 2 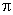 .
.
д) Нули функции: sin x = 0 при x = 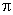 n, n
n, n 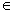 Z.
Z.
е) Промежутки знакопостоянства:
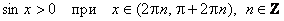 ;
; 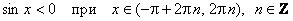 .
.
ж) Промежутки монотонности:
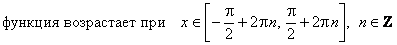 ;
;
 .
.
з) Экстремумы:
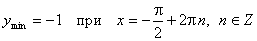 ;
; 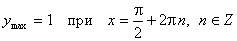 .
.
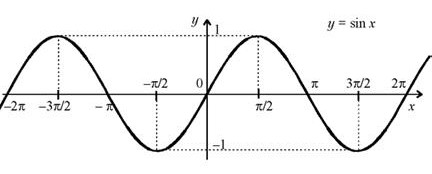
График функции y = sin x изображен на рисунке.
32.
Y=tg x
а) Область определения: D (tg x) = R \ { 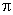 /2 +
/2 + 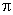 n (n
n (n 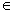 Z) }.
Z) }.
б) Множество значений: E (tg x) = R.
в) Четность, нечетность: функция нечетная.
г ) Периодичность: функция периодическая с основным периодом T = 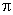 .
.
д) Нули функции: tg x = 0 при x = 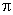 n, n
n, n 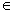 Z.
Z.
е) Промежутки знакопостоянства:
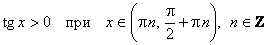 ;
; 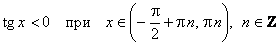 .
.
ж) Промежутки монотонности: функция возрастает на каждом интервале, целиком принадлежащем ее области определения.
з) Экстремумы: нет.
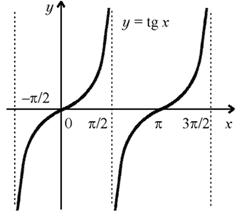
График функции y = tg x изображен на рисунке.
33.
Размещения.
Размещениями из 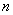 элементов по
элементов по 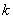 называются соединения, которые можно образовать из
называются соединения, которые можно образовать из 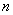 элементов, собирая в каждое соединение по
элементов, собирая в каждое соединение по 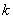 элементов, при этом соединения могут отличаться друг от друга как самими элементами, так и порядком их расположения.
элементов, при этом соединения могут отличаться друг от друга как самими элементами, так и порядком их расположения.
Например, из 3 элементов (a,b,c) по 2 можно образовать следующие размещения:
ab, ac, ba, bc, ca, cb.
Число всех возможных размещений, которые можно образовать из 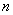 элементов по
элементов по 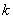 , обозначается символом
, обозначается символом 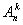 и вычисляется по формуле:
и вычисляется по формуле:
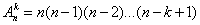 ,
,
(всего k множителей).
Пример: 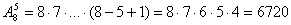
Перестановки.
Перестановками из n элементов называются соединения, каждое из которых содержит все n элементов, отличающихся поэтому друг от друга только порядком расположения элементов.
Например, из 3 элементов (a,b,c) можно образовать следующие перестановки:
abc, bac, cab, acb, bca, cba.
Число всех возможных перестановок, которые можно образовать из n элементов, обозначается символом 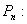
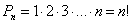
(Произведение n первых целых чисел обозначается символом “ n!” и читается “ n факториал”)
Пример: 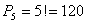
Сочетания.
Сочетаниями из n элементов по k называются соединения, которые можно образовать из n элементов, собирая в каждое соединение k элементов; при этом соединения отличаются друг от друга только самими элементами (различие порядка их расположения во внимание не принимается).
|
|
|
Например, из 3 элементов (a,b,c) по 2 можно образовать следующие сочетания:
ab, ac, bc.
Число всех возможных сочетаний, которые можно образовать из n элементов по k, обозначается символом 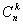 :
:
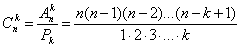
(В числителе и знаменателе по k множителей).
Пример: 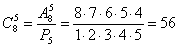
Полезные формулы:
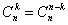
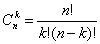
Например: 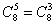
 2018-01-08
2018-01-08 3240
3240