1.3.1. Векторная форма записи КЗЛП и ее применение. Рассмотрим каноническую задачу линейного программирования

Обозначим через аj столбцы матрицы А и будем рассматривать их как векторы пространства Rm. Тогда каждому допустимому плану КЗЛП — n -мерному вектору х — соответствует неотрицательная линейная комбинация столбцов аj, равная столбцу bÎ Rm:

Такое представление ограничений КЗЛП обычно называют векторной формой записи.
Векторы аj, j Î l :n будем называть векторами требований задачи (D, f), а вектор b — вектором ограничений. Множество всех неотрицательных линейных комбинаций столбцов аj с геометрической точки зрения может быть представлено как многогранный выпуклый конус, натянутый на систему векторов аj в пространстве Rm (рис. 1.3).
Соответственно, вопрос о существовании допустимого плана задачи (D, f) равнозначен вопросу о принадлежности вектора b данному конусу, а компоненты хj некоторого допустимого плана х Î D являются не чем иным, как коэффициентами разложения вектора ограничений задачи b по векторам, требований аj.
Такое представление КЗЛП получило название второй геометрической интерпретации.
В дальнейшем без ограничения общности можем предполагать, что число уравнений, задающих множество D, меньше или равно числу переменных задачи (m ≤ n). Действительно, если это не так, то либо система уравнений Ах = b несовместна (и, значит, множество D пустое), либо содержит избыточные (линейно зависимые) уравнения.
Если некоторые т столбцов аj 1, аj 2,..., аjm матрицы A являются линейно независимыми, то они образуют базис в пространстве Rm, и их, вообще говоря, будет достаточно для представления вектора b в виде линейной комбинации указанных столбцов. Это означает, что остальные столбцы войдут в данное разложение с нулевыми коэффициентами. Если к тому же коэффициенты линейной комбинации окажутся неотрицательными, то мы получаем так называемый базисный допустимый план х, у которого не более m компонентов отличны от нуля. Сформулируем определение базисного плана более строго, так как это одно из фундаментальных понятий теории линейного пpогpаммиpования.

F F Пусть задана некоторая каноническая ЗЛП (D,f), А —матрица системы ограничений задачи, и β= {аj1, аj2,..., аjm} —линейно независимая система столбцов матрицы А, образующая базис Rm. Обозначим множество номеров столбцов, входящих в систему b, через N (β) = {j1, j2,..., jm}. План х называется базисным планом задачи (D,f), если его компоненты, соответствующие базисным столбцам и называемые базисными компонентами, больше или равны нулю (хj ≥ 0, j Î N (β)}, а все остальные компоненты (небазисные) — равны нулю (xj = 0, j Ï N (β)).
F F Базисный план х называется невырожденным, если все его базисные компоненты строго
положительны, и вырожденным в противном случае.
1.3.2. Свойства базисных планов. Следующая теорема трактует понятие базисного плана в терминах первой геометрической интерпретации ЗЛП.
| Теорема 1.3. Каждый допустимый базисный план является угловой точкой множества допустимых планов D. |
Доказательство.
Ради простоты положим, что базисными векторами являются первые m столбцов матрицы A, т. е. β={ a l, a 2,..., am }. Тогда утверждение теоремы 1.3 может быть переформулировано следующим образом:
Если существует такой n-мерный вектор

что x 1 a 1 + х 2 а 2 +...+ xk ak = b, то х есть угловая точка множества D.
Проведем доказательство от противного, т. е. предположим, что рассматриваемый базисный план х не является угловой точкой множества D. Тогда ее можно представить в виде выпуклой комбинации некоторых двух различных допустимых планов х 1 и х 2:
x = λ x 1+(1-λ) x 2, 0<λ<1.
В координатной форме последнее утверждение означает

Поскольку последние (n - k) компоненты вектора х по предположению равны 0, а числа хj 1, xj 2 ≥ 0 и λ, (1 -λ)>0, то эти же компоненты в векторах x 1 и х 2 также равны 0. Поэтому, с учетом допустимости планов х 1 и х 2, можно утверждать, что

Вычитая из (1.15) (1.16), получим
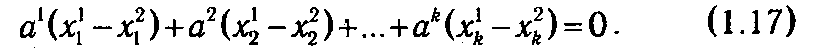
Так как векторы а 1, а 2,..., аk — линейно независимы, то коэффициенты х 11 – х 21 =0,..., х1k –х2k =0, из чего следует, что x 1 = х 2. Это противоречит предположению, что х 1 и х 2 являются различными угловыми точками множества D. Следовательно, х не может быть представлен в виде выпуклой комбинации двух точек D и по определению является угловой точкой данного множества. A
Интересно отметить, что справедливо и обратное утверждение, которое приведем без доказательства:
Если х — угловая точка множества D, то она является допустимым базисным планом задачи (D, f).
В завершение параграфа необходимо отметить практическое значение установленной связи между угловыми точками и допустимыми базисными решениями: она позволяет формализовать (и тем самым существенно упростить) процесс перехода от одной угловой точки к другой.
СИМПЛЕКС-МЕТОД
1.4.1. Основные этапы симплекс-метода. Исходя из свойств линейных экстремальных задач, рассмотренных в предыдущих параграфах, можно заключить, что на принципиальном уровне поиск их решений сводится к последовательному перебору угловых точек множества допустимых планов или, что то же самое, перебору соответствующих допустимых базисных планов. Следует подчеркнуть, что такой перебор для реальных многомерных задач возможен только в теоретическом плане и на практике неосуществим (или крайне неэффективен) даже при условии использования мощной вычислительной техники. Средством решения данной проблемы явились прикладные оптимизационные методы, основанные на последовательном, целенаправленном переборе базисных планов ЗЛП.
Классическим методом решения ЗЛП стал симплекс-метод, получивший также в литературе название метода последовательного улучшения плана, разработанный в 1947г. американским математиком Джорджем Данцигом.
Идея такого перехода от одного базисного плана к другому, при котором происходит «улучшение» значения целевой функции, может быть продемонстрирована для случая m = 2 с помощью рис. 1.4. Если вектор ограничений b принадлежит конусу, натянутому на некоторые два базисных вектора условий {аj1,аj2}, то существует такой базисный план х с базисными компонентами хj1, хj2, что b= хj1aj1 + хj2aj2. Разумеется, таких планов может быть несколько в зависимости от выбора системы базисных векторов. Чтобы различать их по соответствующей величине целевой функции f(x)=cj 1 xj 1 + сj 2 хj 2, вводятся так называемые расширенные векторы условий и ограничений. В общем случае расширенный столбец условий āj получается соединением коэффициента целевой функции сj и столбца аj:
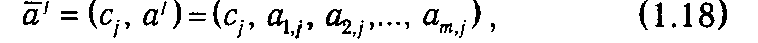
расширенный вектор ограничений определим как

В дальнейшем для удобства нумерации элементов будем считать, что добавляемый коэффициент целевой функции сj является нулевым элементом j -го расширенного столбца условий, т. е. ā0,j = сj. При изображении расширенных векторов нулевая координата откладывается вдоль вертикальной оси — оси аппликат.
Рассмотрим также вектор

=
Геометрически определение вектора b означает, что он принадлежит конусу, натянутому на расширенные векторы, а вектор служит его проекцией. Нулевая координата вектора b имеет вид:

т. е. равна значению целевой функции для выбранного базисного плана.
Из геометрической иллюстрации следует, что для решения задачи мы должны среди векторов аj выбрать такой набор {аj1,аj2}, чтобы, прямая, проведенная через конец вектора параллельно оси аппликат, пересекала конус, натянутый на систему соответствующих расширенных столбцов { āj1, āj2}, в «наивысшей» точке.
На рис. 1.4 выделен конус, натянутый на систему расширенных столбцов ā2 и ā3, отвечающих текущему допустимому базису. Нетрудно заметить, что данный базис не является оптимальным, например, для базиса { а3, а4 } точка пересечения соответствующего конуса и прямой будет находиться выше. Можно, наоборот, указать базис с «худшим» значением целевой функции: { а1 а2 }. Наконец, рассматриваемая геометрическая интерпретация КЗЛП иллюстрирует и общую идею критерия, который используется в симплекс-методе для определения оптимальности (или неоптимальности) текущего плана: если существуют векторы-столбцы, лежащие выше плоскости, проходящей через векторы текущего базиса, то он не является оптимальным и может быть «улучшен».

С вычислительной точки зрения критерий оптимальности в симплекс-методе реализуется через нахождение специальных оценок для небазисных векторов-столбцов, относительно текущего базиса.
Для удобства дальнейшего изложения введем некоторые обозначения. Учитывая то, что симплекс-метод представляет собой некоторый итеративный вычислительный процесс, то через q будем обозначать номер очередной (текущей) итерации. Соответственно, набор базисных столбцов, получаемых на q -й итерации, будет обозначаться как β ( q ):

Для того чтобы было легче отличить номер итерации от номеров компонентов матриц и векторов, он заключен в круглые скобки. Номера столбцов, входящих в базис, обозначим через N (β(q)), а именно

При этом Nr (β(q)) = jr — номер столбца, занимающего r -ю позицию в базисе. Тогда текущий базисный план х имеет вид:

Обозначим через Δ(ß(q)) матрицу, составленную из столбцов {аj1, аj2,..., аjm}, образующих базис, через Δ(ß(q)) матрицу, образованную из соответствующих расширенных столбцов и дополненную слева столбцом специального вида:

а через ∆-1(β(q)) и ∆-1(β(q)) — матрицы, обратные по отношению к ним. Также представляется удобным ввести отдельные обозначения для элементов матрицы ∆-1(β(q)):
δ i (β(q)) — i -я строка матрицы ∆ˉ-1(β(q)), (i Î 0: m);
δ ij (β(q)) — элемент матрицы ∆-1(β(q)), находящийся в i -й строке j -го столбца (i Î 0: m, j Î 0: m).
Расширенный вектор ограничений b представляется в виде линейной комбинации расширенных векторов условий с коэффициентами, равными базисным компонентам текущего базисного плана:

Если интерпретировать компоненты векторов а j и b как координаты в ортогональном базисе, то их столбцы координат относительно произвольного базиса (β(q)), дополненного единичным вектором (-1,0,..., 0), направленным противоположно оси аппликат примут вид:

а для расширенной матрицы задачи в целом можно записать
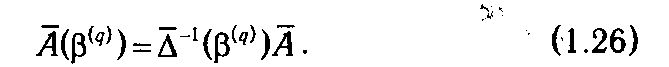
Нулевая строка данной матрицы a 0(β( q )) содержит координаты расширенных векторов условий по оси аппликат. Согласно построению, элементы данной строки имеют следующие знаки:
Ø Ø a 0,j (β( q )) < 0 — для расширенных векторов условий, расположенных выше плоскости, натянутой на систему расширенных базисных векторов;
Ø Ø a 0,j (β( q )) > 0 — для расширенных векторов условий, расположенных ниже плоскости, натянутой на систему расширенных базисных векторов;
Ø Ø a 0,j (β( q )) = 0 — для расширенных базисных векторов.
Подводя итог сказанному, сформулируем критерий оптимальности допустимого базисного плана в симплекс-методе:
F план является оптимальным, если для всех j Î1: n a 0,j (β( q )) ≥ 0, и неоптимальным в противном
случае, т. е. если существует такое l Î l: n, что a 0 l (β( q )) < 0.
Значения a 0,j (β( q ))также называют оценками столбцов матрицы А относительно текущего базиса, или симплекс-разностями.
В случае неоптимальности текущего базиса в алгоритме симплекс-метода осуществляется переход к следующему базису. Это делается за счет вывода одного столбца из базиса и ввода другого. Для обеспечения улучшения значения целевой функции в базис должен быть введен вектор-столбец, имеющий отрицательную оценку. Если таких столбцов несколько, то для ввода рекомендуется выбирать столбец, имеющий максимальную по модулю оценку. Отметим, что данное правило носит относительный характер и не гарантирует наилучшего выбора вводимого столбца. Одновременно на этой стадии требуется принять решение о том, какой столбец следует вывести из базиса. Сделать это нужно таким образом, чтобы вновь формируемый базис оказался допустимым. Данное требование может быть легко проиллюстрировано для случая m = 2. Например, на рис. 1.3 векторы { а 2, а 3} образуют допустимый базис, а векторы { а 3, a 4} —недопустимый, т. к. разложение b по а 3 и а 4 содержит один отрицательный компонент плана, что противоречит условиям КЗЛП.
Можно доказать, что допустимость базиса, к которому осуществляется переход, обеспечивается следующим правилом вывода столбца из текущего базиса:
F для столбца l, претендующего на ввод в базис, и вектора ограничений b рассматриваются
отношения

и определяется такая строка r, что

Полученный индекс r определяет номер столбца в N (β( q )), выводимого из базиса, а именно, N (β( q )).
Таким образом, если базис на q -й итерации включал столбцы с номерами

то базис на итерации q + 1 будет состоять из столбцов с номерами:

Отдельно следует обсудить тот случай, когда столбец al (β( q )), претендующий на ввод в базис, не содержит положительных компонентов al (β( q )) ≤ 0). Это означает, что целевая функция в задаче не ограничена на множестве допустимых значений, т. е. может достигать сколь угодно большого значения. Последнее, очевидно, означает завершение процесса вычислений ввиду отсутствия оптимального плана. Геометрически ситуация, когда a l (β( q )) ≤ 0, соответствует тому, что ось ординат оказывается внутри конуса, натянутого на систему расширенных столбцов аj, а значит, прямая, проведенная через конец вектора b параллельно оси аппликат, однажды «войдя» в этот конус, более никогда из него «не выходит».
Вообще говоря, после перехода от базиса β( q ) к базису β( q +1) мы можем заново сформировать матрицы ∆ (β( q+ 1)), Δ-1 (β( q +1)) и, вычислив А (β( q +1)) = Δ-1 (β( q +1)) A, делать выводы о его оптимальности. Однако, учитывая, что β( q +1) отличается от β( q ) всего лишь одним столбцом, с точки зрения техники вычислений представляется рациональным непосредственно переходить от A (β( q )) и b (β( q )) к A (β( q +1)) и b (β( q +1)). Дело в том, что у матриц типа A (β(q)) столбцы, соответствующие базисным векторам, состоят из нулей, за исключением одного элемента, равного единице. Позиция этого ненулевого элемента определяется порядковым номером базисного столбца в N (β( q )). Поэтому для получения матрицы A (β( q +1)) достаточно с помощью линейных операций над строками матрицы A (β( q )) привести ее столбец, соответствующий вводимому в базис вектору, к «базисному» виду.
Для это применяется преобразование Жордана—Гаусса (так называемый метод полного исключения). В данном случае оно состоит в том, что мы должны «заработать» единицу на месте элемента ar,l (β( q )) (он обычно называется ведущим)* и нули на месте остальных элементов столбца al (β( q )). Первое достигается посредством деления r -й строки на ведущий элемент, второе — путем прибавления вновь полученной r -й строки, умноженной на подходящий коэффициент, к остальным строкам матрицы A (β( q )).
* Напомним, что l — номер столбца, вводимого в базис, а r — номер строки в симплекс-таблице, определяющей номер столбца, выводимого из базиса.
Формально результат выполнения данного преобразования над элементами A (β( q )) и b (β( q )) может быть выражен в следующем виде
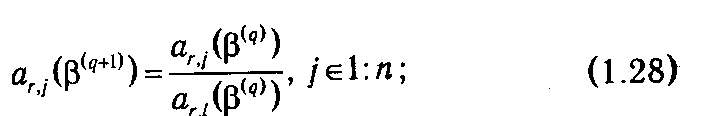

Следует особо отметить смысл элементов вектора b (β( q )). Его нулевой компонент b 0(β( q )) в соответствии с построением содержит значение целевой функции, достигаемое ею на текущем плане

а остальные элементы — ненулевые компоненты этого плана:

Название метода произошло от понятия симплекса. Напомним, что m-симплексом называют выпуклый многогранник, аффинная оболочка* которого есть аффинное множество размерности m. В данном случае можно считать, что система расширенных базисных столбцов { аj 1, аj 2,..., аjm }, рассматриваемых как точки в Rm +1, порождает (m -1)-мерный симплекс в пространстве Rm +1.
* Аффинной оболочкой множества называют наименьшее аффинное множество, в котором содержится данное множество.
В заключение настоящего пункта обобщим изложенные вопросы и приведем схему алгоритма симплекс-метода для решения задачи максимизации. Она включает однократно выполняемый 0-этап и повторяемый конечное число раз I-этап (стандартную итерацию).
0-этап. Нахождение допустимого базисного плана (см. п. 1.4.5). Результатом 0-этапа является допустимый базисный план х (β(1)), а также соответствующие ему матрица A (β(1)) и вектор b (β(1)), которые будут использованы на первой итерации. Полагаем номер текущей итерации q равным 1 и переходим к I-этапу.
I-этап. Стандартная итерация алгоритма — выполняется для очередного базисного плана x (β( q )).
1°. Проверка оптимальности текущего базисного плана: осуществляется просмотр строки оценок а 0(β(q)). Возможны два варианта:
1′. a 0(β( q ))≥0 — план, соответствующий текущему базису задачи, оптимален. Вычислительный процесс закончен. Согласно формулам (1.33) и (1.32) выписываются оптимальный план задачи х * = x (β( q )) и значение целевой функции f (x *) = f (x (β( q ))).
1″. В строке оценок а 0(β( q )) существует по меньшей мере один элемент а 0,j (β( q ))<0, т. е. имеющий отрицательную оценку. Следовательно, план x (β( q )) — неоптимален. Выбирается столбец с номером l, имеющий минимальную (максимальную по абсолютной величине) отрицательную оценку

Он называется ведущим и должен быть введен в очередной базис. Переходим к пункту 2° алгоритма.
2°. Определение столбца, выводимого из базиса. Рассматривается ведущий столбец аl (β( q )) Возможны два варианта:
2'. Для всех i Î1: m аi,l (β( q ))≤0. Делается вывод о неограниченности целевой функции и завершается вычислительный процесс.
2". Существует по крайней мере одна строка с номером i Î1: m, для которой аi,l (β( q ))>0. Согласно правилу (1.27) определяются место r и номер Nr (β(q)) = jr для столбца, выводимого из базиса. Переходим к пункту 3° алгоритма.
3°. Пересчет элементов матрицы А и столбца b относительно нового базиса. В соответствии с формулами (1.28)-(1.31) осуществляем расчет элементов матрицы задачи А и вектора ограничений b относительно базиса β( q+ 1), который получается после введения в базис β( q ) столбца аl и выводом из него столбца аr. Полагаем номер текущей итерации q: = q +l и переходим к первому пункту алгоритма.

Рис.1.5
1.4.2. Табличная реализация симплекс-метода. С точки зрения обеспечения рациональности и наглядности вычислительного процесса выполнение алгоритма симплекс-метода удобно оформлять в виде последовательности таблиц. В различных источниках приводятся разные модификации симплекс-таблиц, отличающиеся друг от друга расположением отдельных элементов. Однако это не должно вызывать смущения у читателя, так как все они базируются на одних и тех же принципах. Остановимся на структуре таблицы, показанной на рис. 1.5.*
* Настоящая структура симплекс-таблиц строится на идеях и принципах их организации, предложенных в [1].
Симплекс-таблица Т( q ), изображенная на рис. 1.5, соответствует допустимому базису КЗЛП β( q )), получаемому на q -й итерации. Столбец N (β( q )) содержит номера базисных столбцов (в той последовательности, в которой они входят в базис), столбец b (β( q )) —компоненты вектора ограничений относительно текущего базиса β( q ), A (β( q )) — компоненты матрицы задачи относительно текущего базиса β( q ). Наконец, в строке а 0(β( q )) находятся текущие оценки столбцов, а ячейка b 0(β( q )) содержит значение целевой функции, достигаемое для текущего плана.
Безусловно, следует добавить, что табличная модификация симплекс-метода имеет важное практическое значение не столько как удобная форма организации ручного счета, сколько как основа для реализации данного алгоритма в рамках программного обеспечения ЭВМ.
1.4.3. Пример решения ЗЛП симплекс-методом. Рассмотрим на конкретном примере процесс решения КЗЛП табличным симплекс-методом. Пусть дана каноническая задача ЛП:

Как видно, столбцы матрицы с номерами {5, 2, 3} являются линейно независимыми. И можно получить разложение по данным столбцам вектора ограничений с положительными коэффициентами. Последнее означает, что столбцы {5, 2, 3} образуют допустимый базис, с которого можно начать решение задачи. Из столбцов, входящих в базис, с учетом нулевых элементов формируется матрица Δ(β(1)) и обратная по отношению к ней Δ-1(β(1)):

Используя их, по формуле (1.26) получаем


| -84 | -88 | |||||
| 1/3 | 1/3 | |||||
| = | ; | |||||
| -2/3 | -4/3 |

Используя полученные значения A (β(1)) и b (β(1)), заполняем симплекс-таблицу T (1), соответствующую первой итерации (q =1).

Поскольку строка оценок a 0(β(1)) в первом и четвертом столбцах содержит отрицательные элементы (a 0,1(β(1)) = -84, a 0,4(β(1)) = -88), план х (β(1)) = (0,14,17/3,0,4) не является оптимальным, и значение целевой функции f (x (β(1))) = -226 может быть улучшено. Следуя рекомендации п.1˝ алгоритма симплекс-метода, полагаем номер вводимого в очередной базис столбца l = 4 (т.к. |-88| > |-84|). Рассматриваем ведущий столбец (выделен пунктирной рамкой)

Он содержит два положительных элемента. Применяя рекомендацию п. 2" алгоритма, получаем λ1= 4/(1/3) =12, λ2=14/3, и, стало быть r = 2. Следовательно, столбец с номером N 2(β(1)) = 2 должен быть выведен из базиса. Таким образом, получаем очередной допустимый базис задачи N (β(2)) = {5, 4, 3}. Элемент a 2,3(β(1)) является ведущим (обведен кружком). Применив формулы (1.28)-(1.31), переходим к симплекс-таблице, соответствующей второй итерации T (2), и полагаем индекс текущей итерации q = 2.

В ходе выполнения второй итерации опять-таки определяются вводимый столбец а 1, выводимый а 4 и ведущий элемент a 2,1(β(2)). Перейдя к итерации q = 3, имеем таблицу T (3).

Как видно из T (3), строка оценок содержит только неотрицательные значения, поэтому достигнутый базис N (β(3)) = {5, 1, 3} является оптимальным. В итоге мы получаем, что вектор х * = (7, 0, 31/3, 0, 5/3) является оптимальным планом (точкой максимума) задачи (1.34)-(1.35), максимальное значение целевой функции равно f * = f (х *)=362, а решение КЗЛП имеет вид ((7, 0, 31/3, 0, 5/3); 362).
1.4.4. Сходимость симплекс-метода. Вырожденность в задачах ЛП. Важнейшим свойством любого вычислительного, алгоритма является сходимость, т. е. возможность получения в ходе его применения искомых результатов (с заданной точностью) за конечное число шагов (итераций).
Легко заметить, что проблемы со сходимостью симплекс-метода потенциально могут возникнуть на этапе выбора значения r (п. 2") в случае, когда одинаковые минимальные значения отношения

будут достигнуты для нескольких строк таблицы Т ( q ) одновременно. Тогда на следующей итерации столбец b (β( q +1)) будет содержать нулевые элементы. Напомним, что
F F допустимый базисный план канонической задачи ЛП, соответствующий базису β( q ), называется вырожденным, если некоторые его базисные компоненты равны нулю, т. е. вектор b (β( q )) содержит нулевые элементы.
Задача ЛП, имеющая вырожденные планы, называется вырожденной. При «выходе» на вырожденный план мы фактически получаем разложение столбца b по системе из меньшего, чем m, количества столбцов аj и, следовательно, лишаемся возможности корректно определить, ввод какого столбца в базис приведет к росту значения целевой функции. Подобные ситуации, в конечном счете, могут привести к зацикливанию вычислительного процесса, т. е. бесконечному перебору одних и тех же базисов.
С точки зрения первой геометрической интерпретации ЗЛП ситуация вырожденности означает, что через некоторую угловую точку многогранного множества допустимых планов задачи, соответствующую текущему базисному плану, проходит более чем m гиперплоскостей ограничений задачи. Иными словами, одно или несколько ограничений в данной точке являются избыточными. Последнее предоставляет повод для размышлений об экономической стороне проблемы вырожденности как проблемы наличия избыточных ограничений и в некоторых случаях определяет пути ее решения.
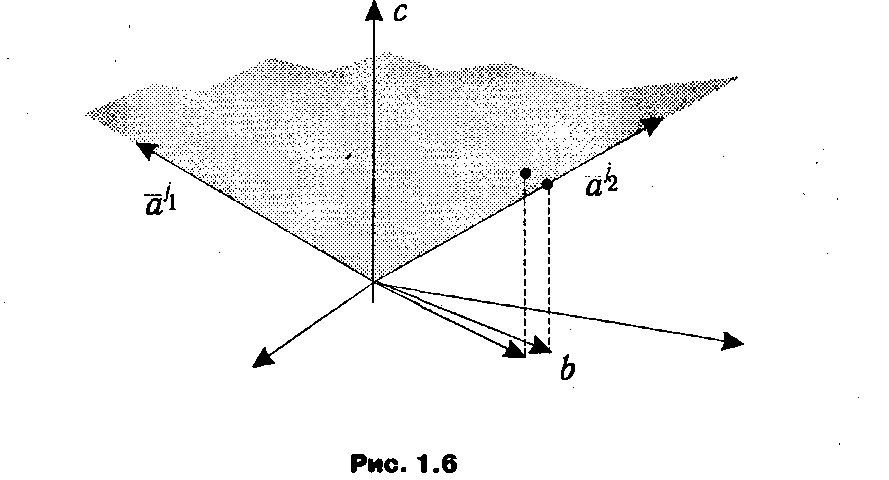
С точки зрения второй геометрической интерпретации ЗЛП вырожденность означает «попадание» линии, проходящей через вершину вектора b параллельно оси аппликат, в ребро конуса, натянутого на систему расширенных векторов текущего базиса. Так, в случае, изображенном на рис. 1.6, эта линия попадает в ребро, определяемое вектором аj 2, т. е., несмотря на то что текущий базис содержит столбцы аj 1 и аj 2, для представления вектора b достаточно только одного аj 2.
Из данной интерпретации вытекает и идея метода решения вырожденных задач ЛП, получившего названия метода возмущений: при выходе на вырожденный план осуществляется незначительный сдвиг вектора b и вырожденность (как это видно из иллюстрации) устраняется.
Необходимо, однако, сказать, что рассмотренная здесь проблема зацикливания для большинства практически значимых задач является достаточно редкой и маловероятной. Более того, она очень часто разрешается за счет ошибок округлений при выполнении расчетов на ЭВМ.
1.4.5. Нахождение допустимого базисного плана. В рассмотренном выше примере исходный базисный план, необходимый для начала вычислений по симплекс-методу, был подобран за счет особенностей матрицы условий. Действительно, данная матрица уже содержала необходимое количество «почти базисных» столбцов. Очевидно, что для подавляющего большинства задач ЛП невозможно подобным образом сразу и в явном виде указать исходный допустимый базисный план. Вообще говоря, существуют различные приемы решения данной задачи. Мы остановимся на одном из них, получившем название метода минимизации невязок. Его сильной стороной, безусловно, является универсальность. Xотя, в некоторых частных случаях, он может оказаться слишком громоздким.
Идея метода минимизации невязок состоит в построении соответствующей вспомогательной задачи, для которой можно в явном виде указать исходный базисный план, и решении ее с помощью процедуры симплекс-метода.
Не умаляя общности, можно считать, что вектор ограничений в исходной задаче неотрицателен, т. е. bi ≥ 0, i Î 1: m. Тогда для КЗЛП максимизации функции

на множестве, определяемом ограничениями

строится вспомогательная задача

Как видно из (1.36)-(1.39), задача (  ,
, 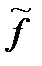 ) отличается от задачи (D, f) матрицей, получаемой в результате добавления к исходной матрице А единичной матрицы, которой соответствуют дополнительные (фиктивные) переменные хn +1,..., хn+m. Данным переменным (собственно говоря, их и называют невязками) в целевой функции
) отличается от задачи (D, f) матрицей, получаемой в результате добавления к исходной матрице А единичной матрицы, которой соответствуют дополнительные (фиктивные) переменные хn +1,..., хn+m. Данным переменным (собственно говоря, их и называют невязками) в целевой функции 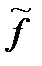 отвечают коэффициенты (-1), а переменным х 1,..., хn, которые являются общими для обеих задач, — нулевые коэффициенты. Существенной особенностью (
отвечают коэффициенты (-1), а переменным х 1,..., хn, которые являются общими для обеих задач, — нулевые коэффициенты. Существенной особенностью (  ,
, 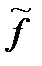 ) является наличие в ней очевидного исходного базиса, образуемого добавленными столбцами, и соответствующего плана с базисными компонентами х n+i = bi ≥ 0, i Î 1: m. В силу структуры целевой функции f̃ в процесс поиска ее максимума процедурой симплекс-метода фиктивные переменные (невязки) х n+i должны минимизироваться желательно до нуля, что может быть достигнуто за счет последовательного перевода их в небазисные компоненты плана. Если в оптимальном плане х̃, полученном в результате решения вспомогательной задачи, последние m компонент (т. е. невязки) равны нулю, то его начальные n компонент удовлетворяют системе ограничений, определяющих область D, и
) является наличие в ней очевидного исходного базиса, образуемого добавленными столбцами, и соответствующего плана с базисными компонентами х n+i = bi ≥ 0, i Î 1: m. В силу структуры целевой функции f̃ в процесс поиска ее максимума процедурой симплекс-метода фиктивные переменные (невязки) х n+i должны минимизироваться желательно до нуля, что может быть достигнуто за счет последовательного перевода их в небазисные компоненты плана. Если в оптимальном плане х̃, полученном в результате решения вспомогательной задачи, последние m компонент (т. е. невязки) равны нулю, то его начальные n компонент удовлетворяют системе ограничений, определяющих область D, и  легко (простым отбрасыванием невязок) может быть преобразован в стартовый допустимый план основной задачи (D, f). При этом все строки симплекс-таблицы, полученной на последней итерации вспомогательной задачи (за исключением нулевой), могут быть перенесены в первую таблицу основной задачи. Элементы же нулевой строки для вновь формируемой симплекс-таблицы вычисляются по формулам:
легко (простым отбрасыванием невязок) может быть преобразован в стартовый допустимый план основной задачи (D, f). При этом все строки симплекс-таблицы, полученной на последней итерации вспомогательной задачи (за исключением нулевой), могут быть перенесены в первую таблицу основной задачи. Элементы же нулевой строки для вновь формируемой симплекс-таблицы вычисляются по формулам:

где β(*) — базис, полученный на последней итерации вспомогательной задачи.
В случае, когда оптимальный план вспомогательной задачи х̃ все же содержит не равные нулю фиктивные компоненты (т. е.  (
(  )<0), мы приходим к заключению об отсутствии допустимых планов у исходной задачи (D, f), т. е. D = Ø.
)<0), мы приходим к заключению об отсутствии допустимых планов у исходной задачи (D, f), т. е. D = Ø.
 2018-01-08
2018-01-08 2771
2771
