1.2.1. Основные понятия линейной алгебры и выпуклого анализа, применяемые в теории математического программирования. Кратко напомним некоторые фундаментальные определения и теоремы линейной алгебры и выпуклого анализа, которые широко применяются при решении проблем как линейного, так и нелинейного программирования.
Фундаментальным понятием линейной алгебры является линейное (вещественное) пространство. Под ним подразумевается множество некоторых элементов (именуемых векторами или точками), для которых заданы операции сложения и умножения на вещественное число (скаляр), причем элементы, являющиеся результатом выполнения операций, также в соответствии с определением должны принадлежать исходному пространству.
Частными случаями линейных пространств являются вещественная прямая, плоскость, геометрическое трехмерное пространство.
Вектор λ1 a 1 + λ2 a 2 + …+ λm a m называется линейной комбинацией векторов а 1 а 2,..., а m с коэффициентами λ1, λ2, λm,
Система векторов линейного пространства а 1 а 2,..., а m называется линейно зависимой, если существуют такие числа λ1, λ2, λm не равные одновременно нулю, что их линейная комбинация λ1a1 + λ2a2 + …+ λmam равняется нулевому вектору (вектору, все компоненты которого равны нулю). В противном случае систему а 1, а 2,..., а m называют линейно независимой, т. е. линейная комбинация данных векторов может быть равна нулевому вектору только при нулевых коэффициентах λ1, λ2, …, λm
Максимально возможное количество векторов, которые могут образовывать линейно независимую систему в данном линейном пространстве, называют размерностью пространства, а любую систему линейно независимых векторов в количестве, равном размерности, — базисом пространства.
Линейное пространство обычно обозначают как Rn, где n — его размерность.
Любое подмножество данного линейного пространства, которое само обладает свойствами линейного пространства, называется линейным подпространством. Множество Н, получаемое сдвигом некоторого линейного подпространства L Ì Rn на вектор a Î Rn: H=L+a, называется аффинным множеством (пространством). Если фундаментальным свойством любого линейного пространства или подпространства является принадлежность ему нулевого вектора, то для аффинного множества это не всегда так. На плоскости примером подпространства является прямая, проходящая через начало координат, а аффинного множества — любая прямая на плоскости. Характеристическим свойством аффинного множества является принадлежность ему любой прямой, соединяющей две любые его точки. Размерность аффинного множества совпадает с размерностью того линейного подпространства, сдвигом которого оно получено.
Если рассматривается некоторое линейное пространство Rn, то принадлежащие ему аффинные множества размерности 1 называются прямыми, а размерности (n -1)— гиперплоскостями. Так, обычная плоскость является гиперплоскостью для трехмерного геометрического пространства R3, а прямая — гиперплоскостью для плоскости R 2. Всякая гиперплоскость делит линейное пространство на два полупространства.
Множество V векторов (точек) линейного пространства Rn называется выпуклым, если оно содержит отрезок прямой, соединяющей две его любые точки, или, другими словами, из того, что a ÎV и bÎV, следует, что х = (1- λ) х а+ λ х b Î V, где 0 ≤λ≤ 1.
Линейная комбинация
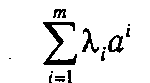
векторов а 1, а 2... а m называется выпуклой, если λ i ≥0, iÎ1: m и
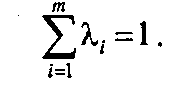
Множество, содержащее все возможные выпуклые комбинации точек некоторого множества М, называют выпуклой оболочкой данного множества. Можно показать, что выпуклая оболочка множества М является наименьшим выпуклым множеством, содержащим М.
Выпуклая оболочка конечного множества точек называется выпуклым многогранником, а непустое пересечение конечного числа замкнутых полупространств — многогранным выпуклым множеством. В отличие от выпуклого многогранника последнее может быть неограниченным.
Точка v выпуклого множества V называется его угловой (крайней) точкой, если она не является внутренней точкой ни для какого отрезка, концы которого принадлежат множеству V. Угловые точки выпуклого многогранника являются его вершинами, а сам он — выпуклой оболочкой своих вершин.
Множество К называется конусом с вершиной в точке x0, если x 0 Î К, и из того, что некоторая точка х принадлежит К (х Î К), следует, что в К содержится и луч, начинающийся в х0 и проходящий через х, т. е.
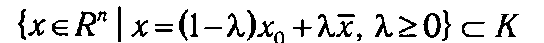
или
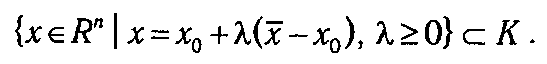
Выпуклая оболочка конечного множества лучей, исходящих из одной точки, называется многогранным выпуклым конусом с вершиной в данной точке.
1.2.2. Первая геометрическая интерпретация ЗЛП и графический метод решения. Рассмотрим следующий пример. Пусть дана задача максимизации линейной целевой функции
f(x) = 3 х 1 + х 2 → max
на множестве
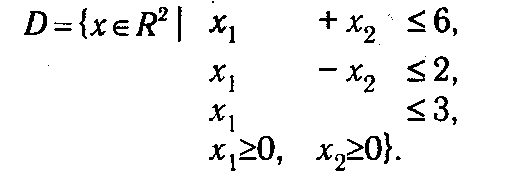
Так как количество переменных в неравенствах, задающих область допустимых планов задачи, равно двум, то ее можно изобразить на координатной плоскости (см. рис. 1.1).
На рис. 1.1 показано, что каждое неравенство определяет некоторую полуплоскость. Соответствующие области для каждого ограничения отмечены штрихами. Пересечение D данных полуплоскостей (т. е. множество точек, которые одновременно принадлежат каждой их них) является областью допустимых планов задачи. Поведение целевой функции f(x) = 3 х 1 + х 2 в рамках двумерной иллюстрации может быть охарактеризовано с помощью линий уровня.
Напомним, что линией уровня функции называется множество точек из ее области определения, в которых функция принимает одно и то же фиксированное значение. Градиентом функции f(x) называется вектор
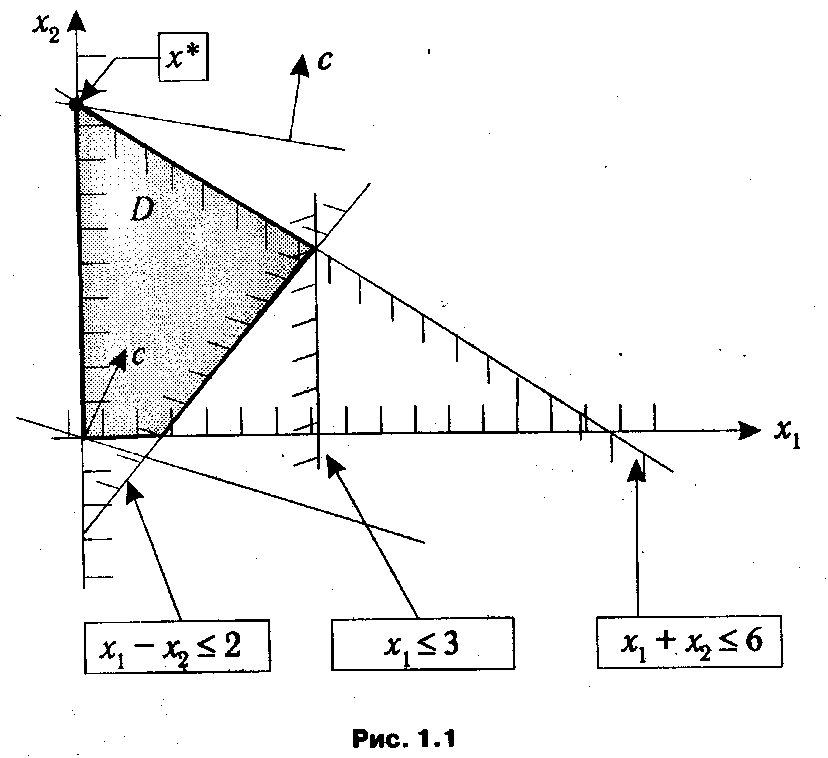
Δ f(x) = df,…, df
dx 1 dxn
указывающий направление наиболее быстрого возрастания функции, и, стало быть, ориентированный перпендикулярно линиям уровня.
Для линейной функции двух переменных линия уровня представляет собой прямую, перпендикулярную вектору с, который служит градиентом данной функции. Следовательно, если линия уровня определяется уравнением f(x)=c1x1+ c2x2 =const, то этот вектоp имеет вид
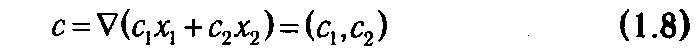
и указывает направление возрастания функции.
Таким образом, с геометрической точки зрения задача максимизации сводится к определению такой точки области D, через которую проходит линия уровня, соответствующая наибольшему из возможных значений. Последнее означает, что для нахождения точки экстремума в задаче линейного программирования мы должны сначала построить линию уровня для некоторого произвольного значения целевой функции. Затем необходимо осуществлять ее параллельное передвижение (так, чтобы она оставалась перпендикулярной вектору с) до тех пор, пока не достигнем такой точки области допустимых планов D, из которой смещение в направлении вектора с было бы невозможно. Такой метод решения получил название графического. Заметим, что решение задачи поиска минимума линейной функции осуществляется аналогично, с той лишь разницей, что движение по линиям уровня должно производиться в направлении, обратном градиенту целевой функции, т. е. по вектору (-с).
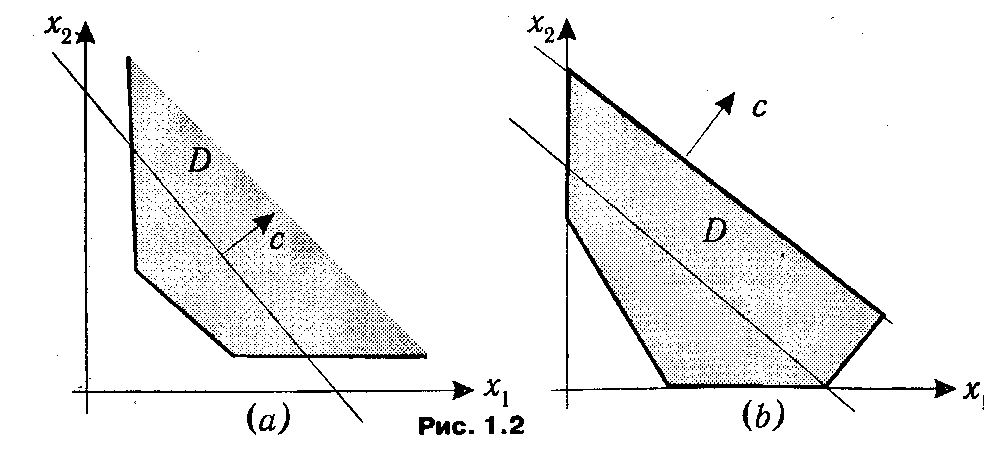
На рис. 1.1 изображен некоторый частный случай, для которого решение ЗЛП достигается в угловой точке х* = (0, 6) области D. Нетрудно представить, что возможны и другие варианты. Они изображены на рис. 1.2.
Рисунок (а) иллюстрирует ситуацию неограниченности целевой функции f(x)=cx на множестве D, т.е. сколько бы мы ни перемещались по линиям уровня в направлении вектора с, ее значение будет возрастать.
В случае, изображенном на рисунке (b), линия уровня, соответствующая максимальному значению f(x), касается грани множества D, и, соответственно, все точки, лежащие на этой грани, являются оптимальными планами.
Во всех рассмотренных иллюстрациях допустимые планы ЗЛП представлялись в виде некоторого многогранного выпуклого множества на плоскости. Такое их представление в литературе получило название первой геометрической интерпретации задачи линейного программирования.
Заметим также, что аналогичным образом могут быть построены интерпретации ЗЛП для случая трехмерного пространства R 3, где множеству D будет соответствовать некоторый ограниченный или неограниченный многогранник, а поведение целевой функции будет характеризоваться поверхностями (плоскостями) уровня.
Несмотря на свою очевидную ограниченность, графический метод решения ЗЛП часто оказывается полезным. В частности, он может быть применен не только к задачам с двумя переменными и ограничениями в виде неравенств, но и к каноническим задачам вида (1.7), у которых n - m = 2, где n — количество переменных, а m — ранг матрицы А.
Действительно, можно выбрать две произвольные переменные хj1,xj2 и, используя систему уравнений, выразить через них остальные переменные
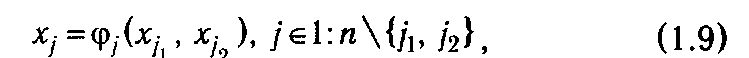
где φj(xj 1, xj 2) —линейные функции.
Подставив выражения (1.9) в целевую функцию, мы получим эквивалентную задачу

при ограничениях
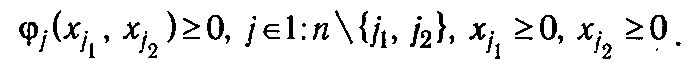
Последняя ЗЛП может быть решена графически.
1.2.3. Основные теоремы линейного программирования. Рассмотрим некоторые теоремы. Отражающие фундаментальные свойства задач линейного программирования и лежащие в основе методов их решения. Они по существу обобщают на случай задач с произвольным количеством переменных те свойства, которые мы наблюдали в двумерном случае.
Теорема 1.1. Если целевая функция f принимает максимальное значение в некоторой точке множества допустимых планов D, то она принимает это значение и в некоторой угловой точке данного множества.
Доказательство.
Чтобы не усложнять изложение, ограничимся тем случаем, когда множество D ограничено, и, следовательно, является выпуклым многогранником.
Для доказательства воспользуемся следующим известным свойством ограниченных выпуклых множеств:
| Если D — замкнутое ограниченное выпуклое множество, имеющее конечное число угловых точек, то любая точка х Î D может быть представлена в виде выпуклой комбинации угловых точек D*. |
* Строгое доказательство данного утверждения см., например, в [14].
Пусть х 1, х 2,…, хm — угловые точки множества D, а х* — точка, в которой целевая функция f достигает максимума.
На основе сформулированного выше утверждения точку х* можно представить в виде выпуклой комбинации угловых точек х 1, х 2,..., xm
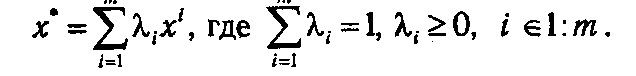
Так как х* — точка максимума, то для любого х Î D сх* ≥ сх. Функция f(x) — линейная, поэтому
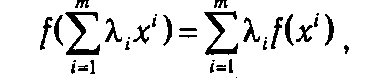
cледовательно,
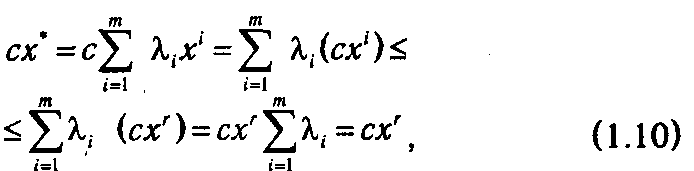
где xr — угловая точка, удовлетворяющая условию
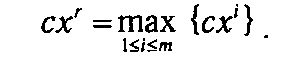
Из (1.10) видно, что сх* ≤ схr. В то же время справедливо обратное неравенство: сх* ≥ схr. Откуда следует, что сх* = схr, т. е. существует по крайней мере одна угловая точка хr, в которой целевая функция принимает максимальное значение. A
| Теорема 1.2. Если целевая функция f принимает максимальное значение в нескольких точках множества D, то она принимает это же значение в любой точке, являющейся их выпуклой комбинацией. |
Доказательство.
Пусть максимальное значение функции f достигается в точках х̃ 1, х̃ 2,..., x̃s, т. е. сх~i=f*, iÎ l :s. Рассмотрим произвольную выпуклую комбинацию этих точек
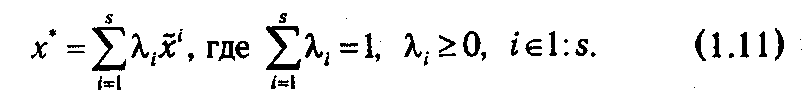
Найдем значение целевой функции в точке х*
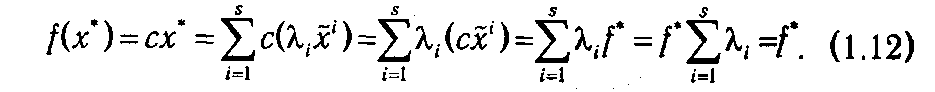
Итак, для произвольной выпуклой комбинации х* точек х̃1, х̃ 2,..., x~s справедливо равенство

 2018-01-08
2018-01-08 1330
1330
