Формы задачи линейного программирования

В общем виде задача линейного программирования* (в дальней­шем ЗЛП) может быть сформулирована как задача нахождения наибольшего значения линейной функции

 

 

на некотором множестве D Ì Rⁿ, где х Î D удовлетворяют сис­теме ограничений

 

 

и, возможно, ограничениям

х ₁ ≥0, х ₂ ≥0,..., х_j ≥0,..., х_n ≥0. (1.3)

* Напомним, что частные примеры, сводящиеся к задаче линейного программирования, были описаны во введении.

 

Не умаляя общности, можно считать, что в системе (1.2) пер­вые m ограничений являются неравенствами, а последующие — l -уравнениями. Очевидно, этого всегда можно добиться за счет простого переупорядочения ограничений. Относительно направ­ления знака неравенства будем предполагать, что левая часть меньше или равна правой. Добиться этого можно, умножив на (-1) обе части тех неравенств, которые имеют противопо­ложный знак. Ограничения (1.3), вообще говоря, могут быть рассмотрены как частный случай ограничений в форме нера­венств, но в силу особой структуры их обычно выделяют от­дельно и называют условиями неотрицательности (или три­виальными ограничениями).

Дополнительно следует заметить, что выбор типа искомого экстремума (максимума или минимума) также носит относитель­ный характер. Так, задача поиска максимума функции

 

 

эквивалентна задаче поиска минимума функции

 

 

Часто условия задачи (1.1)-(1.3), содержащей ограничения только типа неравенств, бывает удобно записывать в сокращен­ной матричной форме

 

f(x) = сх → max, A_x ≤ b, х ≥ 0, (1.6)

 

где с и х — векторы из пространства Rⁿ, b — вектор из простран­ства R^m, а А — матрица размерности m х n.

Задачу линейного программирования, записанную в форме (1.1)-(1.3), называют общей задачей линейного програм­мирования (ОЗЛП).

Если все ограничения в задаче линейного программирования являются уравнениями и на все переменные х_j наложены усло­вия неотрицательности, то она называется задачей линейного программирования в канонической форме, или канонической задачей линейного программирования (КЗЛП). В матрич­ной форме КЗЛП можно записать в следующем виде:

 

Поскольку любая оптимизационная задача однозначно оп­ределяется целевой функцией f и областью D, на которой отыс­кивается оптимум (максимум), будем обозначать эту задачу парой (D, f).

Условимся относительно терминологии, которая использу­ется в дальнейшем и является общепринятой в теории линейно­го программирования.

Планом ЗЛП называется всякий вектор х из пространства Rⁿ.

Допустимым планом называется такой план ЗЛП, кото­рый удовлетворяет ограничениям (1.2)-(1.3), т. е. содержится в области D. Сама область D называется при этом областью допустимых планов. Оптимальным планом х* называется такой допустимый план, при котором целевая функция достигает оптимального (в нашем случае — максимального) значения, т. е. план, удовлетворяющий условию

 

max f(x) = f(x*).

 

Величина f* =f(х*) называется оптимальным значением целевой функции.

Решением задачи называется пара (х*, f*), состоящая из oптимального плана и оптимального значения целевой функции, а процесс решения заключается в отыскании множества всех решений ЗЛП.

1.1.2. Переход к канонической форме. Подавляющее боль­шинство известных методов решения задач линейного програм­мирования предназначены для канонических задач. Поэтому начальный этап решения всякой общей задачи линейного про­граммирования обычно связан с приведением ее к некоторой эквивалентной канонической задаче.

Общая идея перехода от ОЗЛП к КЗЛП достаточно проста:

Ø Ø ограничения в виде неравенств преобразуются в уравне­ния за счет добавления фиктивных неотрицательных переменных х_i, (i Î 1 :m), которые одновременно входят в целевую функцию с коэффициентом 0, т. е. не оказывают влияния на ее значение;

Ø Ø переменные, на которые не наложено условие неотрица­тельности, представляются в виде разности двух новых неотрицательных переменных:

- = - =

х_j = х_j – х_j, (x_j ≥ 0, х_j ≥ 0 ).

 

Проиллюстрируем применение описанных выше рекоменда­ций на примере. Пусть задана задача линейного программирова­ния (D, f) в общей форме с целевой функцией

 

f(x) = 5 х ₁ + 3 x ₂ + x ₃ + 2 х ₄ -2 х ₅ → max

 

и множеством допустимых планов D, определенным системой уравнений и неравенств,

 

2 х 1	+ 4 х 2	+ 5 x 3		=7,
	- 3 x 2	+ 4 x 3	– 5 x 4 – 4 x 5	≤ 2,
3 х 1		- 5 x 3	+ 6 x 4 – 2 x 5	≤ 4,
х 1≥ 0,		x 3	≥ 0.

 

Тогда в соответствии со сформулированными правилами эк­вивалентная каноническая задача будет иметь вид (D',f'), где:

 

 

а множество D' определено как:

 

 

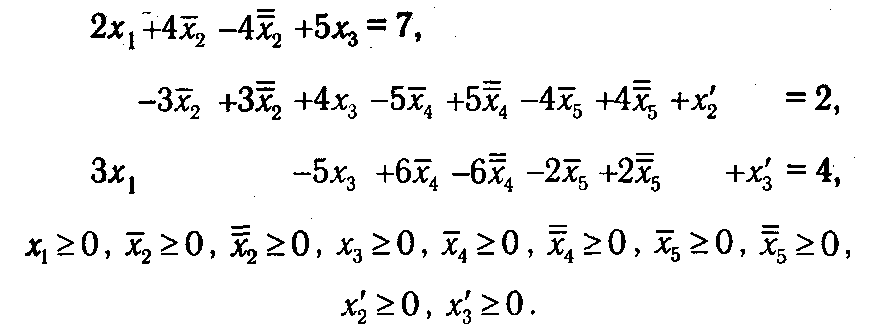
Нетрудно заметить, что «платой» за переход от общей фор­мы задачи линейного программирования к канонической явля­ется рост ее размерности, что, при прочих равных условиях, является фактором, усложняющим процесс решения.