Модифицированный симплекс-метод

1.5.1. Вычислительная схема, основанная на преобразовании обратных матриц. Анализируя вычислительную процедуру симплекс-метода с позиций оценки трудоемкости, нетрудно заметить, что наиболее критичным в этом плане является этап пересчета значений А и b при переходе от одного базисного плана к другому (п. 3 алгоритма). Однако в том случае, когда число ограничений задачи m явно меньше количества переменных n, можно добиться существенной «экономии», выполняя на очередной итерации q преобразование Жордана—Гаусса не над матрицей А (β⁽ ^q ⁾), а над матрицей Δ^-1(β⁽ ^q ⁾). При этом учитывается и то, что при необходимости, применяя формулу (1.26), всегда можно получить А (β⁽ ^q ⁾) по Δ^-1(β⁽ ^q ⁾). Более того, для выполнения описанных выше действий симплекс-процедуры нам в действительности не требовалась матрица А (β⁽ ^q ⁾) целиком. Реально в ней использовались только строка оценок a ₀(β⁽ ^q ⁾) и ведущий столбец a^l (β⁽ ^q ⁾). Данные соображения положены в основу вычислительной схемы симплекс-метода, основанной на преобразовании обратных матриц, которую также называют модифицированным симплекс-методом. Впервые данный алгоритм был предложен в 1951 г. в работах Л. В. Канторовича.

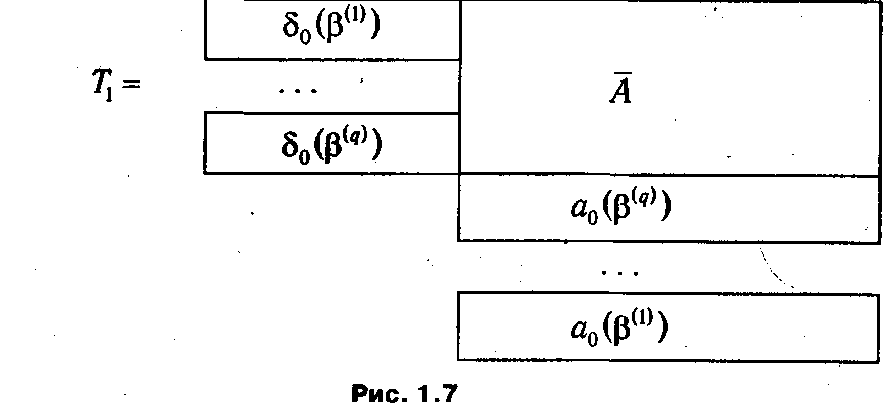
Вычислительной схеме модифицированного симплекс-метода соответствует система таблиц T ₁ и Т ₂⁽ ^q ⁾. Таблица T ₁ (рис. 1.7) является общей для всех итераций и служит для получения строки оценок текущего базисного плана a ₀(β⁽ ^q ⁾). Если обозначить через δ _i (β⁽ ^q ⁾) (i Î 0: m) строки матрицы Δ^-1(β⁽ ^q ⁾), то из (1.26), в частности, следует, что

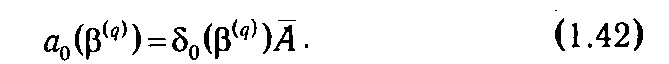
Как видно из рис. 1.7, T ₁ состоит из трех блоков:

Ø Ø в центре содержится матрица А;

Ø Ø в левом блоке таблицы на каждой итерации дописываются нулевые строки матрицы Δ^-1(β⁽ ^q ⁾) для текущего базиса;

Ø Ø нижний блок, расположенный под матрицей А, на каждой итерации дополняется строкой оценок текущего плана, вычисленной по формуле (1.42).

Симплекс-таблица Т ₂⁽ ^q ⁾, изображенная на рис. 1.8, соответствует допустимому базису КЗЛП β⁽ ^q ⁾, получаемому на q -й итерации. Столбец N (β⁽ ^q ⁾) содержит номера базисных столбцов (в последовательности вхождения в базис); столбец b (β⁽ ^q ⁾) — компоненты вектора ограничений относительно текущего базиса β⁽ ^q ⁾; Δ^-1(β⁽ ^q ⁾) — матрица, обратная по отношению к матрице расширенных столбцов текущего базиса β⁽ ^q ⁾; графа а^l содержит расширенный вектор условий, вводимый в базис на текущей итерации, а следующая графа — координаты а^l (β⁽ ^q ⁾) этого же столбца в текущем базисе β⁽ ^q ⁾.

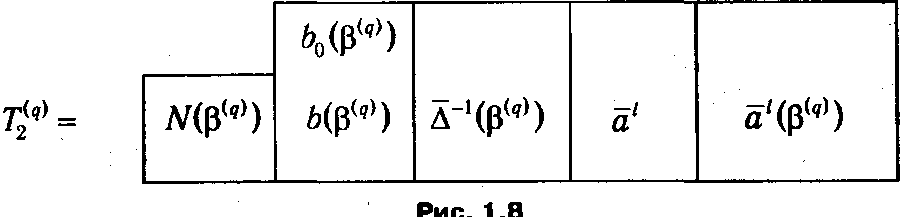
По аналогии с п. 1.4.1 опишем формальную схему алгоритма модифицированного симплекс-метода.

0-этап. Нахождение допустимого базисного плана.

1. Для поиска допустимого базиса может быть применен метод минимизации невязок, рассмотренный в п. 1.4.5. При этом для решения вспомогательной задачи используется процедура модифицированного симплекс-метода. В результате 0-этапа мы получаем допустимый базисный план x (β⁽¹⁾) и соответствующие ему матрицу Δ^-1(β⁽¹⁾) и вектор b (β⁽¹⁾).

2. Заполняем центральную часть таблицы T ₁, содержащую матрицу А.

3. Содержимое матрицы Δ^-1(β⁽¹⁾) и вектора b (β⁽¹⁾), полученных на этапе поиска допустимого базисного плана, переносится в таблицу T ₂⁽¹⁾.

4. Полагаем номер текущей итерации q равным 1 и переходим к I-этапу.

1-этап. Стандартная итерация алгоритма — выполняется для очередного базисного плана x (β⁽ ^q ⁾).

1°. Проверка оптимальности текущего базисного плана. Содержимое нулевой строки таблицы T ₂⁽ ^q ⁾— δ₀(β⁽ ^q ⁾) переписывается в соответствующую графу таблицы T ₁. По формуле (1.42) рассчитываем и заполняем строку a ₀(β⁽ ^q ⁾). Осуществляем просмотр строки оценок a ₀(β⁽ ^q ⁾). Возможны два варианта:

1΄. a ₀(β⁽ ^q ⁾)≥0 —план, соответствующий текущему базису задачи, оптимален. Вычислительный процесс закончен. Согласно формулам (1.33) и (1.32) выписываются оптимальный план задачи х * = x (β⁽ ^q ⁾) и оптимальное значение целевой функции f (х *) = f (x (β⁽ ^q ⁾)).

1". В строке оценок a ₀(β⁽ ^q ⁾) существует по меньшей мере один элемент a _0, _j (β⁽ ^q ⁾)<0, т. е. имеющий отрицательную оценку. Следовательно, план x (β⁽ ^q ⁾) — неоптимален. Выбирается номер l, соответствующий элементу, имеющему минимальную (максимальную по абсолютной величине) отрицательную оценку:

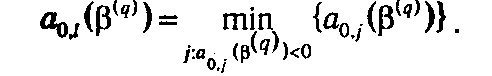
l -й столбец матрицы A становится ведущим и должен быть введен в очередной базис. Переходим к пункту 2° алгоритма.

2°. Определение столбца, выводимого из базиса. Переписываем ведущий столбец а^l из таблицы T ₁ в текущую таблицу Т ₂⁽ ^q ⁾. По формуле а^l (β⁽ ^q ⁾) = Δ^-1(β⁽ ^q ⁾) а^l заполняем соответствующий столбец в таблице Т ₂⁽ ^q ⁾. Возможны два варианта:

2'. Для всех i Î 1: m а_i_,_l (β⁽ ^q ⁾)≤0. Делается вывод о неограниченности целевой функции и завершается вычислительный процесс.

2". Существует по крайней мере один индекс i Î 1: m, для которого а_i_,_l (β⁽ ^q ⁾)>0. Согласно правилу (1.27) определяются место r и номер N_r (β⁽ ^q ⁾) для столбца, выводимого из базиса. Переходим к пункту 3° алгоритма.

3°. Пересчет относительно нового базиса элементов столбца b и матрицы Δ^-1. Переход к новому базису β⁽ ^q ⁺¹⁾, который получается введением в базис β⁽ ^q ⁾ столбца а^l и выводом из него столбца а^r, осуществляется по формулам, аналогичным формулам (1.28)-(1.31). Они имеют вид:

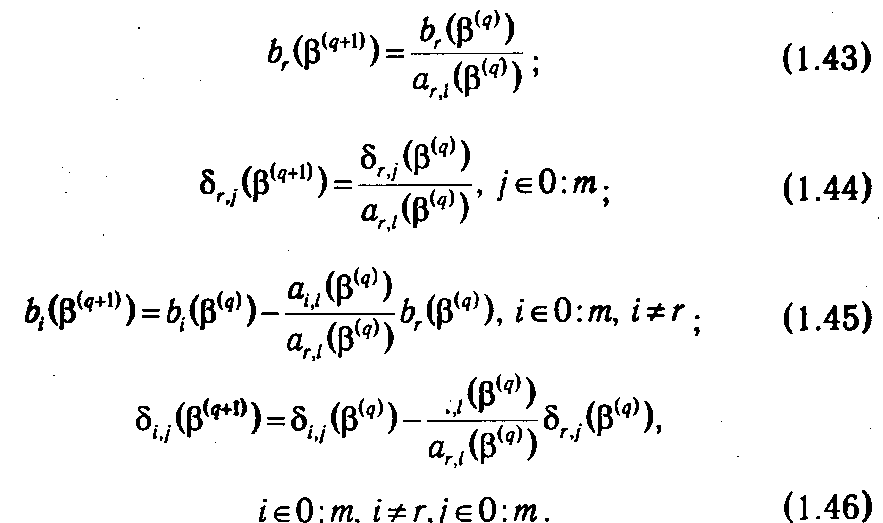
Полагаем номер текущей итерации q: = q +l и переходим к первому пункту алгоритма.

В завершение подчеркнем, что в силу приведенных выше преимуществ именно модифицированный симплекс-метод реально применяется в программном обеспечении, предназначенном для решения канонических задач линейного программирования.

1.5.2. Пример решения ЗЛП модифицированным симплекс-методом. Приведем решение рассмотренной ранее задачи (1.34)-(1.35), основанное на использовании процедуры модифицированного симплекс-метода. По аналогии с п. 1.4.3 оно начинается с выбора очевидного исходного базиса, образуемого столбцами {5,2,3}. Для него уже были вычислены Δ^-1(β⁽ ^q ⁾) и b (β⁽ ^q ⁾), поэтому заполнение начальных таблиц T ₁ и Т ₂⁽¹⁾ не представляет труда.

На первой итерации мы переписываем нулевую строку

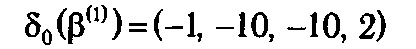
из Т ₂⁽¹⁾ в T ₁ и, умножив ее на матрицу A, получаем строку оценок

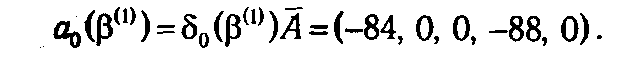
Так как a ₀(β⁽¹⁾) содержит отрицательные элементы, то делаем вывод о неоптимальности плана, соответствующего базису β⁽¹⁾, и, выбрав наименьшую отрицательную оценку (-88), получаем номер столбца, вводимого в базис, l = 4.

Переписываем столбец

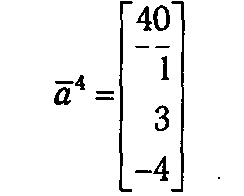
из таблицы T ₁ в Т ₂⁽¹⁾ и пересчитываем его координаты относительно текущего базиса, т. е. умножаем матрицу Δ^-1(β⁽ ^q ⁾), расположенную в таблице Т ₂⁽¹⁾ слева, на а ⁴.

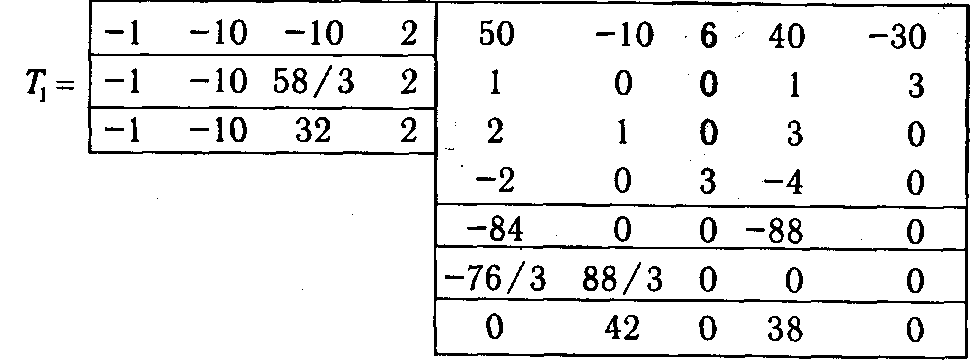
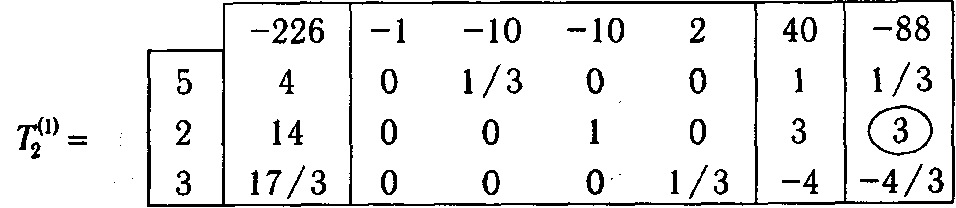
После заполнения таблицы Т ₂⁽¹⁾ данными по вводимому в новый базис столбцу можно перейти к определению номера выводимого столбца. Эта процедура осуществляется в полной аналогии с обычным симплекс-методом. Рассмотрев отношения элементов b_i (β⁽¹⁾) и a_i_,_l (β⁽¹⁾) для { i Î1: m| a_i_,_l (β⁽¹⁾)>0} и определив минимальное из них, находим, что r = 2. Следовательно, столбец с номером N ₂(β⁽ ^q ⁾) = 2 должен быть выведен из базиса. Таким образом, получаем очередной допустимый базис задачи с N (β⁽²⁾) = {5, 4, 3}. Элемент a _2,3(β⁽¹⁾) является ведущим (обведен кружком). Применив формулы (1.43)-(1.46), переходим к симплекс-таблице, соответствующей второй итерации Т ₂⁽²⁾, и полагаем индекс текущей итерации q = 2.

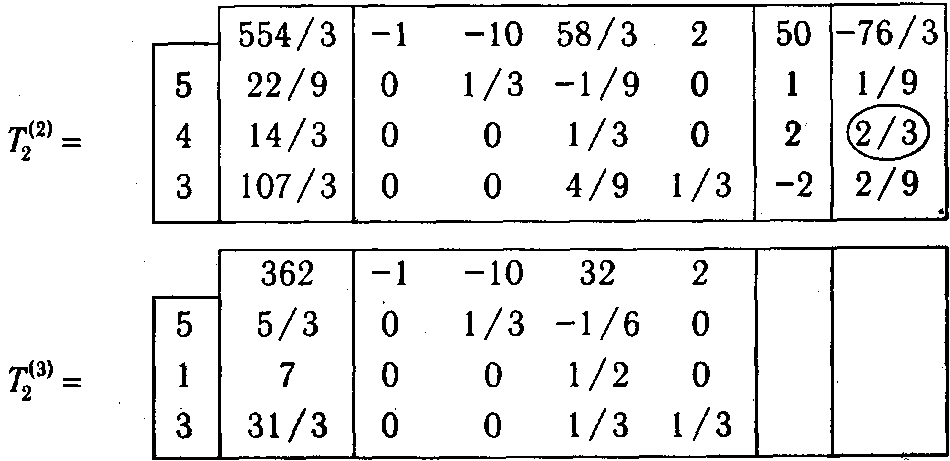
Повторяя те же самые действия (их легко проследить по приводимым здесь таблицам Т ₂⁽²⁾ и Т ₂⁽³⁾, на третьей итерации мы получим оптимальный план задачи и оптимальное значение целевой функции, которые извлекаются из второго столбца таблицы Т ₂⁽³⁾. Легко заметить, что в процессе решения мы «прошли» по той же самой последовательности допустимых базисных планов, которая встречалась в п. 1.4.3.