ВОЛНОВЫЕ СВОЙСТВА СВЕТА
Методические указания к лабораторным работам
по курсу «Общая физика»
Омск
Издательство ОмГТУ
Составители: Э.М. Ярош, Ю.И. Беликов, О.В. Лях, Т.Н. Кондратьева, О.Ю. Павловская, Е.А. Сидорова, С.С. Ясько.
Данные методические указания разработаны для выполнения лабораторных работ на модульном учебном комплексе МУК–О по разделам общей физики: «Волновая оптика», «Тепловое излучение».
Предназначены для студентов всех специальностей ОмГТУ.
Печатается по решению редакционно-издательского совета
Омского государственного технического университета.
Лабораторная работа № 7-14
ИЗУЧЕНИЕ ИНТЕРФЕРЕНЦИИ СВЕТА ОТ ДВУХ ЩЕЛЕЙ
Цель работы: определение расстояния между щелями с помощью интерференционных полос.
Приборы и принадлежности: модульный лабораторный учебный комплекс МУК – О, миллиметровая линейка, лист белой бумаги.
Краткая теория
Интерференцией света называется явление перераспределения световой энергии в пространстве при сложении (суперпозиции) колебаний от нескольких источников когерентных волн. Рассмотрим два точечных когерентных источника 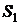 и
и 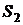 , колебания которых происходят с одинаковой частотой, а разность фаз колебаний равна нулю (источники синфазны). Пусть от источника
, колебания которых происходят с одинаковой частотой, а разность фаз колебаний равна нулю (источники синфазны). Пусть от источника 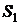 распространяются бегущие волны в среде 1 с показателем преломления
распространяются бегущие волны в среде 1 с показателем преломления 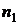 , а от источника
, а от источника 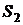 – в среде 2 с показателем преломления
– в среде 2 с показателем преломления 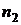 (рис. 1). На рисунке линия
(рис. 1). На рисунке линия 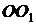 – граница между этими прозрачными средами.
– граница между этими прозрачными средами.
|
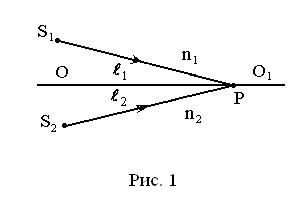 На границе
На границе 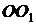 выберем точку
выберем точку  и определим условие минимума и максимума амплитуды результирующего колебания в этой точке пространства. Обозначим
и определим условие минимума и максимума амплитуды результирующего колебания в этой точке пространства. Обозначим 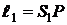 ,
, 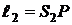 . Для электромагнитных волн (свет – электромагнитная волна) колебания вектора
. Для электромагнитных волн (свет – электромагнитная волна) колебания вектора 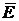 от двух одинаковых источников 1 и 2 определяются выражениями:
от двух одинаковых источников 1 и 2 определяются выражениями: 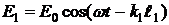 и
и 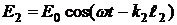 , где
, где  – амплитуда гармонических колебаний,
– амплитуда гармонических колебаний,  – волновое число,
– волновое число, 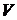 – скорость распространения волны.
– скорость распространения волны.
В точке наблюдения  происходит сложение колебаний одинаковой частоты. Будем считать, что эти колебания происходят вдоль одного направления. Разность фаз колебаний в этой точке равна:
происходит сложение колебаний одинаковой частоты. Будем считать, что эти колебания происходят вдоль одного направления. Разность фаз колебаний в этой точке равна:
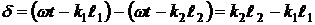 ,
,
где 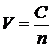 – скорость распространения электромагнитной волны в среде с показателем преломления
– скорость распространения электромагнитной волны в среде с показателем преломления 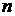 ;
; 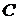 – скорость этой волны в вакууме. Так как
– скорость этой волны в вакууме. Так как
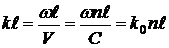 ,
,
где 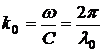 – волновое число для среды с
– волновое число для среды с 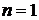 (вакуум),
(вакуум), 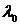 – длина волны в среде с
– длина волны в среде с 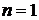 , то разность фаз колебаний
, то разность фаз колебаний
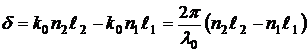
определяет результирующее колебание в точке  .
.
Величина 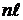 – оптический путь волны. Разность этих величин для двух волн
– оптический путь волны. Разность этих величин для двух волн 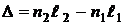 называют оптической разностью хода волн и
называют оптической разностью хода волн и 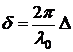 . Из условия минимума при сложении колебаний
. Из условия минимума при сложении колебаний 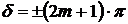 ,
, 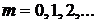 (колебания происходят в противофазе) получится
(колебания происходят в противофазе) получится 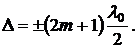 Из условия максимума –
Из условия максимума – 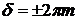 (колебания происходят в одной фазе) определяют условие максимума для
(колебания происходят в одной фазе) определяют условие максимума для 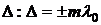 .
.
Можно сказать, что при сложении колебаний в любой точке пространства результирующее колебание определяется величиной оптической разности хода волн.
Методика эксперимента
|
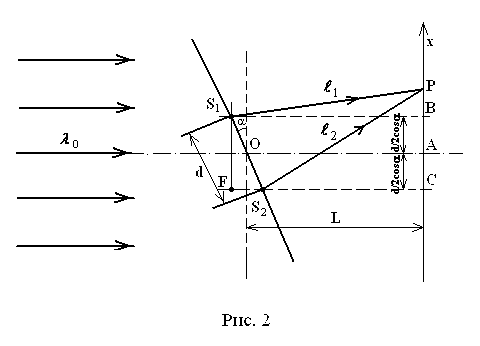 |
Рассмотрим монохроматическую световую волну (длина волны в вакууме
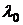 ) с плоским фронтом, падающую на непрозрачный экран с двумя узкими щелями (оптическая схема, близкая к схеме опыта Юнга). Пусть экран, где расположены щели (точечные когерентные источники
) с плоским фронтом, падающую на непрозрачный экран с двумя узкими щелями (оптическая схема, близкая к схеме опыта Юнга). Пусть экран, где расположены щели (точечные когерентные источники 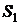 и
и 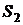 ), может поворачиваться относительно точки
), может поворачиваться относительно точки 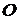 – середины расстояния
– середины расстояния 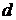 между источниками
между источниками 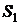 и
и 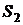 (рис. 2) на некоторый угол
(рис. 2) на некоторый угол 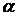 .
.
Экран наблюдения (обычный лист бумаги) располагается на расстоянии 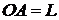 , отсчитываемом от точки
, отсчитываемом от точки 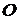 ,
, 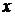 – координата точки наблюдения
– координата точки наблюдения  равна расстоянию
равна расстоянию 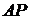 .
.
Рассмотрим две световые волны, прошедшие сквозь щели. Оптическая разность хода двух волн от плоского фронта падающей волны до щелей равна 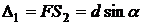 , а оптическая разность хода волн после прохождения щелей равна
, а оптическая разность хода волн после прохождения щелей равна  (
( ). На экран две волны приходят с разностью хода
). На экран две волны приходят с разностью хода 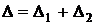 . Рассчитаем
. Рассчитаем 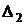 . Из прямоугольных треугольников
. Из прямоугольных треугольников  и
и  :
:
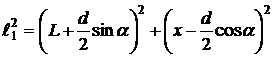 ,
,
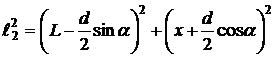 ,
, 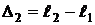 ,
,
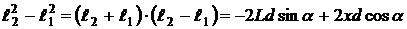 .
.
При условии 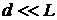 :
: 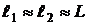 :
:
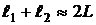 ,
,
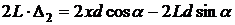 ,
,
или
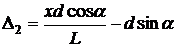 .
.
Тогда
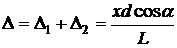 .
.
Из условия максимума для интерферирующих волн – 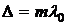 , где
, где 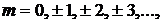 получим
получим 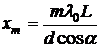 – координаты точек экрана с максимальной интенсивностью света. Расстояние между ними
– координаты точек экрана с максимальной интенсивностью света. Расстояние между ними 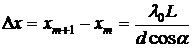 . Измеряя
. Измеряя 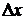 между серединами ярких полос, можно рассчитать расстояние между щелями
между серединами ярких полос, можно рассчитать расстояние между щелями 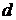 :
:
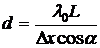 . (1)
. (1)
 2018-01-08
2018-01-08 522
522







