 n q n q | ||||
| 3,832 | 7,016 | 10,173 | 13,324 | |
| 1,841 | 5,331 | 8,836 | 11,706 | |
| 3,054 | 6,706 | 9,969 | 13,170 | |
| 4,201 | 8,015 | 11,346 | 14,586 |
Рассмотрим волны электрического типа. Отыскав решения уравнений (11) и (12), запишем решение уравнения (9)
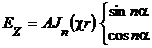 | (14) |
Граничное условие (7) будет выполнено в том случае, когда поперечное волновое число будет удовлетворять соотношению:
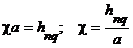 | (15) |
Здесь n - номер функции Бесселя, q - порядковый номер корня уравнения 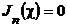 .
.
Зная поперечное волновое число, можно из соотношения
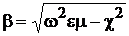
определить фазовую скорость волны типа E в волноводе:
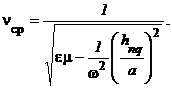
Величина 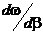 называется групповой скоростью волны (с такой скоростью в волноводе осуществляется перенос энергии).
называется групповой скоростью волны (с такой скоростью в волноводе осуществляется перенос энергии).
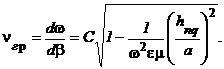
Из этих выражений видно, что фазовая скорость волн в волноводе всегда больше скорости света 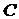 и изменяется (при изменении частоты) в пределах от бесконечности до
и изменяется (при изменении частоты) в пределах от бесконечности до 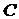 . Частота, на которой фазовая скорость обращается в бесконечность (
. Частота, на которой фазовая скорость обращается в бесконечность (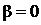 ), называется критической частотой. Групповая скорость изменяется в пределах от нуля на критической частоте до
), называется критической частотой. Групповая скорость изменяется в пределах от нуля на критической частоте до 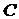 на бесконечно большой частоте.
на бесконечно большой частоте.
Волны электрического типа обозначаются Enq. Физический смысл индексов: n - количество полных периодов поля по азимутальной координате (или количество максимумов одного знака), q - число максимумов поля по радиальной координате.
Волны типа H в круглом волноводе описываются уравнением типа (6) относительно продольной составляющей магнитного поля (в этом уравнении необходимо произвести замену E Z на H Z). Волна типа H имеет одну тангенциальную по отношению к ограничивающей поверхности компоненту электрического поля:
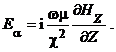
Чтобы выполнялось граничное условие (7), необходимо соблюдать граничное условие для волн типа Н:
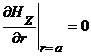 | (16) |
(16) является граничным условием для волн типа H.
Решение уравнения Гельмгольца относительно составляющей поля H Z:
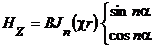 | (17) |
Для того, чтобы граничное условие (16) было выполнено, поперечное волновое число c должно определяться соотношением:
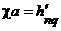 или или 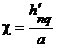 | (18) |
где 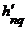 - корень уравнения
- корень уравнения 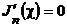 , n - порядок функции Бесселя, q - порядковый номер корня.
, n - порядок функции Бесселя, q - порядковый номер корня.
Фазовая и групповая скорости волн типа H определяются соотношениями, которые были получены для волн типа E, в них нужно лишь сделать замену 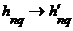 .
.
Распределения полей волн в круглом волноводе
а) Волны типа E
Составляющие электромагнитного поля волн типа E, используя (3), можно записать в следующем виде:
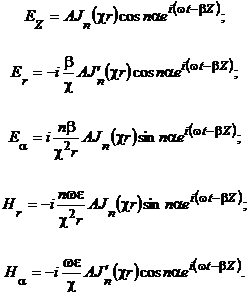 | (19) |
Волны, у которых отсутствует зависимость составляющих поля от азимутальной координаты (n =0), называются симметричными. Из (19) видно, что поле симметричных волн типа E имеет только три составляющие: E Z; E r; H a:

Рис. 3
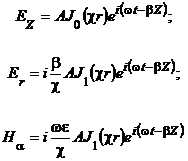 | (20) |
В формулах (20) учтено, что 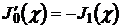 .
.
На рис.3 приведены структуры полей волн E 01; E 11; E 21.
б) Волны типа H
Составляющие электромагнитного поля волн типа H (3) в общем случае можно записать следующим образом:
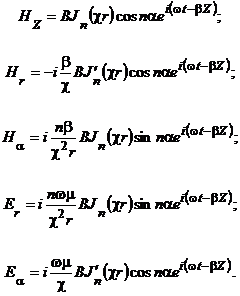 | (21) |
Волны типа H также могут быть симметричными. В этом случае поле имеет три составляющие: H z; Hr; E a.
Отметим, что в выражениях (19), (21) через 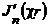 обозначена производная по всему аргументу.
обозначена производная по всему аргументу.
Структуры силовых линий полей волн типа H 01; H 11; H 21 приведены на рис.4. Рассматривая структуры полей E и H, можно отметить общие их особенности:
1. Поперечные составляющие электрического и магнитного полей синфазны и сдвинуты относительно продольных составляющих полей на 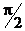 . (О сдвиге фаз говорит множитель i перед поперечными составляющими.)
. (О сдвиге фаз говорит множитель i перед поперечными составляющими.)
2. На стенке волновода касательные составляющие электрического поля равны нулю. Поэтому электрические силовые линии направлены перпендикулярно металлической поверхности.

Рис. 4
3. Магнитные силовые линии на стенках волновода имеют лишь касательные составляющие. Это можно пояснить следующим образом. Из-за действия в диапазоне СВЧ сильного скин-эффекта электромагнитное поле не проникает внутрь металла. Предположим, что на металлической поверхности нормальная составляющая вектора H не равна нулю. Тогда, в силу граничного условия 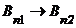 , магнитное поле должно существовать внутри проводника, что на самом деле невозможно.
, магнитное поле должно существовать внутри проводника, что на самом деле невозможно.
 2018-01-08
2018-01-08 1990
1990








