2018-01-08
1982
Круглый волновод представляет собой полую металлическую трубу (рис.1). Будем полагать, что волновод имеет бесконечную длину, а проводимость его экранирующей поверхности 
.
Рис. 1
В волноводе возможно распространение продольно-поперечных волн двух типов:
а) волны, у которых имеется продольная составляющая поля H и отсутствует продольная составляющая поля E (волны типа H);
б) волны, у которых имеется продольная составляющая поля E и отсутствует продольная составляющая поля H (волны типа E).
Исследование круглого волновода целесообразно производить в цилиндрической системе координат, поскольку стенки круглого волновода совпадают с координатной поверхностью r = a. В этой системе будет проще всего записать граничные условия краевой задачи о распространении электромагнитных волн в волноводе.
В дальнейшем будем интересоваться электромагнитными полями, изменяющимися во времени по гармоническому закону. Для областей пространства, где отсутствуют источники поля для комплексных амплитуд можно записать уравнения Максвелла:
|
|
|
| (1) |
или в развернутой форме:
| (2) |
Из уравнений (2) поперечные компоненты поля можно выразить через продольные:
| (3) |
где 
- продольное волновое число, 
- фазовая скорость волны в волноводе, c - поперечное волновое число. Волновые числа связаны между собой соотношением:
При получении формул (3) из (2) предполагалось, что зависимость поля от продольной координаты имеет следующий вид:
| (4) |
Для того, чтобы рассчитать электромагнитное поле для волн типа 
, достаточно решить уравнение Гельмгольца только для продольной составляющей электрического поля:
| (5) |
или, учитывая (4)
| (6) |
В дальнейшем будем использовать обозначение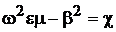 
.
Определив продольную составляющую поля E, поперечные составляющие полей E и H определяем, используя формулы (3).
Аналогичным образом решается задача о расчете электромагнитного поля волн типа H: сначала решается уравнение Гельмгольца для продольной составляющей HZ, а после этого, используя формулы (3), определяются поперечные составляющие.
Волны типа E
Волны типа E в круглом волноводе описываются уравнением (6), которое решается при граничном условии E t/S =0 (Еt - касательная по отношению к поверхности S компонента электрического поля; S - экранирующая поверхность волновода). Это граничное условие является следствием идеальной проводимости стенок волновода (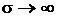
). Действительно, если 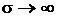, по стенкам волновода будут протекать конечные по величине токи 
только в том случае, если
| (7) |
Поле волны типа E имеет две касательные к стенкам волновода компоненты электрического поля: EZ и Ea. Как следует из (3),
|
|
|
Ea ~ 
.
Не трудно убедиться, что граничное условие (7) будет выполнено в том случае, когда 
. (Сделать соответствующие преобразования и убедиться в том, что 
, если предлагается самостоятельно при подготовке к работе.)
Таким образом, уравнение (6) будем решать при граничном условии .
Решение уравнения (6) будем производить методом разделения переменных. Решение (используем функцию 
) записываем в виде:
| (8) |
Подставив (8) в (6), получаем:
| (9) |
Умножив (9) на r 2 и поделив на 
, получаем:
| (10) |
Для того, чтобы уравнение (10) удовлетворялось тождественно и чтобы поле имело непрерывную зависимость от угловой координаты, необходимо выполнение равенства:
| (11) |
где 
Решением уравнения (11) являются функции sin n a и cos n a. Выбор той или иной из этих функций безразличен в силу симметрии волновода по угловой координате. Переход от одной функции к другой просто говорит о смене поляризации волны.
Левая часть уравнения (10) с учетом (11) принимает вид:
| (12) |
Это уравнение называется уравнением Бесселя. Его общее решение имеет вид:
| (13) |
где Jn (c r) - функция Бесселя (цилиндрическая функция 1-го рода); Yn (c r) - функция Неймана (цилиндрическая функция 2-го рода).
Поскольку 
второе решение в (13) отбрасываем (конечные источники не могут создавать бесконечные поля).
На рис. 2 представлены графики этих функций. Наибольший интерес представляют те значения аргумента, при которых обращаются в нуль либо сами функции Бесселя, либо их производные. Обозначим: hnq - q - й корень уравнения 
й корень уравнения 
Рис. 2
Значения корней функции Бесселя и корней производной функции Бесселя приведены в табл. 1,2.
Табл. 1
