Алгоритмы обхода в глубину и по уровням

Алгоритмы

1) Сортировка вставками

Сортировка вставками - достаточно простой алгоритм сортировки. Соответственно уступающий в производительности более сложным. Временная сложность данного алгоритма составляет О(n*n).

Описание алгоритма:
Идея алгоритма проста. На каждом из n - 1 (n - количество элементов в сортируемом массиве) шагов алгоритма выбирается какой-то элемент массива и затем вставляется на нужное место среди уже отсортированных элементов.
В стандартной реализации алгоритма присутствуют два цикла, один основной и другой вложенный. Основной цикл совершает n итераций, где n - количество элементов массива. Задачей основного цикла является выбор элемента массива, который необходимо вставить на нужное место. Во вложенном цикле происходит "протаскивание" выбранного элемента наверх, до тех пор пока не встретится элемент, который меньше выбранного.
Алгоритм состоит из следующих шагов:
1. Выбирается счетчик i = 1 (нет смысла брать i = 0, так как он итак является самым верхним элементом, и тащить его просто некуда)
2. Если i >= n, то конец алгоритма, иначе:
3. В переменную temp запоминается элемент A[i]: temp = A[i].
4. Выбирается счетчик j = i - 1.
5. Если j >= 0 и A[j] > temp, то происходит замещение элемента A[j + 1] на A[j], j уменьшается на единицу, и вновь выполняется шаг 5, в противном случае A[j + 1] замещается на значение temp, увеличивается i на 1 и выполняются шаги 2 - 5.

Иными словами, в переменную temp запоминается значение выбранного элемента (i - го на i - м шаге алгоритма), а далее происходит сдвиг всех элементов слева от выбранного, которые больше этого элемента на 1 позицию вправо. И после сдвига выбранный элемент, значение которого хранится в переменной temp, встает на освободившееся место в массиве.

Пример работы алгоритма:
Пусть дана последовательность А из 5 элементов, необходимо упорядочить её по возрастанию:

1. i = 1.
2. 1 >= 5 - ложь
3. temp = A[1] = 5.
4. j = 0.
5. 0 >= 0 - правда, A[0] = 6 > temp = 5 - правда, следовательно:
A[1] = A[0] = 6 и j = -1.
-1 > = 0 - ложь, следовательно:
A[0] = temp и i = 2.

6. 2 >= 5 - ложь
7. temp = A[2] = 2.
8. j = 1.
9. 1 >= 0 - правда, A[1] = 6 > temp = 2 - правда, следовательно:
A[2] = A[1] = 6 и j = 0.
0 >= 0 - правда, A[0] = 5 > temp = 2 - правда, следовательно:
A[1] = A[0] и j = -1.
-1 >= 0 - ложь, следовательно:
A[0] = temp i = 3.

... и так далее, до конца массива...

2) Сортировка выбором[ML1]

Сортировка выбором один из самых простых методов сортировки. Однако достаточно неэффективный.

У данной сортировки есть две разновидности. В одном случае мин. элемент меняется местами с первым и т. д. (как и описано далее), а в другом мин. элемент вырезается и вставляется в начало и т. д.

Описание алгоритма:
Пусть дана последовательность А из n элементов, нумерация элементов начинается с 0 (То есть первый элемент последовательности - A[0], второй - A[1], n-ый элемент A[n-1].) Необходимо упорядочить эту последовательность по возрастанию (по убыванию).
Сортировка выбором состоит из следующих шагов:
1. Кладется счетчик i равный 0.
2. Среди элементов последовательности от A[i] до A[n - 1] ищется минимальный элемент (максимальный элемент).
3. Меняются местами элемент A[i] и найденный на предыдущем шаге.
4. Счетчик i увеличивается на единицу.
5. Если i < n - 1, то повторяются шаги 2 - 5, в противном случае - конец алгоритма.

Пример работы алгоритма:
Пусть дана последовательность А из 5 элементов, необходимо упорядочить её по возрастанию:

1. Кладем счетчик i = 0.
2. Среди элементов от А[0] до A[4] ищем минимальный элемент.

3. Меняем местами элементы А[0] и A[4].

4. Увеличиваем счетчик i на 1. i = 1.
5. 1 < 4, переходим ко второму шагу алгоритма.
6. Среди элементов от А[1] до A[4] ищем минимальный элемент.

7. Меняем местами элементы А[1] и A[2].

8. Увеличиваем счетчик i на 1. i = 2.
9. 2 < 4, переходим ко второму шагу алгоритма.
10. Среди элементов от A[2] до A[4] ищем минимальный элемент.

11. Меняем местами элементы А[2] и A[2].

12. Увеличиваем счетчик i на 1. i = 3.
13. 3 < 4, переходим ко второму шагу алгоритма.
14. Среди элементов от А[3] до A[4] ищем минимальный элемент.

15. Меняем местами элементы А[3] и А[4].

16. Увеличиваем i на 1. i = 4.
17. 4 < 4, конец алгоритма.

Как видите, мы получили последовательность, упорядоченную по возрастанию элементов. Для получения последовательности, упорядоченной по убыванию элементов, необходимо искать максимальный, а не минимальный элемент на втором шаге алгоритма.

3) Пузырьковая сортировка Она же сортировка обменом

Сортировка пузырьком - очень простой и соответственно малоэффективный алгоритм сортировки. Свое название алгоритм получил за так называемое "всплытие легких элементов", подобно пузырькам в воде. Отметим, что сортировка пузырьком является устойчивой, то есть сохраняет порядок следования равных элементов.

Описание алгоритма:
Пусть имеется последовательность А из n элементов, которую необходимо упорядочить по возрастанию (по убыванию) элементов. Нумерация элементов последовательности начинается с 0 и заканчивается n - 1.
Сортировка пузырьком состоит из следующих шагов:
1. Выбирается переменная-счетчик i = 0.
2. Если i >= n, то конец алгоритма.
3. Выбирается переменная-счетчик j = n - 1.
4. Проверяются соседние элементы a[j] и a[j-1]. Если a[j] меньше a[j - 1] (то есть элемент ниже, легче элемента выше), то элементы меняются местами (происходит "всплытие" более легкого элемента).
5. Уменьшается переменная-счетчик j на 1.
6. Если j > i, то повторяются шаги 4 - 5. В противном случае переменная-счетчик i увеличивается на 1 и повторяются шаги 2 - 5.

Иными словами алгоритм состоит из двух циклов: основного и вложенного.
Основной цикл совершает n итераций. А во вложенном цикле происходит n - i (где i - номер итерации основного цикла) итераций. Проверка элементов во вложенном цикле начинается с конца массива, и если находится элемент, который легче предыдущего, то они меняются местами. Таким образом на первой итерации основного цикла самый легкий элемент последовательности "всплывает" на первое место, на второй итерации самый легкий элемент (не учитывая первый) "всплывает" на второе место и так далее.
Замечание: если необходимо упорядочить последовательность по убыванию, то необходимо изменить проверку с меньше на больше, и производить "всплытие тяжелых элементов".

Пример работы алгоритма:
Пусть дана последовательность А из 5 элементов, необходимо упорядочить её по возрастанию:

1. Кладем счетчик i = 0.
2. i = 0 < 5 - правда.
3. Кладем счетчик j = 5 - 1 = 4.
4. Проверяем элементы a[4] и a[3]. a[4] < a[3] следовательно меняем их местами.

5. Уменьшаем j на 1. j = 3.
6. j = 3 > 0, следовательно повторяем шаги 4 - 5 алгоритма.
... Выполняем шаги 3 - 5 пока j > i...

7. j = 0 > 0 - ложь, следовательно увеличиваем i = 1 и выполняем шаги 2 - 5.
8. i = 1 < 5 - правда.
9. Кладем счетчик j = 5 - 1 = 4.
10. Проверяем элементы a[4] и a[3]. a[4] > a[3] следовательно замены не происходит.
11. Уменьшаем j на 1. j = 3.
12. j = 3 > 1, следовательно повторяем шаги 4 - 5 алгоритма.
13. Проверяем элементы a[3] и a[2]. a[3] < a[2] следовательно меняем их местами.

... и так далее, в результате получаем упорядоченную по возрастанию последовательность А...

4) Пирамидальная сортировка[ML2]

Сортировка кучей или пирамидальная сортировка(англ HeapSort) является сортировкой, основанной на сравнениях. Эта сортировка обладет следующими свойствами:

§ нерекурсивная

§ нестабильная (т.е. не сохраняет исходный порядок данных с одинаковым ключом)

§ является асимптотически нормальной(т.е. работает за оптимальное для сортировки время -- O(n log n)), однако не очень быстрая в серднем случае и на отсортированных или почти отсортированных данных)

Алгоритм основан на одном из свойств кучи -- в голове(или вершине) кучи находится самый максимальный элемент.

Алгоритм

§ Построим из требуемого массива кучу

§ Меняем местами первый и последний элемент в куче

§ Уменьшаем размер рассматриваемой кучи на 1

§ Вызвать процедуру нормализации кучи(heapify) в корне кучи

§ Вернуться в шаг 2 и продолжать выполнять алгоритм, пока куча имеет больше одного элемента

Так как heapyfy работает за O(log n), а функция вызывается столько, сколько элементов массиве, то асимптотическая сложность алгоритма будет составлять O(n log n). Однако, на всех вариантах, даже на полностью отсортированном массиве, время работы алгоритма будет максимальным. Именно поэтому сортировка кучей не используется в стандартных пакетах.

5) Бинарный поиск

Совершенно очевидно, что других способов убыстрения поиска не существует, если, конечно, нет еще какой-либо информации о данных, среди которых идет поиск. Хорошо известно, что поиск можно сделать значительно более эффективным, если данные будут упорядочены. Поэтому приведем алгоритм (он называется ⌠поиском делением пополам■), основанный на знании того, что массив A отсортирован, т. е. удовлетворяет условию

Сначала нужно проверить – входит ли вообще элемент, который мы ищем в предложенный массив. Для этого элемент должен быть больше левого края массива и, соответственно, меньше правого.

Основная идея √ выбрать случайно некоторый элемент, предположим am, и сравнить его с аргументом поиска x. Если он равен x, то поиск заканчивается, если он меньше x, то делается вывод, что все элементы с индексами, меньшими или равными m, можно исключить из дальнейшего поиска; если же он больше x, то исключаются индексы больше и равные m. Выбор m совершенно не влияет на корректность алгоритма, но влияет на его эффективность. Очевидно, что чем большее количество элементов исключается на каждом шаге алгоритма, тем этот алгоритм эффективнее. Оптимальным решением будет выбор среднего элемента, так как при этом в любом случае будет исключаться половина массива. Пояснение: сравниваем наш элемент со средним в массиве, если наш элемент больше среднего элемента, то логично, что далее поиск нужно осуществлять только в правой части массива, если меньше – то только в левой. Дальнейший поиск, соответственно, осуществляется таким же делением подмассива пополам (сравнением с его средним элементом).

Рис.2.1. Поиск делением пополам

В этом алгоритме используются две индексные переменные L и R, которые отмечают соответственно левый и правый конец секции массива a, где еще может быть обнаружен требуемый элемент.

Алгоритм 2.

L:=0; R:=N-1; Found:=false;

while(L<=R) and not Found do begin

m:=(L+R) div 2;

if a[m]=x then begin

Found:=true

end else begin

if a[m]<x then L:=m+1 else R:=m-1

end

end;

Максимальное число сравнений для этого алгоритма равно log2n, округленному до ближайшего целого. Таким образом, приведенный алгоритм существенно выигрывает по сравнению с линейным поиском, ведь там ожидаемое число сравнений √ N/2.

Эффективность несколько улучшается, если поменять местами заголовки условных операторов. Проверку на равенство можно выполнять во вторую очередь, так как она встречается лишь единожды и приводит к окончанию работы. Но более существенный выигрыш даст отказ от окончания поиска при фиксации совпадения. На первый взгляд это кажется странным, однако, при внимательном рассмотрении обнаруживается, что выигрыш в эффективности на каждом шаге превосходит потери от сравнения с несколькими дополнительными элементами (число шагов в худшем случае равно logN).

Алгоритм 2▓.

L:=0; R:=N;

while L<R do begin

m:=(L+R) div 2;

if а[m]<x then L:=m+1 else R:=m

end

Окончание цикла гарантировано. Это объясняется следующим. В начале каждого шага L<R. Для среднего арифметического m справедливо условие L face="Symbol" =< m < R. Следовательно, разность L-R действительно убывает, ведь либо L увеличивается при присваивании ему значения m+1, либо R уменьшается при присваивании значения m. При L face="Symbol" =< R повторение цикла заканчивается.

Выполнение условия L=R еще не свидетельствует о нахождении требуемого элемента. Здесь требуется дополнительная проверка. Также, необходимо учитывать, что элемент a[R] в сравнениях никогда не участвует. Следовательно, и здесь необходима дополнительная проверка на равенство a[R]=x. Следует отметить, что эти проверки выполняются однократно.

Приведенный алгоритм, как и в случае линейного поиска, находит совпадающий элемент с наименьшим индексом.

 

6) Быстрая сортировка

Быстрая сортировка(Quick Sort, QSort) - сортировка, основанная на сравнениях, широко используется на практике из-за быстрой работы в большинстве случаев. Эта сортировка не является стабильной, реализуется рекурсивно. В худшем случае работает за .
Главное, что нужно понимать:

Выбираем опорный элемент p (средний).

Ищем слева от него элемент i с большим значением (именно большим, равные нас не интересуют). Как только находим, останавливаем перебор левой части.

Справа ищем элемент j с меньшим значением (равные также не интересуют). Как только находим, меняем найденный слева элемент i с найденным справа j местами.

Поиск элементов осуществляется до тех пор пока i <= j.

 

На входе массив a[0]...a[N] и опорный элемент p, по которому будет производиться разделение. Введем два указателя: i и j. В начале алгоритма они указывают, соответственно, на левый и правый конец последовательности. Будем двигать указатель i с шагом в 1 элемент по направлению к концу массива, пока не будет найден элемент a[i] >= p. Затем аналогичным образом начнем двигать указатель j от конца массива к началу, пока не будет найден a[j] <= p. Далее, если i <= j, меняем a[i] и a[j] местами и продолжаем двигать i,j по тем же правилам... Повторяем шаг 3, пока i <= j. Рассмотрим работу процедуры для массива a[0]...a[6] и опорного элемента p = a[3]. 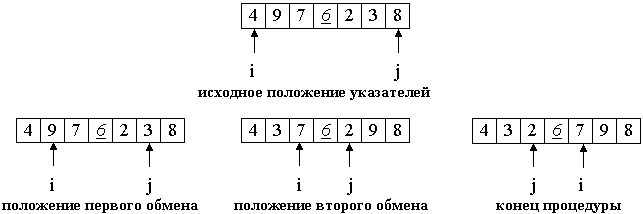Теперь массив разделен на две части: все элементы левой меньше либо равны p, все элементы правой - больше, либо равны p. Разделение завершено. На входе массив a[0]...a[N] и опорный элемент p, по которому будет производиться разделение. Введем два указателя: i и j. В начале алгоритма они указывают, соответственно, на левый и правый конец последовательности. Будем двигать указатель i с шагом в 1 элемент по направлению к концу массива, пока не будет найден элемент a[i] >= p. Затем аналогичным образом начнем двигать указатель j от конца массива к началу, пока не будет найден a[j] <= p. Далее, если i <= j, меняем a[i] и a[j] местами и продолжаем двигать i,j по тем же правилам... Повторяем шаг 3, пока i <= j. Рассмотрим работу процедуры для массива a[0]...a[6] и опорного элемента p = a[3]. Теперь массив разделен на две части: все элементы левой меньше либо равны p, все элементы правой - больше, либо равны p. Разделение завершено. Общий алгоритм } Реализация на Си. template<class T> void quickSortR(T* a, long N) { // На входе - массив a[], a[N] - его последний элемент. long i = 0, j = N; // поставить указатели на исходные места T temp, p; p = a[ N>>1 ]; // центральный элемент // процедура разделения do { while (a[i] < p) i++; while (a[j] > p) j--; if (i <= j) { temp = a[i]; a[i] = a[j]; a[j] = temp; i++; j--; } } while (i<=j); // рекурсивные вызовы, если есть, что сортировать if (j > 0) quickSortR(a, j); if (N > i) quickSortR(a+i, N-i); }

Общий алгоритм Псевдокод. quickSort (массив a, верхняя граница N) { Выбрать опорный элемент p - середину массива Разделить массив по этому элементу Если подмассив слева от p содержит более одного элемента, вызвать quickSort для него. Если подмассив справа от p содержит более одного элемента, вызвать quickSort для него. } Реализация на Си. template<class T> void quickSortR(T* a, long N) { // На входе - массив a[], a[N] - его последний элемент. long i = 0, j = N; // поставить указатели на исходные места T temp, p; p = a[ N>>1 ]; // центральный элемент // процедура разделения do { while (a[i] < p) i++; while (a[j] > p) j--;   if (i <= j) { temp = a[i]; a[i] = a[j]; a[j] = temp; i++; j--; } } while (i<=j); // рекурсивные вызовы, если есть, что сортировать if (j > 0) quickSortR(a, j); if (N > i) quickSortR(a+i, N-i); }

7) Кнута Мориса Пратта[ML3]

 

Алгоритм Кнута-Морриса-Пратта [ML4]

При построении конечного автомата для поиска подстроки в тексте легко построить переходы из начального состояния в конечное принимающее состояние: эти переходы помечены символами подстроки (см. рис. 1). Проблема возникает при попытке добавить другие символы, которые не переводят в конечное состояние.

Алгоритм Кнута-Морриса-Пратта основан на принципе конечного автомата, однако он использует более простой метод обработки неподходящих символов. В этом алгоритме состояния помечаются символами, совпадение с которыми должно в данный момент произойти. Из каждого состояния имеется два перехода: один соответствует успешному сравнению, другой - несовпадению. Успешное сравнение переводит нас в следующий узел автомата, а в случае несовпадения мы попадем в предыдущий узел, отвечающий образцу. Пример автомата Кнута-Морриса-Пратта для подстроки ababcb приведен на рисунке 2.

При всяком переходе по успешному сравнению в конечном автомате Кнутта-Морриса-Пратта происходит выборка нового символа из текста. Переходы, отвечающие неудачному сравнению, не приводят к выборке нового символа; вместо этого они повторно используют последний выбранный символ. Если мы перешли в конечное состояния, то это означает, что искомая подстрока найдена. Проверьте текст abababcbab на автомате, изображенном на рисунке 3, и посмотрите, как происходит успешный поиск подстроки.
Вот полный алгоритм поиска:

subLoc = 1 // указатель текущего сравниваемого символа в подстроке

textLoc = 1 // указатель текущего сравниваемого символа в тексте

 

while textLoc <= length(text) and subLoc <= length(substring) do

if subLoc = 0 or text[textLoc] = substring[subLoc] then

textLoc = textLoc + 1

subLoc = subLoc + 1

else // совпадения нет; переход по несовпадению

subLoc = fail[subLoc]

end if

end while

 

if (subLoc > length(substring)) then

return textLoc - length(substring) + 1 //найденное совпадение

else

return 0 // искомая подстрока не найдена

end if

 

Прежде, чем перейти к анализу этого процесса, рассмотрим как задаются переходы по несовпадению. Заметим, что при совпадении ничего особенного делать не надо: происходит переход к следующему узлу. Напротив, переходы по несовпадению определяются тем, как искомая подстрока соотносится сама с собой. Например, при поиске подстроки ababcb нет необходимости возвращаться назад на четыре позиции при необнаружении символа c. Если уж мы добрались до пятого символа в образце, то мы знаем, что первые четыре символа совпали, и поэтому символы ab в тексте, отвечающие третьему и четвертому символам образца, совпадают также с первым и вторым символами образца. Вот как выглядит алгоритм, задающий эти соотношения в подстроке:

fail[1] = 0

for i = 2 to length(substring) do

temp = fail[i - 1]

while (temp > 0) and (substring[temp] /= substring[i - 1]) do

temp = fail[temp]

end while

fail[i] = temp + 1

end for

 

8) Боена мура

 

Алгоритм Бойера-Мура

 

Сначала строится таблица смещений для каждого символа. Затем исходная строка и шаблон совмещаются по началу, сравнение ведется по последнему символу. Если последние символы совпадают, то сравнение идет по предпоследнему символу и так далее. Если же символы не совпали, то шаблон смещается вправо, на число позиций взятое из таблицы смещений для символа из исходной строки, и тогда снова сравниваются последние символы исходной строки и шаблона. И так далее, пока не шаблон полностью не совпадет с подстрокой исходной строки, или не будет достигнут конец строки.

Величина сдвига в случае несовпадения последнего символа вычисляется, исходя из следующего:

1. Сдвиг подстроки должен быть минимальным, таким, чтобы не пропустить вхождение подстроки в строке. Если данный символ строки встречается в подстроке, то смещаем подстроку таким образом, чтобы символ строки совпал с самым правым вхождением этого символа в подстроке. 2. Если же подстрока вообще не содержит этого символа, то сдвигаем подстроку на величину, равную ее длине, так что первый символ подстроки накладывается на следующий за проверявшимся символом строки.

 

Таблица смещений

Таблица смещений строится по принципу «пропускать столько символов, сколько возможно, но не более этого». Например, если на каком-то шаге алгоритма последние символы не совпали, и символ, находящийся в исходной строке не присутствует в шаблоне вообще, то понятно, что можно сдвинуться вправо на полную длину шаблона, без каких-либо опасений. В общем случае, каждому символу ставится в соответствие величина, равная разности длины шаблона и порядкового номера символа (если символ повторяется, то берется самое правое вхождение). Ясно, что эта величина будет в точности равна порядковому номеру символа, если считать от конца строки, что и дает возможность смещаться вправо на максимально возможное число позиций.

Иллюстрация

Чтобы стало совсем понятно рассмотрим работу алгоритма на примере:
Пусть исходная строка равна «somestring» и шаблон равен «string». Теперь строим таблицу смещений, она будет равна длине шаблона для всех символов, которые не встречаются в шаблоне, и порядковому номеру с конца для остальных (кроме последнего, для него тоже берется длина шаблона):

s->5
t->4
r->3
i->2
n->1
g->5

Теперь совмещаем наши строки:
somestring
string

Сравниваем последние символы: видим, что «t» не равен «g». Берем значение смещения для символа «t», оно равен 4. Сдвигаем строку вправо на 4 позиции, и вуаля:

somestring
string

Далее алгоритм будет сравнивать символы, от последнего и до первого в шаблоне с соответствующими символами в исходной строке. Как только он сравнит последний, то будет выяснено, что это и есть первое вхождение.

Графы

С формальной точки зрения граф представляет собой упорядоченную пару G = (V, Е) множеств, первое из которых состоит из вершин, или узлов, графа, а второе - из его ребер. Ребро связывает между собой две вершины. При работе с графами нас часто интересует, как проложить путь из ребер от одной вершины графа к другой. Поэтому мы будем говорить о движении по ребру; это означает, что мы переходим из вершины А графа в другую вершину В, связанную с ней ребром АВ (ребро графа, связывающее две вершины, для краткости обозначается этой парой вершин). В этом случае мы говорим, что А примыкает к В, или что эти две вершины соседние.
Граф может быть ориентированным или нет. Ребра неориентированного графа, чаще всего называемого просто графом, можно проходить в обоих направлениях. В этом случае ребро - это неупорядоченная пара вершин, его концов. В ориентированном графе, или орграфе, ребра представляют собой упорядоченные пары вершин: первая вершина - это начало ребра, а вторая - его конец. Далее мы для краткости будем говорить просто о ребрах, а ориентированы они или нет будет понятно из контекста.
Позже мы будем просто рисовать графы, а не задавать их множествами. Вершины будут изображаться кружочками, а ребра - отрезками линий. Внутри кружочков будут записаны метки вершин. Ребра ориентированного графа будут снабжены стрелками, указывающими допустимое направление движения по ребру.
На рисунке 1 изображено графическое представление неориентированного (а) и ориентированного (б) графов вместе с их формальным описанием.

 

 

Терминология
Полный граф - это граф, в котором каждая вершина соединена со всеми остальными. Числ ребер в полном графе без петель с N вершинами равно (N² - N)/2. В полном ориентирвоанном графе разрешается переход из любой вершины в любую другую. Поскольку в графе переход по ребру разрешается в обоих направлениях, а переход по ребру в орграфе - только в одном, в полном орграфе в два раза больше ребер, то есть их число равно N² - N.
Подграф (V_S, E_S) графа или орграфа (V, E) состоит из некоторого подмножества вершин и некоторого подмножества ребер, их соединяющих.
Путь в графе или орграфе - это последовательность ребер, по которым можно поочередно проходить. Другими словами, путь из вершины A в вершину B начинается в A и проходит по набору ребер до тех пор, пока не будет достигнута вершина B. С формальной точки зрения, путь из вершины v_i в вершину v_j это последовательность ребер графа v_iv_i+1, v_i+1v_i+2,..., v_j-1v_j. Мы требуем, чтобы любая вершина встречалась на таком пути не более, чем однажды. У всякого пути есть длина - число ребер в нем. Длина пути AB, BC, CD, DE равна 4.
Во взвешенном графе или орграфе каждому ребру приписано число, называемое весом ребра. При изображении графа обычно записывают вес ребра рядом с ребром. При формальном описании вес будет дополнительным элементом неупорядоченной или упорядоченной пары вершин (образуя вместе с этой парой "триплет"). При работе с ориентированными графами мы считаем вес ребра ценой прохода по нему. Стоимость пути по взвешенному графу равна сумме весов ребер пути. Кратчайший путь во взвешенном графе - это путь с минимальным весом, даже если число ребер в пути и можно уменьшить. Если, например, путь P₁ состоит из пяти ребер с общим весом 24, а путь P₂ - из трех ребер с общим весом 36, то путь P₁считается более коротким.
Граф или орграф называется связным, если всякую пару узлов можно соединить по крайней мере одним путем. Цикл - это путь, который начинается и кончается в одной и той же вершине. В ациклическом графе или орграфе циклы отсутствуют. Связный ациклический граф называется (неукорененным) деревом. Структура неукорененного дерева такая же, что и у дерева, только в нем не выделен корень. Однако каждая вершина неукорененного дерева может служить его корнем.

Алгоритмы обхода в глубину и по уровням

При работе с графами часто приходится выполнять некоторое действие по одному разу с каждой из вершин графа. Например, некоторую порцию информации следует передать каждому из компьютеров в сети. При этом мы не хотим посещать какой-либо компьютер дважды. Аналогичная ситуация возникает, если мы хотим собрать информацию, а не распространить ее.
Подобный обход можно совершать двумя различными способами. При обходе в глубину проход по выбранному пути осуществляется настолько глубоко, насколько это возможно, а при обходе по уровням мы равномерно двигаемся вдоль всех возможных направлений. Изучим теперь эти два способа более подробно. В обоих случаях мы выбираем одну из вершин графа в качестве отправной точки. Ниже под "посещением узла" мы понимаем выполнение действия, которое необходимо совершить в каждой вершине. Если, например, идет поиск, то фраза о том, что мы посетили данный узел, означает, что мы проверили его на наличие требуемой информации. Описываемые методы работают без каких-либо изменений как на ориентированных, так и на неориентированных графах. Мы будем иллюстрировать их на неориентированных графах.
С помощью любого из этих методов можно проверить, связен ли рассматриваемый граф. При обходе графа можно составить список пройденных узлов, а по завершении обхода составленный список можно сравнить со списком всех узлов графа. Если списки содержат одни и те же элементы, то граф связен. В противном случае в графе есть вершины, до которых нельзя дойти из начальной вершины, поэтому он несвязен.

Обход в глубину
При обходе в глубину мы посещаем первый узел, а затем идем вдоль ребер графа, пока не упремся в тупик. Узел неориентированного графа является тупиком, если мы уже посетили все примыкающие к нему узлы. В ориентированном графе тупиком также оказывается узел, из которого нет выходящих ребер.
После попадания в тупик мы возвращаемся назад вдоль пройденного пути пока не обнаружим вершину, у которой есть еще не посещенный сосед, а затем двигаемся в этом новом направлении. Процесс оказывается завершенным, когда мы вернулись в отправную точку, а все примыкающие к ней вершины уже оказались посещенными.
Иллюстрируя этот и другие алгоритмы обхода, при выборе одной из двух вершин мы всегда будем выбирать вершину с меньшей (в числовом или лексикографическом порядке) меткой. При реализации алгоритма выбор будет определяться способом хранения ребер графа.
Рассмотрим граф с рис. 1. Начав обход в глубину в вершине 1, мы затем посетим последовательно вершины 2, 3, 4, 7, 5 и 6 и упремся в тупик. Затем нам придется вернуться в вершину 7 и обнаружить, что вершина 8 осталась непосещенной. Однако, перейдя в эту вершину, мы немедленно вновь оказываемся в тупике. Вернувшись в вершину 4, мы обнаруживаем, что непосещенной осталась вершина 9; ее посещение вновь заводит нас в тупик. Мы снова возвращаемся назад в исходную вершину, и поскольку все соседние с ней вершины оказались посещенными, обход закончен.

Вот как выглядит рекурсивный алгоритм обхода в глубину:

DepthFirstTraversal (G, v)

G граф

v текущий узел

Visit(v)

Mark(v)

for каждого ребра vw графа G do

if вершина w непомечена then

DepthFirstTraversal(G, w)

End if

End for

 

Этот рекурсивный алгоритм использует системный стек для отслеживания текущей вершины графа, что позволяет правильно осуществить возвращение, наткнувшись на тупик. Вы можете построить аналогичный нерекурсивный алгоритм самостоятельно, воспользовавшись стеком для занесения туда и удаления пройденных вершин графа.

Обход по уровням
При обходе по уровням мы, после посещения первого узла, посещаем все соседние с ним вершины. При втором проходе посещаются все вершины "на расстоянии двух ребер" от начальной. При каждом новом проходе обходятся вершины, расстояние от которых до начальной на единицу больше предыдущего. В графе могут быть циклы, поэтому не исключено, что одну и ту же вершину можно соединить с начальной двумя различными путями. Мы обойдем эту вершину впервые, дойдя до нее по самому короткому пути, и посещать ее второй раз нет необходимости. Поэтому, чтобы предупредить повторное посещение, нам придется либо вести список посещенных вершин, либо занести в каждой вершине флажок, указывающий, посещали мы ее уже или нет.
Вернемся к графу с рис. 4. Начав обход с вершины 1, на первом проходе мы посетим вершины 2 и 8. На втором проходе на нашем пути окажутся вершины 3 и 7. (Вершины 2 и 8 также соединены с исходной вершиной путями длины два, однако мы не вернемся в них, поскольку уже побывали там при первом проходе.) При третьем проходе мы обойдем вершины 4 и 5, а при последнем - вершины 6 и 9.
В основе обхода в глубину лежала стековая структура данных, а при обходе по уровням мы воспользуемся очередью. Вот как выглядит алгоритм обхода по уровням:

BreadthFirstTraversal (G, v)

G граф

v текущий узел

Visit(v)

Mark(v)

Enqueue(v)

while очередь непуста do

Dequeue(x)

for каждого ребра xw в графе G do

if вершина w непомечена then

Visit(w)

Mark(w)

Enqueue(w)

End if

End for

End while

 

Этот алгоритм заносит в очередь корень дерева обхода по уровням, но затем немедленно удаляет его из очереди. При просмотре соседних с корнем вершин он заносит их в очередь. После посещения всех соседних с корнем вершин происходит возвращение к очереди и обращение к первой вершине оттуда. Обратите внимание на то, что поскольку узлы добавляются к концу очереди, ни одна из вершин, находящихся на расстоянии двух ребер от корня, не будет рассмотрена повторно, пока не будут обработаны и удалены из очереди все вершины на расстоянии одного ребра от корня.

[ML1]У данной сортировки есть две разновидности. В одном случае мин. элемент меняется местами с первым и т. д. (как и описано далее), а в другом мин. элемент вырезается и вставляется в начало и т. д. По крайнее мере так отображено на слайдах препода - http://vk.com/photo-33407561_296337607 и http://vk.com/photo-33407561_296337609.

[ML2]Насколько мне известно, это нам не нужно

[ML3]Сначала нужно рассмотреть прямой поиск - http://vk.com/photo-33407561_296337753 и http://vk.com/photo-33407561_296337805.

[ML4]Сам алгоритм я так толком и не понял J Главное отличие от прямого поиска в том, что смещение может происходить сразу на несколько элементов, а не на один. А вот как точно рассчитывается это смещение, не знаю …