Задание к выполнению работы. 1) Ознакомиться с приемами и теоретическими принципами работы в МК

1) Ознакомиться с приемами и теоретическими принципами работы в МК.

2) Создать документ в МК (имя файла: фамилия и номер группы исполнителя). Произвести вычисление 3-х выражений с использованием неповторяющихся математических операций.

3) Ввести 5 ранжированных переменных.

4) Задать 5 неповторяющихся функций одной переменной без использования ранжированных переменных и 5 векторов с их использованием.

5) Вывести функции на двумерные графики. Изменить параметры графиков с использованием системы координат, типа представления данных, масштаба, цвета, характера линий, а также различных маркеров.

Задание для самостоятельной работы

1) Задать 5 неповторяющихся функций двух переменных без использования ранжированных переменных и 5 матриц с их использованием.

2) Вывести функции на трехмерные графики. Изменить параметры графиков с использованием типа масштаба, цвета, характера линий, а также различных маркеров.

3) Задать наименование графиков и сформировать легенду. Создать комментарии к выполняемым заданиям в виде текстовых блоков.

Требования к отчету

Отчет должен содержать:

– Титульную страницу с данными об исполнителе и проверяющем.

– Тему, цель работы, порядковый номер и номер варианта.

– Краткие теоретические сведения.

– Макет документа МК, выполненный согласно варианта.

– Выводы о проделанной работе.

Отчет должен быть оформлен согласно требованиям ГОСТ.

Лабораторная работа №2

ПРИБЛИЖЕННОЕ РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Цель работы: получить навыки нахождения приближенного решения уравнений средствами МК

Теоретические сведения

2.1.1 Функция поиска корня нелинейного уравнения – root

Многие уравнения, не имеют аналитических решений. Однако они могут решаться численными методами с заданной погрешностью. Для простейших уравнений вида F (x) =0 решение находится с помощью функции rооt. Синтаксис ее применения выглядит следующим образом:

Rооt(Выражение, Имя_переменной)=.

Например:

Rооt(x²-2x+1, x)=.

Эта функция возвращает значение переменной, при которой выражение равно 0 с заданной точностью. Функция реализует вычисления итерационным методом, причем можно задать начальное значение переменной. Это особенно полезно, если возможно несколько решений. Тогда выбор решения определяется выбором начального значения переменной.

Как известно, кубическое уравнение обязательно имеет хотя бы один действительный корень х1. Два других корня могут оказаться и комплексными. Функция root позволяет найти как действительные так и комплексные корни. Для поиска второго корня х2 первый исключается делением F (x) на (x-x1). Соответственно для поиска третьего корня x З F (x) делится еще и на (х-х2). Эту процедуру можно распространить и на поиск корней полиномов более высокой степени.

2.1.1 Директива Given для решения системы уравнений

При решении систем линейных и нелинейных уравнений используется специальный вычислительный блок, открываемый служебным словом Given – и имеющий следующую структуру:

«Начальные условия»

Given

«Уравнения»

«Ограничительные условия»

«Выражения с функциями Find, Minerr, Maximize и Minimize»

Начальные условия определяют начальные значения искомых переменных. Они задаются обычным присваиванием переменным заданных значений.

Уравнения задаются в виде expr_left = expr_right с применением жирного знака равенства «=» между левой и правой частью каждого уравнения.

Ограничительные условия обычно задают в виде неравенств или равенств, которые должны удовлетворяться при вычислении системы уравнений.

2.1.2 Функции Find и Minerr для решения систем нелинейных уравнений

Команда Find(v1, v2, …, vn) = – возвращает значение одной или нескольких переменных для точного решения, а команда Minerr(v1, v2, …, vn) = – возвращает значение одной или нескольких переменных для приближенного решения.

Между этими функциями существуют принципиальные различия. Первая функция используется, когда решение реально существует (хотя и считается аналитическим). Вторая функция пытается найти максимальное приближение даже к несуществующему решению путем минимизации среднеквадратичной погрешности решения.

Функции Find и Minerr могут использоваться для решения одного или ряда уравнений. Следует помнить, что использование знака присваивания вместо знака символического (логического) равенства в блоке Given некорректно. Поэтому система реагирует на попытку решения сообщением об ошибке.

Так же можно решать и другие задачи. Например, поиск точек пересечения параболы и прямой. В данном случае с помощью функции Find решается система из двух уравнений (одно из них нелинейное) с ограничительными условиями, задающими область поиска корня (y<0 для отрицательного корня и y>0 для положительного корня).

При использовании функции Minerr для решения систем нелинейных уравнений надо проявлять осторожность и обязательно предусматривать проверку решений. Нередки случаи, когда решения могут оказаться ошибочными, чаще всего из-за того, что из нескольких корней система предлагает нереальный (или не представляющий интереса) корень. Поэтому необходимо как можно точнее указывать начальные приближения к решению.

2.1.3 Решение дифференциальных уравнений

Известно, что далеко не всегда удается найти решение дифференциального уравнения. Поэтому разработаны методы для их приближенного решения. Имеется большое количество таких методов. Здесь будут рассмотрены лишь некоторые из них.

Метод Эйлера

Найдем приближенно решение уравнения у ' = f (х, у) в точках х₁ = х₀+h, х_n = х₀+nh при начальном условии:

y(х₀) = y₀,

где h – постоянный шаг.

Обозначим y(x_k) = у_k. Учитывая, что

,

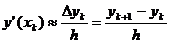заданное уравнение запишем так:

.

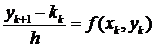Отсюда

y_k+1 = y_k+hf (x_k,y_k).

Полагая в этой формуле k = 0,1,2,... находим последовательно величины у₁, y₂ …

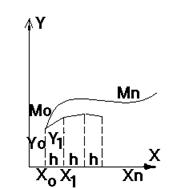
Рисунок 2.1 – Метод Эйлера

По этим данным построим ломаную Эйлера,·которая приближенно заменяет интегральную кривую, проходящую через точку M₀(x₀, y₀) (рис. 2.1).

Геометрически метод Эйлера означает, что через точку M₀(x₀, y₀) проводим не интегральную кривую, а касательную к ней, которую и принимаем приближенно за интегральную кривую на участке от x₀ до x₁=x₀+h. После этого за исходную точку берем M₁(x₁, y₁) и поступаем так же, как и до этого.

Метод Эйлера прост, но точность его невелика. Если интервал { х₀, х }, где ищется решение, разбит на n частей h= (x-x₀) /n, то погрешность при вычислении ординат имеет порядок 1/h. Это означает, что для повышения точности в 10 раз (получения одного дополнительного десятичного знака) требуется увеличить число точек деления в десять раз. Последнее значительно увеличит объем вычислений.

Метод Рунге-Кутта

Пусть у_k – приближенное значение решения при x = x_k уже построено.

Найдем:

f_k=f (x_k, y_k),

a_k=f (x_k+h/2, y_k+f_kh/2),

и за приближенное значение решения при х = х_k+1 = x_k + h примем:

y_k+1 = y_k + a_kh.

Рисунок 2.2 – Метод Рунге-Кутта

Геометрически это означает, что для построения звена М_k М_k+1 ломаной, аппроксимирующей интегральную кривую, сначала проводим через точку М отрезок Μ_k Μ_k+1, совпадающий с направлением f_k поля в точке М_k (как это делалось в методе Эйлера). Вычисляем координаты точки N_k – середины этого отрезка:

(х_к+h/2, y_k+h/2),

и находим величину

a_k=f (x_k+h/2, y_k+f_kh/2).

Через точку М_k проводим отрмок M_k M_k+\ параллельно направлению поля в точке N_k. Ординату точки M_k+1 и принимаем за у_k+1.

Этот метод будет точнее метода Эйлера, так как он учитывает поворот поля на интервале { x_k, x_k+1 }.

Еще более точный результат получим, если вычисления про­водить по схеме:

f_k=f (x_k, y_k),

a_k=f (x_k+h/2, y_k+f_nh/2),

b_k=f (x_k+h/2, y_k+a_nh/2),

g_k=f (x_k+h/2, y_k+b_nh),

y_k+1=y_k+1/6 (f_k+2a_k+2b_k+g_k) h.

За исходную точку, как и раньше, берем точку m₀ (х₀,y₀). Выбрав шаг А, вычислим:

F₀=f (x₀, y₀),

a₀=f (x₀+h/2, y₀+f₀h/2),

b₀=f (x₀+h/2, y₀+a₀h/2),

g₀=f (x₀+h/2, y₀+b₀h).

Находим

y₁=y₀+1/6 (f₀+2a₀+2b₀+g₀) h.

Получили точку Μ₁ (x₁, y₁). Аналогично находим f₁, a₁, b₁, g₁ и вычисляем у₂ и так далее.

2.1.4 Функции решения дифференциальных уравнений

Рассмотрим пример использования функции Rkfixed, предназначенной для поиска набора значений решения дифференциального уравнения методом Рунге-Кутта, встроенной в МК.

Синтаксис применения функций для решения данной задачи выглядит следующим образом: