Связь вектора напряженности электрического поля с потенциалом. Эквипотенциальные поверхности

Электрическое поле можно описать либо с помощью векторной величины напряженности электрического поля E, либо с помощью скалярной величины φ.

Связь между напряженностью поля и его потенциалом

Сила связана с напряженностью

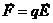, потенциальная энергия связана с потенциалом 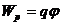, сила связана с потенциальной энергией , следовательно, и .- это соотношение устанавливает связь между напряженностью и потенциалом. Т. о. По известным значениям потенциала можно найти значение напряженности поля. Можно решить и обратную задачу, по заданным значениям напряженности в каждой точке найти разность потенциала между двумя произвольными точками поля.

Это следует из формул для работы , также работа может быть вычислена по формуле . Приравнивая друг к другу эти выражения и сократив на q. Получим соотношение .

Воображаемая поверхность все точки которой имеют одинаковый потенциал, называются эквипотенциальной поверхностью. Ее уравнение имеет вид . При перемещении по эквипотенциальной поверхности на отрезок dl потенциал не изменится (). Так как проекция вектора напряженности на произвольное направление равна , то следовательно касательная к поверхности составляющая вектор напряженности E, равна нулю.

Отсюда заключаем, что вектор напряженности в каждой точке направлен по нормали к эквипотенциальной поверхности, проходящей через данную точку, а линии напряженности в каждой точке ортогональны эквипотенциальной поверхностям. Эквипотенциальную поверхность можно провести через любую точку поля и следовательно таких поверхностей можно построить бесконечное множество., Условились проводить поверхности таким образом чтобы разность потенциалов для двух соседних поверхностей была всюду одной и той же. Тогда по густоте эквипотенциальных поверхностей можно судить о величине напряженности поля. Для однородного поля эквипотенциальные поверхности представляют собой систему одинаково отстоящих друг от друга плоскостей перпендикулярных к направлению поля.