Все тела в природе способны электризоваться, т.е. приобретать электрический заряд. Наличие электрического заряда проявляется в том, что заряженное тело взаимодействует с другими заряженными телами. Имеются 2 вида электрических зарядов, условно называемых положительными и отрицательными. Заряды одного знака отталкиваются, заряды разных знаков притягиваются. Электрический заряд является свойством некоторых элементарных чатиц, например электрон имеет отрицательный заряд –e, протон – положительный заряд +e, нейтрон – заряд равный нулю. Заряд элементарных частиц одинаковый по величине и называется элементарным зарядом
Электрические заряды входят в состав атомов и молекул любого вещества. Обычно частицы, несущие отрицательный и положительный заряды присутствуют в веществе в одинаковом количестве (молекула нейтральна). Если создать избыток положительно заряженных частиц в теле, то тело станет положительно заряженным (положительно заряженный ион), и наоборот, если отрицательно заряженных частиц больше, то будем иметь отрицательно заряженное тело (отрицательный ион).
|
|
|
В 1785 году Кулон экспериментально установил закон взаимодействия точечных зарядов. Точечным зарядом называется заряженное тело, размерами которого можно пренебречь по сравнению с расстояниями от этого тела до других тел, несущих электрический заряд. Кулон с помощью крутильных весов измерял силу взаимодействия двух заряженных шариков в зависимости от величины зарядов на них и от расстояния между ними.Закон: Сила взаимодействия двух неподвижных точечных зарядов пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними. Направление силы совпадает с направлением прямой соединяющей заряды.
 . k – коэффициент пропорциональности, предполагается положительным,
. k – коэффициент пропорциональности, предполагается положительным,  - единичный вектор, имеющий направление от одного заряда к другому.
- единичный вектор, имеющий направление от одного заряда к другому.
Если имеется система зарядов: заряд qa и еще n зарядов, то равнодействующая сила с которой действует заряд qa определяется формулой 
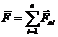
 - сила с которой действует на заряд qa заряд qi в отсутствие остальных n-1 зарядов. Таким образом можно вычислить силу взаимодействия между зарядами сосредоточенными на телах конечных размеров, для этого надо разбить каждый из зарядов на малые заряды, которые можно считать точенными, найти силу взаимодействия между всеми точенными зарядами взятыми попарно и найти векторную сумму этих сил.
- сила с которой действует на заряд qa заряд qi в отсутствие остальных n-1 зарядов. Таким образом можно вычислить силу взаимодействия между зарядами сосредоточенными на телах конечных размеров, для этого надо разбить каждый из зарядов на малые заряды, которые можно считать точенными, найти силу взаимодействия между всеми точенными зарядами взятыми попарно и найти векторную сумму этих сил.
В симтеме единиц СГСЭ (абсолютная электростатическая система единиц: грамм, см, секунда, для заряда – СГСЭ абсолютная электростатическая единица заряда k=1 и закон кулона имеет вид  .В системе СИ заряд измеряется в Кулонах опытным путем установили, что 1Кл =2.998 * 109 единиц заряда СГСЭ. Элементарный заряд выраженный в Кулонах равен e= 1.60* 10-19Кл.
.В системе СИ заряд измеряется в Кулонах опытным путем установили, что 1Кл =2.998 * 109 единиц заряда СГСЭ. Элементарный заряд выраженный в Кулонах равен e= 1.60* 10-19Кл.
|
|
|
В системе единиц СИ коэффициент пропорциональности в законе Кулона равен 
 - электростатическая постоянная = 0.885 *10-11Ф/м (Фарада/метр).
- электростатическая постоянная = 0.885 *10-11Ф/м (Фарада/метр).
Напряженность электростатического поля
Всякий заряд изменяет свойства окружающего его пространства – создает в нем электрическое поле. Это поле проявляется в том, что помещенный в какую-либо его точку
Электрический заряд испытывает воздействие силы. Взаимодействие между заряждами осуществляется через электрическое поле. Будем вносить пробные заряды в поле неподвижного точечного заряда и измеряя силы, действующие на пробный заряд было установлено что отношение 
 для всех пробных зарядов остается постоянным и зависит только от q и r, определяющих поле в данной точке.
для всех пробных зарядов остается постоянным и зависит только от q и r, определяющих поле в данной точке.
Величину  , характеризующую электрическое поле называют напряженностью электрического поля в данной точке пространства.
, характеризующую электрическое поле называют напряженностью электрического поля в данной точке пространства. 
Направление вектора напряженности E – вдоль радиальной прямой, проходящей через заряд и данную точку поля, от заряда, если он положителен, и к заряду, если он отрицателен
Принцип суперпозиции электрических полей. Напряженность электрического поля, создаваемая системой точечных зарядов, непрерывным распределением зарядов. Поле диполя, бесконечной прямолинейной однородно заряженной нити.
Напряженность электростатического поля
Всякий заряд изменяет свойства окружающего его пространства – создает в нем электрическое поле. Это поле проявляется в том, что помещенный в какую-либо его точку
Электрический заряд испытывает воздействие силы. Взаимодействие между заряждами осуществляется через электрическое поле. Будем вносить пробные заряды в поле неподвижного точечного заряда и измеряя силы, действующие на пробный заряд было установлено что отношение 
 для всех пробных зарядов остается постоянным и зависит только от q и r, определяющих поле в данной точке. Величину
для всех пробных зарядов остается постоянным и зависит только от q и r, определяющих поле в данной точке. Величину  , характеризующую электрическое поле называют напряженностью электрического поля в данной точке пространства.
, характеризующую электрическое поле называют напряженностью электрического поля в данной точке пространства.
 Направление вектора напряженности E – вдоль радиальной прямой, проходящей через заряд и данную точку поля, от заряда, если он положителен, и к заряду, если он отрицателен.
Направление вектора напряженности E – вдоль радиальной прямой, проходящей через заряд и данную точку поля, от заряда, если он положителен, и к заряду, если он отрицателен.
На всякий точечный заряд q в точке поля с напряженностью E будет действовать сила 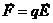 . В случае отрицательного q направления векторов
. В случае отрицательного q направления векторов 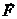 и
и  совпадают. В случае отрицательного q направления векторов
совпадают. В случае отрицательного q направления векторов 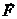 и
и  противоположны. Так как сила с которой система зарядов действует на заряд не входящий в эту систему зарядов, равна векторной сумме сил, с которыми действуют на данный заряд каждый из зарядов системы в отдельности, вытекает принцип суперпозиции (наложения) электрических полей: напряженность поля системы зарядов равна векторной сумме напряженностей полей, которые создал бы каждый из зарядов в отдельности
противоположны. Так как сила с которой система зарядов действует на заряд не входящий в эту систему зарядов, равна векторной сумме сил, с которыми действуют на данный заряд каждый из зарядов системы в отдельности, вытекает принцип суперпозиции (наложения) электрических полей: напряженность поля системы зарядов равна векторной сумме напряженностей полей, которые создал бы каждый из зарядов в отдельности 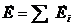 .
.
Напряженность электрического поля от нескольких зарядов находится по правилу векторного сложения полей.
Принцип суперпозиции позволяет вычислять напряженность поля любой системы зарядов. Разбив протяженные заряды на достаточно малые доли, любую систему можно свести к совокупности точечных зарядов.
Напряженность поля, образованного заряженной бесконечно протяженной плоскостью
 , где σ – поверхностная плотность заряда на плоскости.
, где σ – поверхностная плотность заряда на плоскости.
Напряженность поля, образованного бесконечно длинной нитью
 где τ– линейная плотность заряда на нити α расстояние от нити. Диполем называется система двух разноименных зарядов одинаковых по величине +q и –q, расстояние l между которыми значительно меньше расстояния до тех точек системы, в которых определяется поле системы. Прямая, проходящая через оба заряда, называется осью диполя.
где τ– линейная плотность заряда на нити α расстояние от нити. Диполем называется система двух разноименных зарядов одинаковых по величине +q и –q, расстояние l между которыми значительно меньше расстояния до тех точек системы, в которых определяется поле системы. Прямая, проходящая через оба заряда, называется осью диполя.
|
|
|
 , p =q l – характеристика диполя – электрический момент pn =pcosθ. Положив θ=0, получим напряженность поля на оси диполя
, p =q l – характеристика диполя – электрический момент pn =pcosθ. Положив θ=0, получим напряженность поля на оси диполя
 направлен по оси диполя.
направлен по оси диполя.
Положив θ=π/.2, получим напряженность поля на оси диполя
 параллелен оси диполя.
параллелен оси диполя.
Характерным для напряженности поля является то обстоятельство, что она убывает с расстоянием от диполя как  , т.е. быстрее чем напряженность поля точечного заряда.
, т.е. быстрее чем напряженность поля точечного заряда.
Силовые линии напряженности электрического поля. Поток вектора напряженности электрического поля. Теорема Остроградского-Гаусса, примеры ее применения (поле, создаваемое однородной бесконечной плоскостью).
Электрическое поле можно описывать, указав для каждой точки величину и направление вектора E. Электрическое поле можно описать с помощью линий напряженности электрического поля. Линии напряженности проводят таким образом, чтобы касательная к ним в каждой точке совпадала с направлением вектора E. Густота линий выбирается таким образом, чтобы количество линий, пронизывающих единицу поверхности, перпендикулярной к линиям площадки, было равна числовому значению вектора E. Тогда по картине линий вектора E можно судитьо величине и направлении напряженности в разных точках пространства.
Поток вектора.
Величина  - поток вектора через поверхность. Поток вектора – это алгебраическая величина, знак которой зависит от выбор направления нормали к элементарной площадке, на которые разбивается поверхность S.
- поток вектора через поверхность. Поток вектора – это алгебраическая величина, знак которой зависит от выбор направления нормали к элементарной площадке, на которые разбивается поверхность S.
В случае замкнутых поверхностей принято вычислять поток «вытекающий» наружу, следовательно нормаль всегда подразумевается направленная наружу (внешняя нормаль).
Дивергенцией называется величина  . Интеграл берется по произвольной замкнутой поверхности S, окружающей точку, V – объем ограниченный этой поверхностью. Так как поток через замкнутую поверхность определяется по формуле
. Интеграл берется по произвольной замкнутой поверхности S, окружающей точку, V – объем ограниченный этой поверхностью. Так как поток через замкнутую поверхность определяется по формуле 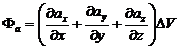 ,
,
то разделив это выражение на  , найдем дивергенцию вектора a в точке P
, найдем дивергенцию вектора a в точке P 
 .
.
Зная дивергенцию вектора в каждой точке пространства, можно вычислить поток этого вектора через любую замкнутую поверхность конечных размеров. Соотношение  называется теоремой Остроградского-Гаусса. Интеграл в левой части вычисляется по произвольной замкнутой поверхности, в правой части – по объему, ограниченному этой поверхностью.
называется теоремой Остроградского-Гаусса. Интеграл в левой части вычисляется по произвольной замкнутой поверхности, в правой части – по объему, ограниченному этой поверхностью.
|
|
|
Силы, действующие на заряд q являются консервативными, т.е. работа этих сил на любом замкнутом контуре равна нулю:
 . Сократив на q получим соотношение. Интеграл, стоящий в левой части представляет собой циркуляцию вектора по контуру Г. Т.о. циркуляция вектора напряженности по любому замкнутому контуру равна нулю. Возьмем произвольную поверхность, опирающуюся на контур Г, для которого вычисляется циркуляция. Согласно теореме Стокса (
. Сократив на q получим соотношение. Интеграл, стоящий в левой части представляет собой циркуляцию вектора по контуру Г. Т.о. циркуляция вектора напряженности по любому замкнутому контуру равна нулю. Возьмем произвольную поверхность, опирающуюся на контур Г, для которого вычисляется циркуляция. Согласно теореме Стокса (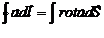 ) интеграл от ротора Е, взятый по этой поверхности, равен циркуляции вектора Е по контуру Г:
) интеграл от ротора Е, взятый по этой поверхности, равен циркуляции вектора Е по контуру Г:
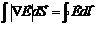 , т.к. циркуляция равна нулю, получим
, т.к. циркуляция равна нулю, получим 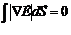 , т.о. ротор вектора Е в каждой точке поля равен нулю
, т.о. ротор вектора Е в каждой точке поля равен нулю  .Следовательно электростатическое поле безвихревое.
.Следовательно электростатическое поле безвихревое.
Теорема Гаусса
Поток вектора E равен  . Знак потока совпадает со знаком заряда. Допустим, что внутри замкнутой поверхности находится n точечных зарядов. В силу принципа суперпозиции напряженность E, создаваемая всеми зарядами, равна сумме напряженностей, создаваемых каждым зарядом в отдельности. Поэтому
. Знак потока совпадает со знаком заряда. Допустим, что внутри замкнутой поверхности находится n точечных зарядов. В силу принципа суперпозиции напряженность E, создаваемая всеми зарядами, равна сумме напряженностей, создаваемых каждым зарядом в отдельности. Поэтому
 - теорема Гаусса: ток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме зарядов, делен на
- теорема Гаусса: ток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме зарядов, делен на  . При рассмотрении полей, создаваемых макроскопическими зарядами, отвлекаются от дискретной структуры этих зарядов и считают их распределенными в пространстве непрерывным образом с конечной всюду плотностью. Объемная плотность заряда ρ определяется по формуле
. При рассмотрении полей, создаваемых макроскопическими зарядами, отвлекаются от дискретной структуры этих зарядов и считают их распределенными в пространстве непрерывным образом с конечной всюду плотностью. Объемная плотность заряда ρ определяется по формуле  . В данном случае физически малый объем должен быть мал, чтобы плотность была одинаковой, но и не слишком мал, чтобы не появилась дискретность заряда. Зная плотность заряда в каждой точке пространства, можно вычислить суммарный заряд
. В данном случае физически малый объем должен быть мал, чтобы плотность была одинаковой, но и не слишком мал, чтобы не появилась дискретность заряда. Зная плотность заряда в каждой точке пространства, можно вычислить суммарный заряд

 заменяя поверхностный интеграл объемным, получим
заменяя поверхностный интеграл объемным, получим  . И следовательно дивергенция вектора напряженности связана с плотностью заряда в той же точке равенством
. И следовательно дивергенция вектора напряженности связана с плотностью заряда в той же точке равенством  . – теорема Гаусса в дифференциальной форме.
. – теорема Гаусса в дифференциальной форме.
Теорема Гаусса позволяет вычислять напряженность полей. Поверхностная плотность определяется по формуле  (если заряд сосредоточен в тонком поверхностном слое), линейная плотность
(если заряд сосредоточен в тонком поверхностном слое), линейная плотность  (если заряд равномерно распределен в каждом сечении).
(если заряд равномерно распределен в каждом сечении).
Поле бесконечной заряженной плоскости.
Пусть поверхностная плотность заряда во всех точках одинакова и равна σ. Будем считать заряд положительным. Из соображений симметрии вытекает, что напряженность поля в любой точке имеет направление перпендикулярное к плоскости.
Далее очевидно, что в симметричных относительно плоскости точках напряженность поля одинакова по величие и противоположна по направлению. Пусть цилиндрическая поверхность с образующими перпендикулярными к плоскости и основаниями величины 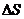 , расположенными относительно плоскости симметрично. Применим к поверхности теорему Гаусса. П через боковую поверхность равен нулю, т. к.
, расположенными относительно плоскости симметрично. Применим к поверхности теорему Гаусса. П через боковую поверхность равен нулю, т. к.  в каждой точке поверхности равен нулю. Для
в каждой точке поверхности равен нулю. Для  из которого следует
из которого следует  - напряженность поля бесконечной плоскости.
- напряженность поля бесконечной плоскости.
4. Работа сил электрического поля при перемещении заряда. Теорема о циркуляции вектора напряженности электростатического поля.
Рассмотрим поле, создаваемое неподвижным зарядом q. В любой точке этого поля на точечный заря действует сила Кулона 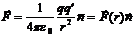 . Так как сила является центральной, поле этой силы консервативно. Следовательно работа, которую совершается силами поля над зарядом
. Так как сила является центральной, поле этой силы консервативно. Следовательно работа, которую совершается силами поля над зарядом  при перемещении из одной точки в другую не зависит от пути.
при перемещении из одной точки в другую не зависит от пути.
Работа равна  , dl – элементарное перемещение.
, dl – элементарное перемещение.  .
.  - потенциальная энергия. Работа консервативного поля может быть представлена как убыль потенциальной энергии.
- потенциальная энергия. Работа консервативного поля может быть представлена как убыль потенциальной энергии.  .
.
 и следовательно
и следовательно  .
.
Интеграл может быть взят по любой Лии, соединяющей точки 1 и 2. Для обхода по замкнутому контуру  , т.е.
, т.е. 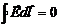 . Это соотношение справедливо только для электростатического поля.
. Это соотношение справедливо только для электростатического поля.
Силы, действующие на заряд q являются консервативными, т.е. работа этих сил на любом замкнутом контуре равна нулю:
 . Сократив на q получим соотношение. Интеграл, стоящий в левой части представляет собой циркуляцию вектора по контуру Г. Т.о. циркуляция вектора напряженности по любому замкнутому контуру равна нулю. Возьмем произвольную поверхность, опирающуюся на контур Г, для которого вычисляется циркуляция. Согласно теореме Стокса (
. Сократив на q получим соотношение. Интеграл, стоящий в левой части представляет собой циркуляцию вектора по контуру Г. Т.о. циркуляция вектора напряженности по любому замкнутому контуру равна нулю. Возьмем произвольную поверхность, опирающуюся на контур Г, для которого вычисляется циркуляция. Согласно теореме Стокса ( ) интеграл от ротора Е, взятый по этой поверхности, равен циркуляции вектора Е по контуру Г:
) интеграл от ротора Е, взятый по этой поверхности, равен циркуляции вектора Е по контуру Г:
 , т.к. циркуляция равна нулю, получим
, т.к. циркуляция равна нулю, получим 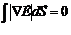 , т.о. ротор вектора Е в каждой точке поля равен нулю
, т.о. ротор вектора Е в каждой точке поля равен нулю  .Следовательно электростатическое поле безвихревое.
.Следовательно электростатическое поле безвихревое.
 2018-01-08
2018-01-08 2260
2260