Для любой дискретной СВ X – числовая функция F(x) = Р(Х < х),
-∞ < х < +∞ называется функцией распределения (ФР) этой СВ, а функция f(х) = F'(x), называется плотностью распределения или плотностью вероятности (ПВ) этой СВ.
Приведем графики возможных ФР F(x)и ПВ f(х)при равномерном законе распределения.
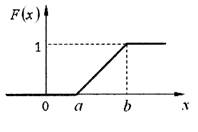
Рисунок 1 – Функция распределения при равномерном законе
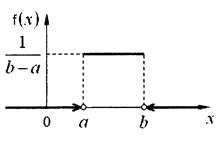
Рисунок 2 – Плотность вероятности при равномерном законе
ФР любой случайной величины обладает следующими свойствами:
F(x) определена на всей числовой прямой R;
F(x) не убывает, т.е. если x1 ≤ x2, то F(x1) ≤ F(x2);
F(-∞)=0, F(+∞)=1, т.е. 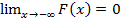 и
и 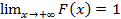
F(x) непрерывна справа, т.е.. 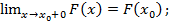
ПВ любой случайной величины обладает следующими свойствами:
плотность распределения – неотрицательная функция f(x) ≥ 0;
несобственный интеграл от плотности распределения в пределах от - ∞ до +∞ равен единице:
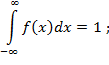
Рассмотрим основные числовые характеристики СП.
Математическое ожидание – мера среднего значения случайной величины, определяется формулой:
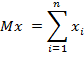
Дисперсия случайной величины – мера разброса данной случайной величины, то есть её отклонения от математического ожидания:
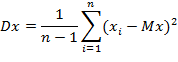
Абсолютны центральны момент k-го порядка СВ X:
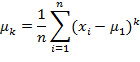
Коэффициент ассиметрии – числовая характеризующая степени несимметричности распределения СВ:
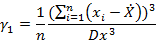
Коэффициент эксцесса – числовая характеризующая степени остроты пика распределения СВ:
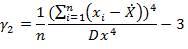
Для коэффициента ассиметрии и эксцесса Ẋ – среднее значение:
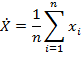
 2017-10-31
2017-10-31 422
422








