2018-01-08
2403
Вытекающая из теории Бора дискретная структура энергетических уровней электрона в атоме позволяет объяснить закономерности в спектре излучения атома водорода. Из опыта известно, что спектр теплового излучения невзаимодействующих атомов имеет дискретный характер в виде совокупности отдельных спектральных линий, которые определенным образом упорядочены в некоторые группы, называемые сериями. Такая сериальная упорядоченность спектра излучения атома водорода описывается обобщенной формулой Бальмера:
, где 
и 
- постоянные Ридберга: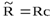 
,
n - номер спектральной серии; n = 1, 2, 3 …
m - номер спектральной линии в серии; m = n + 1, m + 2 …
При n = 1; n = 
(1 – 1/m2), где m = 2, 3, 4 … - серия Лаймана – лежит в ультрафиолетовом диапазоне.
n = 2; n = (1/22 – 1/m2), где m = 3, 4, 5… - серия Бальмера – первые четыре ее линии лежат в
видимой области спектра.
n
= 3;n= 
(1/32 – 1/m2), где m = 4, 5, 6 … - серия Пашена – лежит в инфракрасной области.
Наглядное представление механизма образования сериально упорядоченного линейчатого спектра атома водорода дано на схеме.
|
|
|
Теория Бора позволяет просто получить и саму обобщенную формулу Бальмера. Выразим из правила частот Бора 
частотуn излучения:
и, подставив в нее выражение для энергии: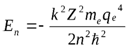 
получим: 
Сравнивая с формулой Бальмера, видим, что постоянная Ридберга образуется набором фундаментальных физических констант: 
при Z = 1. Подставляя их значения, получим для 
значение 
, совпадающее с известным из опыта.
Формулу Бальмера часто записывают не для частоты n, а для обратной длины волны 1/l.
Из n = с/lÞ 1/l = n/с = ( /с)(1/n2 – 1/m2) = R(1/n2 – 1/m2), где R = /с = 
.
Спектральная линия с наибольшей длиной волны в данной серии называется ее головной линией, а с наименьшей длиной волны – границей серии.
Формула Бальмера оказывается применимой для так называемых водородоподобных атомов. К ним относят ионизованные атомы, имеющие один электрон, например, однократно ионизованный атом гелия Не+(Z = 2) и двухкратно ионизованный атом лития Li++ (Z = 3).
