Расчет надежности восстанавливаемой системы с помощью интегральных уравнений

Рассмотрим методику составления интегрального уравнения для каждого состояния 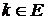. Сначала определяются все состояния, из которых имеется одношаговый переход в состояние k. Пусть j – одно из таких состояний, и переход из j в k вызван отказом или восстановлением элемента с номером 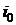. Обозначим через 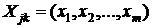вектор, в котором компо­ненты 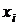принимают два значения: x (переменная интегрирования) или 0. Еcли в состоянии k элемент с номером i работает или восстанавливается, то 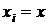. Если в состоянии k элемент с номером i находится в состоянии про­стоя, то .

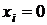Пусть для i -го элемента 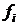есть плотность распределения времени безотказ­ной работы, если 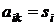, или плотность распределения времени восста­новления 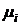, если 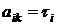. Тогда справедливо уравнение

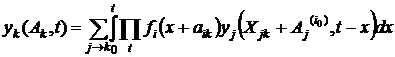. (6.6)

Суммирование в правой части производится по всем состояниям j, из которых имеется непосредственный переход в состояние k. Произведение под знаком интеграла распространяется на все индексы i, для которых вектор

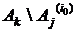имеет «ненулевые» компоненты. Для начального состояния 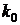к правой части соответствующего интегрального уравнения (6.6) добавляется cлагаемое

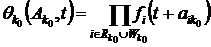, (6.7)

обусловленное началом функционирования системы.