КУРСОВАЯ РАБОТА
По теплотехнике
Выполнила:
студентка группы В-631
Коробанова София Владимировна
Проверил(а):
кандидат технических наук,
доцент
Чащинов Валерий Иванович
Брянская область 2017
Индивидуальное задание на курсовую работу по теплотехнике
(исходные данные для решения задач)
Студенту: Коробановой Софии Владимировне группы В- 631
Шифр задания 316
Задача 1
Состав смеси:
| № п/п | Компонент | Доля, % | Способ задания |
| Азот (N2) | объемный | ||
| Гелий (He) | |||
| Кислород (О2) |
Прочие данные:
| m, кг | t1, 0С | p1, МПа | V1, м3 |  0С 0С
| Процесс |
| 0,85 | - | изобарный |
Задача 2
 , 0С , 0С
| 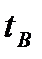 , 0С , 0С
|  ,Вт/м2К ,Вт/м2К
| 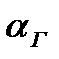 ,Вт /м2К ,Вт /м2К
|  , мм , мм
|  ,мм ,мм
|  , мм , мм
|  , мм , мм
|
| 0,8 | 7,5 | 3,5 | 0,2 |
Задача 3
| тв ,т/ч |  0 С 0 С
|  0 С 0 С
| l,м | d н, мм | δ, мм | ω, м/с |  , Вт /м2К , Вт /м2К
| pг, МПа |
| 15,2 | 2,1 | 2,0 | 1,1 | 0,28 |
Задание выдано _____ ____________ 20____г.
Преподаватель _____________/Чащинов В.И./
s cy8ucmVsc1BLAQItABQABgAIAAAAIQDIsPb3RgcAAABLAAAOAAAAAAAAAAAAAAAAAC4CAABkcnMv ZTJvRG9jLnhtbFBLAQItABQABgAIAAAAIQBICLAz4gAAAAwBAAAPAAAAAAAAAAAAAAAAAKAJAABk cnMvZG93bnJldi54bWxQSwUGAAAAAAQABADzAAAArwoAAAAA ">
| Лист |
| Изм. |
| Лист |
| № документа |
| Подпись |
| Дата |
Введение
1. Расчет термодинамической системы с газовыми смесями
1.1. Термодинамические процессы, задачи их расчета и анализа
1.2. Основные сведения о газовых смесях
Задача 1
2. Расчет процесса теплопередачи
2.1. Общие сведения о теплообмене
2.2. Теплопроводность
2.3. Конвективный теплообмен
2.4. Теплообмен излучением
2.5. Теплопередача
Задача 2
3. Расчет теплообменника
3.1. Общие сведения о теплообменниках
3.2. Основы расчета рекуперативных теплообменников
Задача 3
Литература
| Изм. |
| Лист |
| № докум. |
| Подп. |
| Дата |
| Лист |
| КРТТ ХХХ 000. 001 ПЗ |
| Разраб. |
| Коробанова С. В. |
| Провер. |
| Чащинов В.И |
| Н. Контр. |
| Утв. |
| Введение |
| Лит. |
| Листов |
| БГАУВ-631 |
Теплотехника является общетехнической дисциплиной, которая занимает одно из центральных мест в инженерной подготовке специалистов. Законы тепло- и массообмена в практике пожарного дела используются при научных исследованиях, связанных с оценкой пожаро- и взрывобезопасных параметров процессов нагрева, сушки, при определении огнестойкости строительных конструкций, пожароопасных свойств горючих материалов, эффективности огнетушащих средств и особенно при оценке основных факторов пожара внутри зданий – температуры и газообмена.
Курсовая работа выполняется в целях более глубокого изучения дисциплины «Теплотехника». Задание на курсовую работу содержит 100 вариантов. Вариант курсовой работы определяет преподаватель, а задания выбираются в соответствии со своим вариантом приведённой в начале каждой части курсовой работы.
| Лист |
| Изм. |
| Лист |
| № документа |
| Подпись |
| Дата |
Термодинамические процессы, задачи их расчета и анализа
Термодинамическим процессом называется любые изменения параметров состояния системы во времени.
Различают равновесные и неравновесные, обратимые и необратимые процессы.
Под равновесным понимают процесс, в ходе которого система проходит последовательность равновесных состояний. При этом равновесным считается состояние системы, когда во всех ее точках параметры состояния имеют одинаковые значения.
В противном случае мы имеем неравновесный процесс.
Обратимыми являются процессы, протекающие без рассеивания энергии. Для таких процессов, если изменить ход процесса на обратный, система пройдет те же состояния, как и при прямом течении процесса и может возвратиться в исходное состояние без каких-либо потерь энергии.
При необратимых процессах происходит рассеивание энергии и для возвращения системы в исходное состояние при таких процессах необходимы дополнительные затраты энергии.
Обратимыми могут быть только равновесные процессы. И хотя все реальные процессы являются необратимыми, обратимые процессы широко используются при анализе термодинамических систем, как модель, удобная для выявления основных закономерностей и получения во многих случаях количественных результатов с приемлемой точностью.
Обратимые термодинамические процессы могут графически изображаться в координатах р-v и Т-s.
При этом часто изображение процесса в координатах р-v называют рабочей диаграммой (площадь под графиком процесса в соответствующем масштабе равна работе за процесс), а изображение в координатах Т-s – тепловой диаграммой (площадь под графиком процесса равна теплоте в процессе).
Наиболее характерными и часто рассматриваемыми процессами в термодинамике являются изохорный (при постоянном объеме), изобарный (при постоянном давлении), изотермический (при постоянной температуре) и адиабатный (без теплообмена с внешней средой). Обратимый адиабатный процесс называют также изоэнтропийным, поскольку для него изменение энтропии – ds=0.
| Лист |
| Изм. |
| Лист |
| № документа |
| Подпись |
| Дата |
· установление соотношений между параметрами состояния в начале и в конце процесса;
· определение теплоты и работы в процессе;
· изменение функций состояния в процессе (внутренней энергии – ∆u, энтальпии – ∆i и энтропии – ∆s);
· графическое представление процесса в координатах p-v (рабочая диаграмма) и в координатах T-s (тепловая диаграмма).
При анализе термодинамических процессов используют уравнение процесса, которое выражает связь между параметрами состояния на любой момент в ходе процесса, первый закон термодинамики, общие выражения теплоты и работы в процессах.
Следует учитывать, что теплота в процессе считается положительной, если она подводится к системе, а работа считается положительной при расширении системы, т.е. когда она преодолевает сопротивление окружающей среды.
Уравнения процессов имеют вид:




В этих формулах приняты обозначения:
 – давление, Па;
– давление, Па;
 – удельный объем, м3/кг;
– удельный объем, м3/кг;
 – термодинамическая температура, К;
– термодинамическая температура, К;
k – показатель адиабаты.
Выражение первого закона термодинамики в конечной форме имеет вид
 , (3.5)
, (3.5)
где
 – количество удельной теплоты в процессе, Дж/кг;
– количество удельной теплоты в процессе, Дж/кг;
 – изменение внутренней энергии в процессе, Дж/кг;
– изменение внутренней энергии в процессе, Дж/кг;
 – удельная работа (работа расширения) в процессе, Дж/кг.
– удельная работа (работа расширения) в процессе, Дж/кг.
| Лист |
| Изм. |
| Лист |
| № документа |
| Подпись |
| Дата |
 , (3.6)
, (3.6)
где
 – удельная массовая теплоемкость в соответствующем процессе, Дж/кг˖К;
– удельная массовая теплоемкость в соответствующем процессе, Дж/кг˖К;
Изменение функций состояния в любых газовых процессах рассчитываются по формулам:
 ; (3.7)
; (3.7)
 ; (3.8)
; (3.8)

где
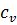 – удельная массовая изохорная теплоемкость, Дж/кг˖К;
– удельная массовая изохорная теплоемкость, Дж/кг˖К;
 – удельная массовая изобарная теплоемкость, Дж/кг˖К;
– удельная массовая изобарная теплоемкость, Дж/кг˖К;
 – удельная массовая теплоемкость в соответствующем процессе, Дж/кг˖К.
– удельная массовая теплоемкость в соответствующем процессе, Дж/кг˖К.
Индекс «1» соответствует началу процесса, а индекс «2» - его окончанию.
Множество термодинамических процессов объединяется понятием политропного процесса.
Политропным называется обобщающий термодинамический процесс, удовлетворяющий уравнению pvⁿ=const, для которого доля теплоты, идущая на изменение внутренней энергии, является величиной постоянной.
Здесь n – показатель политропы, постоянный для данного политропного процесса, и который в зависимости от характера процесса может принимать значения от -∞ до +∞.
При этом рассмотренные выше четыре основных процесса можно считать частными случаями политропного процесса при соответствующем значении показателя политропы: при n = ± ∞ имеем изохорный процесс, при n = 0 – изобарный, при n = 1 – изотермический и при n = k – адиабатный.
| Лист |
| Изм. |
| Лист |
| № документа |
| Подпись |
| Дата |

Между показателем политропы и характеристикой политропного процесса существуют следующие соотношения:
 ; (3.11)
; (3.11)
или  ; (3.12)
; (3.12)
Теплоемкость политропного процесса может быть найдена по формулам

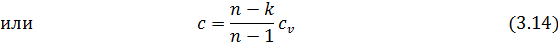
Исходя из уравнения процесса, соотношения между начальными и конечными параметрами политропного процесса имеют вид:
 ;
;  ;
; 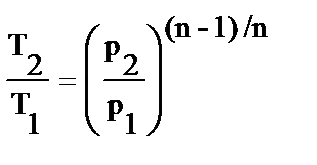 . (3.15)
. (3.15)
Удельная работа в политропном процессе
l =  (T1-T2)=
(T1-T2)=  (p1v1 – p2v2) =
(p1v1 – p2v2) = 
 . (3.16)
. (3.16)
1.2.
| Лист |
| Изм. |
| Лист |
| № документа |
| Подпись |
| Дата |
Часто рабочим телом в термодинамических системах используются газовые смеси. Такие системы рассчитываются так же, как и системы с однородным газом с учетом соответствующих характеристик газовой смеси, которые зависят от состава смеси.
Чтобы задать газовую смесьнеобходимо назвать компоненты смеси и указать долю каждого компонента в смеси. Состав смеси задают массовыми, объемными или молярными долями.
Массовой долейкомпонента  называют отношение массы i -го газа
называют отношение массы i -го газа  , входящего в смесь, к массе всей смеси
, входящего в смесь, к массе всей смеси 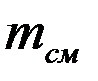
 =
=  /
/ 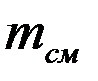 .
.
Объемной долейкомпонента  называют отношение приведенного объема i -го газа
называют отношение приведенного объема i -го газа  , входящего в смесь, к объему всей смеси
, входящего в смесь, к объему всей смеси 
 =
=  /
/  .
.
При этом приведенным объемомгаза называется объем, который занял бы один этот газ при температуре и давлении смеси.
Молярной долейкомпонента 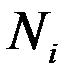 называют отношение количества киломолей i -го газа
называют отношение количества киломолей i -го газа 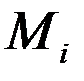 , входящего в смесь, к общему количеству киломолей смеси
, входящего в смесь, к общему количеству киломолей смеси 
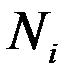 =
= 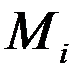 /
/  .
.
Для любой газовой смеси, состоящей из  компонентов, выполняется условие:
компонентов, выполняется условие: 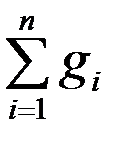 =
=  =
=  = 1.
= 1.
| Лист |
| Изм. |
| Лист |
| № документа |
| Подпись |
| Дата |
 =
=  ;
;  =
=  ;
;  =
= 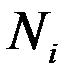 , (3.17)
, (3.17)
где:
 – молярная масса
– молярная масса  -го газа, входящего в смесь;
-го газа, входящего в смесь;
 – число компонентов, входящих в смесь.
– число компонентов, входящих в смесь.
Для газовых смесей вводится понятие парциального давления газа, входящего в смесь, под которым понимают часть общего давления смеси, создаваемую данным компонентом. То есть парциальное давлениегаза, входящего в смесь, – это давление, которое установилось бы в данном объеме, если из него удалить все другие компоненты смеси, при температуре смеси. Парциальное давление i -го газа может быть найдено по формуле
 =
=  . (3.18)
. (3.18)
При этом согласно закону Дальтонадавление смеси  равно сумме парциальных давлений ее компонентов
равно сумме парциальных давлений ее компонентов 
 =
=  .
.
Основные параметры смеси идеальных газов могут быть найдены из следующих соотношений.
Кажущаяся молярная масса смеси
 =
= 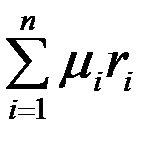 . (3.19)
. (3.19)
Плотность смеси
 =
= 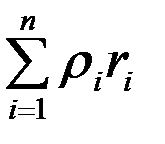 . (3.20)
. (3.20)
Газовая постоянная смеси
 =
=  (3.21)
(3.21)
| Лист |
| Изм. |
| Лист |
| № документа |
| Подпись |
| Дата |
 =
=  , Дж / кг К. (3.22)
, Дж / кг К. (3.22)
Удельная массовая теплоемкость смеси
 . (3.23)
. (3.23)
Удельная объемная теплоемкость смеси
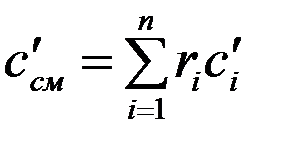 . (3.24)
. (3.24)
В этих формулах
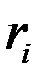 и
и  – соответственно объемная и массовая доля i -го компонента смеси;
– соответственно объемная и массовая доля i -го компонента смеси;
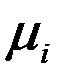 ,
, 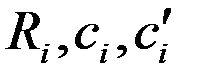 – соответственно молярная масса, газовая постоянная, удельные массовая и объемная теплоемкости
– соответственно молярная масса, газовая постоянная, удельные массовая и объемная теплоемкости  -го газа, входящего в смесь
-го газа, входящего в смесь
| Лист |
| Изм. |
| Лист |
| № документа |
| Подпись |
| Дата |
Выполнить расчет термодинамической системы, рабочим телом в которой является газовая смесь массой m= 8 кг следующего состава:
| № п/п | Компонент | Доля, % | Способ задания |
| Азот (N2) | объемный | ||
| Гелий (He) | |||
| Кислород (О2) |
В изобарном процессе температура смеси изменяется на величину  0 С при начальных условиях: t 1,= 30 0 С и p 1 = 0,85МПа.
0 С при начальных условиях: t 1,= 30 0 С и p 1 = 0,85МПа.
Требуется рассчитать массовые доли компонентов, найти все параметры состояния в начале и в конце процесса, а также изменение функций состояния, работу и количество теплоты в процессе. Представить процесс в p-V и T-S координатах. Расчеты выполнить, считая рабочее тело идеальным газом.
Решение
Из справочных таблиц выписываем основные характеристики компонентов газовой смеси: газовую постоянную, молярную массу и показатель адиабаты:
для азота – 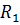 = 0,2968 кДж/кг˖К,
= 0,2968 кДж/кг˖К,  = 28 кг/кмоль,
= 28 кг/кмоль,  = 1,4;
= 1,4;
для гелия –  = 2,078 кДж/кг˖К,
= 2,078 кДж/кг˖К,  = 4 кг/кмоль,
= 4 кг/кмоль,  = 1,67;
= 1,67;
для кислорода –  = 0,2598 кДж/кг˖К,
= 0,2598 кДж/кг˖К,  = 32 кг/кмоль,
= 32 кг/кмоль,  = 1,4.
= 1,4.
1. Рассчитываем объемные доли компонентов с использованием формулы
 =
=  ; (П1.1)
; (П1.1)
где
 – объемная доля
– объемная доля  -го газа, входящего в смесь;
-го газа, входящего в смесь;
 – массовая доля
– массовая доля  -го газа, входящего в смесь;
-го газа, входящего в смесь;
| Лист |
| Изм. |
| Лист |
| № документа |
| Подпись |
| Дата |
 – молярная масса
– молярная масса  -го газа, входящего в смесь;
-го газа, входящего в смесь;
 – число компонентов, входящих в смесь.
– число компонентов, входящих в смесь.
Подставляя соответствующие данные в формулу (П1.1) получаем:
для азота – 
для гелия – 
для кислорода –  .
.
Правильность расчетов проверяем условием  = 1, которое в нашем случае выполняется: 0,237 + 0,719 + 0,044 = 1,0
= 1, которое в нашем случае выполняется: 0,237 + 0,719 + 0,044 = 1,0
2. Определяем основные характеристики газовой смеси.
Кажущаяся молярная масса смеси
 =
=  =28˖0,2968 + 32˖0,2598 + 4˖2,078 = 24,94 кг/кмоль.
=28˖0,2968 + 32˖0,2598 + 4˖2,078 = 24,94 кг/кмоль.
Газовая постоянная смеси
 =
=  = 0,2968˖0,6 + 2,078˖0,26 + 0,2598˖0,14 = 0,7546 кДж/кг˖К. В этой формуле
= 0,2968˖0,6 + 2,078˖0,26 + 0,2598˖0,14 = 0,7546 кДж/кг˖К. В этой формуле  – молярная масса
– молярная масса  -го газа, входящего в смесь.
-го газа, входящего в смесь.
Удельная массовая теплоемкость смеси рассчитывается по формуле
 , (П1.2)
, (П1.2)
где  – соответственно массовая доля и удельная массовая теплоемкость
– соответственно массовая доля и удельная массовая теплоемкость  -го газа, входящего в смесь.
-го газа, входящего в смесь.
При этом необходимо найти как изохорную  , так и изобарную
, так и изобарную  теплоемкость смеси, подставляя в формулу (П1.2) соответственно изохорные и изобарные теплоемкости компонентов смеси.
теплоемкость смеси, подставляя в формулу (П1.2) соответственно изохорные и изобарные теплоемкости компонентов смеси.
В свою очередь теплоемкости компонентов рассчитываются по формулам:

 , (П1.4)
, (П1.4)
| Лист |
| Изм. |
| Лист |
| № документа |
| Подпись |
| Дата |
где  – показатель адиабаты
– показатель адиабаты  -го компонента смеси.
-го компонента смеси.
Результаты расчета теплоемкости смеси представляем в табличной форме
Таблица П1.1 – Результаты расчета теплоемкости
| Компонентсмеси |  ,
кДж/ кг˖К ,
кДж/ кг˖К
| 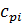 ,
кДж/ кг˖К ,
кДж/ кг˖К
|  ,
кДж/ кг˖К ,
кДж/ кг˖К
|  ,
кДж/ кг˖К ,
кДж/ кг˖К
|
| 1. Азот | 0,742 | 1,039 | 1,34252 | 2,09721 |
| 2. Гелий | 3,1015 | 5,17591 | ||
| 3. Кислород | 0,6495 | 0,909 |
 = 0,742*0,63+3,1015*0,26+0,6495*0,14=1,34252
= 0,742*0,63+3,1015*0,26+0,6495*0,14=1,34252
 =1,039*0,6+5,17905*0,26+0,909*0,14=2,09721
=1,039*0,6+5,17905*0,26+0,909*0,14=2,09721
Определяем параметры состояния в начале и в конце процесса.
К параметрам состояния относятся термодинамическая температура – T, давление – p и удельный объем – v.
В нашем случае начальная температура и давление заданы и составляют соответственно
 30 + 273 =303K и
30 + 273 =303K и  = 0,85 МПа.
= 0,85 МПа.
Удельный объем в начале процесса определим из уравнения состояния для 1 кг газа
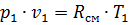 , (П1.5)
, (П1.5)
где
 – начальное давление, кПа;
– начальное давление, кПа;
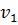 – начальный удельный объем, м3/кг;
– начальный удельный объем, м3/кг;
 – газовая постоянная смеси, кДж/ кг˖К;
– газовая постоянная смеси, кДж/ кг˖К;
 – начальная температура, К.
– начальная температура, К.

| Лист |
| Изм. |
| Лист |
| № документа |
| Подпись |
| Дата |
 8˖0,2698 = 2,1584 м3.
8˖0,2698 = 2,1584 м3.
Заданный в условии задачи изобарный процесс является процессом, протекающим при постоянном давлении. Поэтому давление в конце процесса
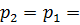 0,85 МПа.
0,85 МПа.
С учетом условия задачи температура в конце процесса будет равна
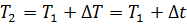 = 303 + 130 =433 К.
= 303 + 130 =433 К.
Удельный объем в конце процесса найдем по соотношению начальных и конечных параметров, вытекающего из уравнения изобарного процесса:

Соответственно объем смеси в конце процесса составит
 8˖0,3856 = 3,0849 м3.
8˖0,3856 = 3,0849 м3.
1. Рассчитаем количество теплоты, работу и изменение функций состояния в процессе.
Количество теплоты в изобарном процессе
 = 8˖2,09721˖130 = 2181,10 кДж.
= 8˖2,09721˖130 = 2181,10 кДж.
Работа в нашем процессе
 = 850(3,8561– 2,6984) = 984,045 кДж.
= 850(3,8561– 2,6984) = 984,045 кДж.
Изменение внутренней энергии
 .
.
Изменение энтальпии для изобарного процесса равно количеству теплоты в процессе, то есть
 = 2181,102 кДж.
= 2181,102 кДж.
Изменение энтропии рассчитываем по формуле

Полученные результаты расчёта процесса сведем в таблицу. При этом для построения графика процесса в координатах T-S примем значение S 1 = 0,5 кДж/К и определим положение промежуточной точки «a», для которой зададимся значением температуры  = 340 К.
= 340 К.
| Лист |
| Изм. |
| Лист |
| № документа |
| Подпись |
| Дата |
| Величина | p, МПа | T, К | v, м3/кг | V, м3 |  кДж кДж
| L, кДж |  кДж кДж
|  кДж кДж
|  кДж/К
кДж/К
|  кДж/К кДж/К
|
| Начало процесса (точка 1) | 0,85 | 2,6984 | 2,1587 | 2181,1 | 98406,2 | 1396,22 | 2181,1 | 5,989 | 0,5 | |
| Конец процесса (точка 2) | 0,85 | 3,8561 | 3,0849 | 3,034 |
Изменение энтропии  для промежуточной точки составляет
для промежуточной точки составляет

Соответственноэнтропия промежуточной точки

Рассчитанный процесс представлен на рис. П1.1 в координатах p-V и T-S.
На этом же рисунке изображены также изохорный (1-3), изотермический (1-4) процессы с подводом теплоты и адиабатный процесс расширения (1-5). При этом эти процессы представлены без расчета, исходящими из той же начальной точки, что и заданный процесс
Рис. П1.1. Графическое представление процессов
2.
| Лист |
| Изм. |
| Лист |
| № документа |
| Подпись |
| Дата |
 2018-01-21
2018-01-21 1756
1756







